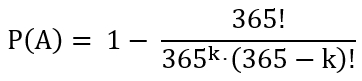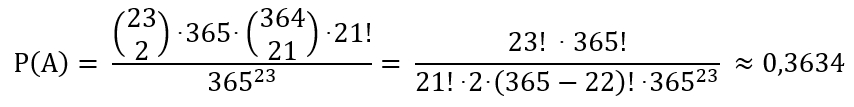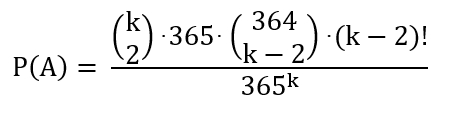Das Geburtstagsparadoxon

1. Fall:

In einem Zimmer befinden sich z.B. 23 Personen. Wie groß ist dann die Wahrscheinlichkeit, dass mindestens 2 Personen am gleichen Tag Geburtstag haben (Ereignis A)?
Es wird vorausgesetzt, dass die Geburtstage im Jahr mit 365 Tagen (kein Schaltjahr) gleich verteilt sind und sich keine Zwillingspaare (Drillingspaare usw.) darunter befinden.

Um diese Wahrscheinlichkeit P(A) zu berechnen geht man zunächst von der Gegenwahrscheinlichkeit (Wahrscheinlichkeit des Gegenereignisses) aus:
Wie groß ist die Wahrscheinlichkeit, dass keine 2 von 23 Personen am gleichen Tag Geburtstag haben, d.h. dass alle 23 Personen an verschiedenen Tagen Geburtstag haben?

Die (Laplace-)Wahrscheinlichkeit P(A) eines Ereignisses A erhält man, indem man die Anzahl |A| der für A günstigen Ergebnisse durch die Gesamtzahl m der möglichen Ergebnisse dividiert.

Entsprechendes gilt für das Gegenereignis , wobei gilt: 

Bei 2 Personen gilt: 

Bei 3 Personen gilt: 

. . .

Bei 23 Personen gilt: 

Damit gilt für die Wahrscheinlichkeit P(A):

Mit einer Wahrscheinlichkeit von ungefähr 50,7 % haben mindestens 2 von 23 Personen am gleichen Tag Geburtstag.

Das Ergebnis ist für viele Menschen verblüffend und wird deshalb als Paradoxon bezeichnet.

Allgemein gilt für die Wahrscheinlichkeit, dass mindestens 2 von k Personen am gleichen Tag Geburtstag haben:

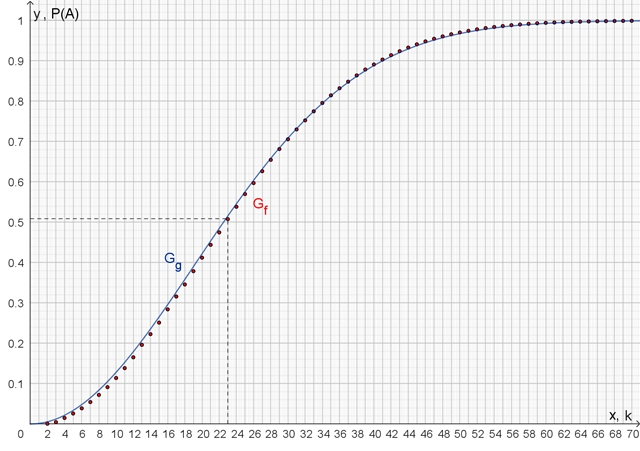
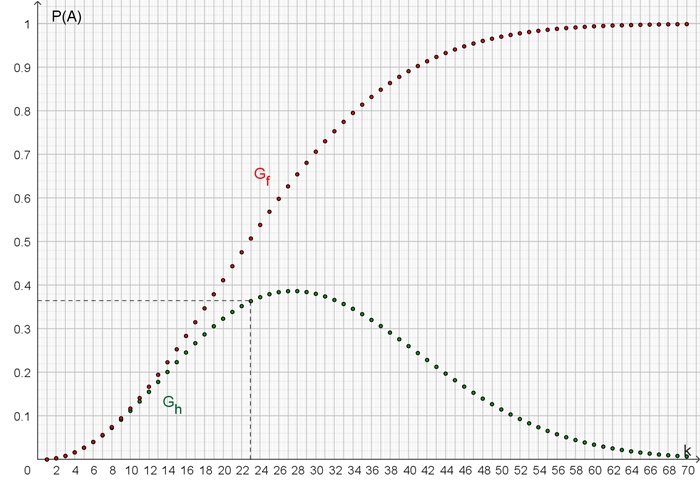
Grafische Darstellung G_f für die Wahrscheinlichkeit, dass mindestens 2 von k Personen am gleichen Tag Geburtstag haben

Näherung durch die Funktion mit der Gleichung 

2. Fall:

In einem Zimmer befinden sich z.B. 23 Personen. Wie groß ist dann die Wahrscheinlichkeit, dass genau 2 Personen am gleichen Tag Geburtstag haben (Ereignis A)?

Mit einer Wahrscheinlichkeit von ungefähr 36,3 % haben genau 2 von 23 Personen am gleichen Tag Geburtstag.

Allgemein gilt für die Wahrscheinlichkeit, dass genau 2 von k Personen am gleichen Tag Geburtstag haben:

Ab der Anzahl k = 28 von Personen wird wird es unwahrscheinlicher, dass genau 2 Personen (und nicht mehr Personen) am gleichen Tag Geburtstag haben.

Grafische Darstellung G_h für die Wahrscheinlichkeit, dass genau 2 von k Personen am gleichen Tag Geburtstag haben im Vergleich mit G_f

Das Wichteln-Paradoxon

Wichteln ist ein vorweihnachtlicher Brauch, bei dem sich Jugendliche in Jugendgruppen, in Schulklassen oder Arbeitskollegen gegenseitig beschenken. Dabei sollen die Geschenke gesammelt und dann zufällig verteilt werden.

Wie groß ist nun die Wahrscheinlichkeit, dass keine Person ihr eigenes Geschenk erhält?

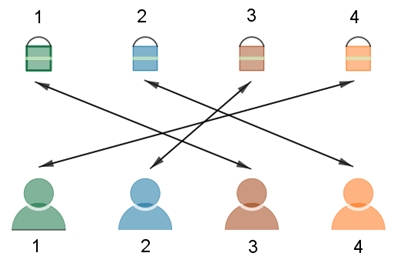
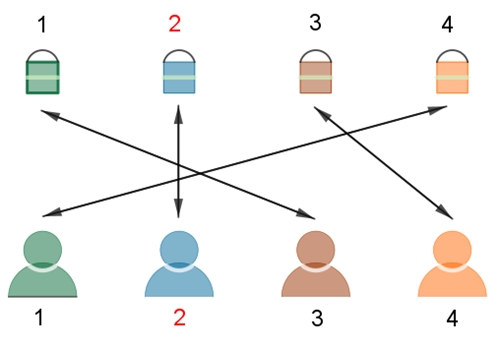
Beispiele einer zufälligen Verteilung, im rechten Fall erhält die 2. Person ihr eigenes Geschenk.

Bei der Lösung der Aufgabe geht es darum, dass n Personen (1, 2, 3, …,n) n Geschenke (1, 2, 3, …,n) zufällig umkehrbar eindeutig zugeordnet werden.
Dazu benötigt man den Begriff der Permutation:

Eine Permutation z.B. der Zahlen 1, 2, 3, . . . , n gibt eine Anordnungsmöglichkeit der n verschiedenen Zahlen an.

Die Anzahl aller möglichen Permutationen (Anordnungen) werden durch die Fakultät i.Z. ! dargestellt:

n! = 1⸱2⸱3⸱. . .⸱n

Veranschaulichung z.B. der Permutation 1 ⟶ 3, 2 ⟶ 1, 3 ⟶ 2

In Zweizeilenform: 

In Tupelschreibweise:  (3, 1, 2), in obiger linker Figur (3, 4, 2, 1), in rechter Figur (3, 2, 4, 1)

Der Fixpunkt einer Permutation ist dadurch gekennzeichnet, dass bei der Tupelschreibweise an der i-ten Stelle die Zahl i steht:

Beispiele in Tupelschreibweise, Fixpunkte sind rot dargestellt:

n=1: 1! = 1

(1), 0% fixpunktfrei

n=2: 2! = 2

(1, 2), (2, 1), 50% fixpunktfrei

n=3: 3! = 6

(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1):  33% fixpunktfrei

n=4: 4! = 24

(1 ,2, 3, 4), (1, 2, 4, 3), (1, 3, 2, 4), (1, 3, 4, 2), (1, 4, 2, 3), (1, 4, 3, 2),
(2, 1, 3, 4), (2, 1, 4, 3), (2 ,3, 1, 4), (2, 3, 4, 1), (2, 4, 1, 3), (2, 4, 3, 1),
(3, 1, 2, 4), (3, 1, 4, 2), (3, 2, 1, 4), (3, 2, 4, 1), (3, 4, 1, 2), (3, 4, 2, 1),
(4, 1, 2, 3), (4, 1, 3, 2), (4, 2, 1, 3), (4, 2, 3, 1), (4, 3, 1, 2), (4, 3, 2, 1):

9 von 24 sind fixpunktfrei, das sind 37,5%.

Allgemein gilt für die Anzahl der fixpunktfreien Permutationen in Abhängigkeit von n:

z.B: n=4:  ! 4 = 24⸱(1 – 1 + 1/2 – 1/6  + 1/24) = 9

Für die Wahrscheinlichkeit der fixpunktfreien (fixpfr)  Permutationen gilt dann in Abhängigkeit von n:

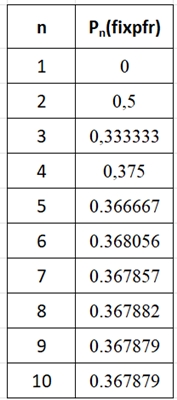
Tabelle für n ∊ {1, 2, 3, . . ., 10}

Grenzwert von P_n(fixpfr) für n gegen unendlich:

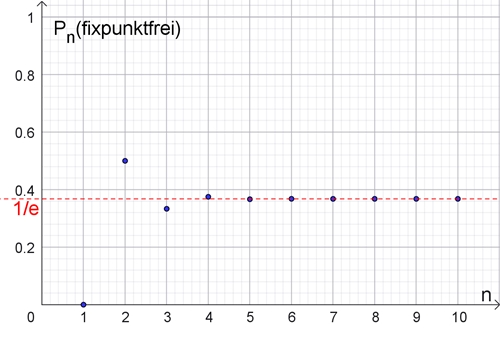
Es fällt auf, dass bereits bei n = 7 die Wahrscheinlichkeit für eine fixpunktfreie Permutation dem Grenzwert sehr nahe kommt.

NR: Taylor-Reihe der Exponentialfunktion

Für x = –1 folgt obiger Grenzwert.

Grafische Darstellung von P_n(fixpfr) in Abhängigkeit von n

Übertragen auf das Ausgangsproblem gilt dann:

Mit einer Wahrscheinlichkeit von etwa 36,8% erhält bei mehr als 5 Personen keine Person ihr eigenes Geschenk.

Umgekehrt gilt mit einer Wahrscheinlichkeit von ungefähr 1 – 0,368 = 63,2% (Gegenwahrscheinlichkeit), dass mindestens eine Person bei mehr als 5 Personen ihr eigenes Geschenk erhält.

Das Ergebnis ist verblüffend und zählt zu den Paradoxien der Wahrscheinlichkeit.

Zurück
Zurück zur Startseite