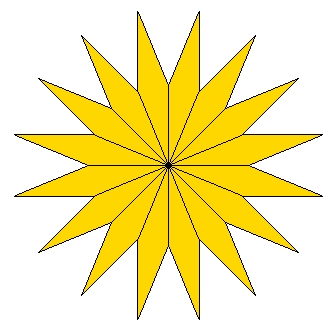
Sterne in regelmäßigen Vielecken, Sternformen 

Ein regelmäßiger Stern entsteht z.B., wenn man die Eckpunkte eines regelmäßigen Vielecks mit einem nicht benachbarten Eckpunkt so verbindet, dass alle Kanten gleich lang sind.

Die folgenden regelmäßigen Sterne besitzen die gleiche Anzahl von Symmetrieachsen wie die zugehörigen regelmäßigen Vielecke.

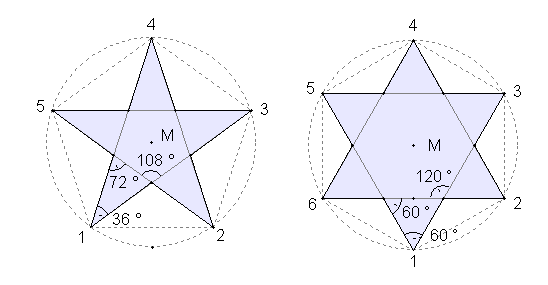
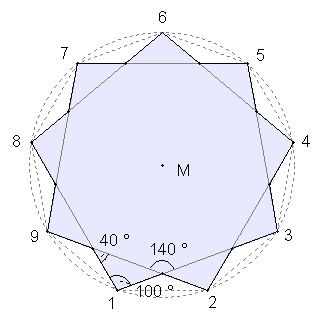
Werden die Ecken des n-Ecks durchnummeriert und nur die Eckpunkte verbunden deren Differenz die gleiche Differenz d>1 haben, so spricht man von einem {n/d}-Stern.

Sterne im regulären Fünf- und Sechseck mit unterschiedlichen Winkeln:

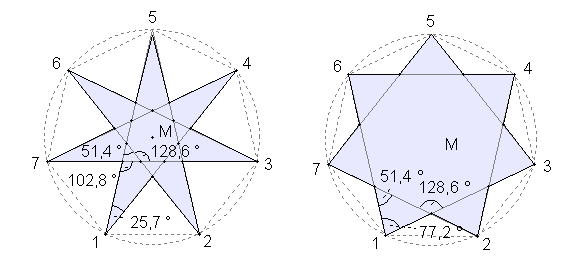
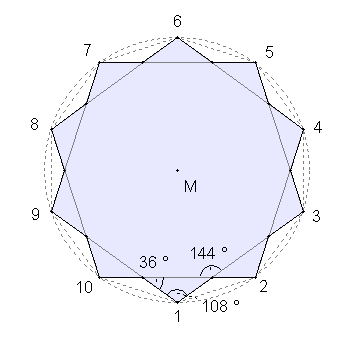
Zwei Sternformen im regulären Siebeneck mit unterschiedlichen Winkeln auf 1 Dezimale gerundet:

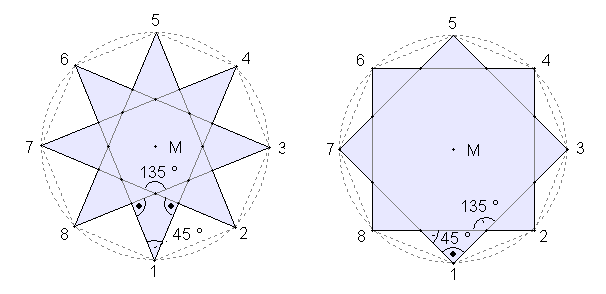
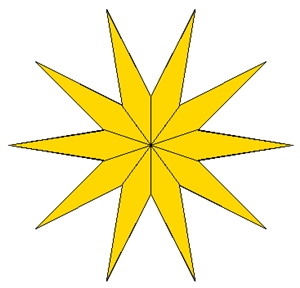
                    {7/3}-Stern                                   {7/2}-Stern

Zwei Sternformen im regulären Achteck mit unterschiedlichen Winkeln:

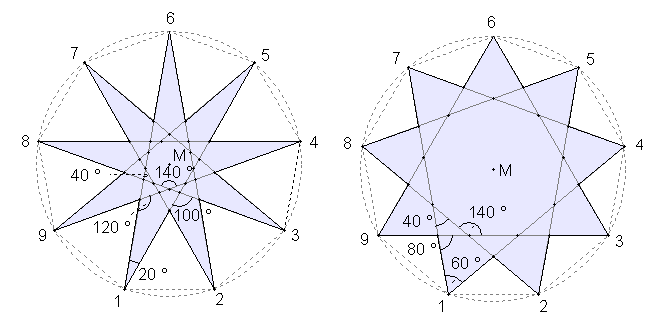
                    {8/3}-Stern                                   {8/2}-Stern

Drei Sternformen im regulären Neuneck mit unterschiedlichen Winkeln:

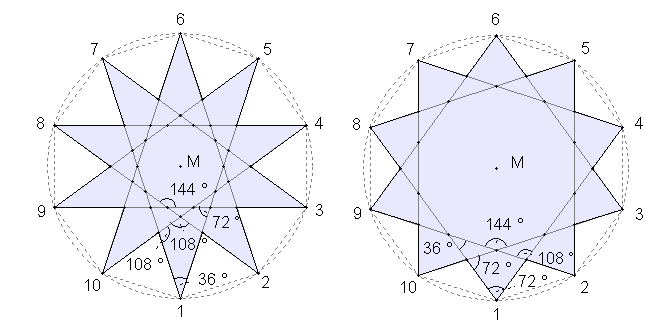
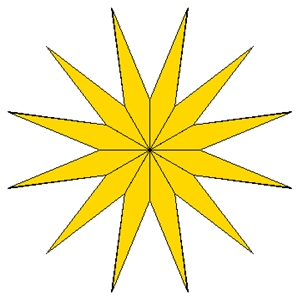
                {9/4}-Stern                                   {9/3}-Stern                                   {9/2}-Stern

Drei Sternformen im regulären Zehneck mit unterschiedlichen Winkeln:

                {10/4}-Stern                                 {10/3}-Stern                                 {10/2}-Stern

Je höher die Eckenzahl ist, umso mehr verschiedene Sternformen gibt es zu einem bestimmten n-Eck.

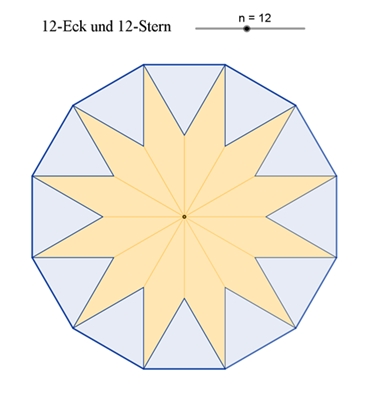
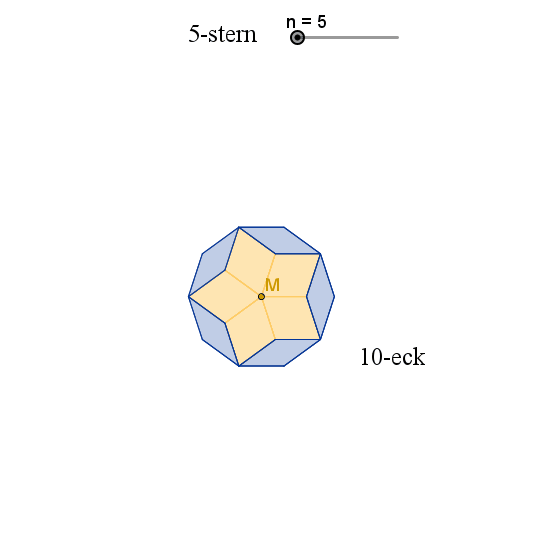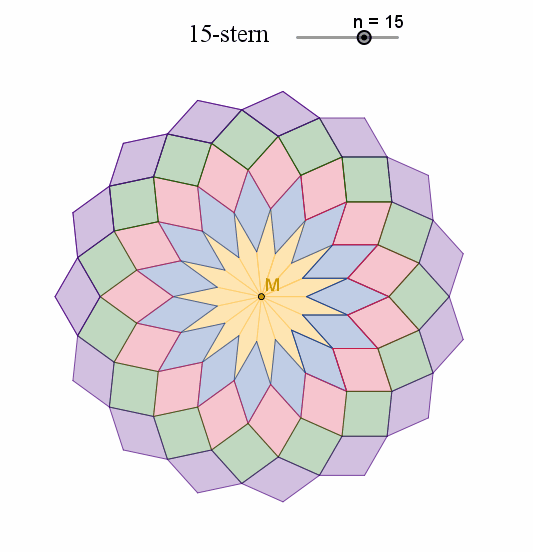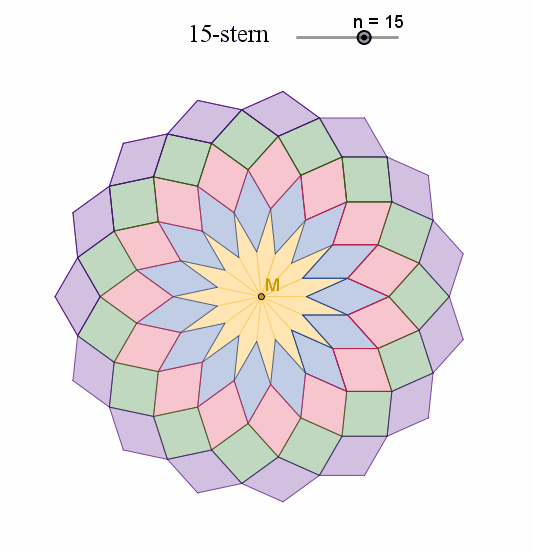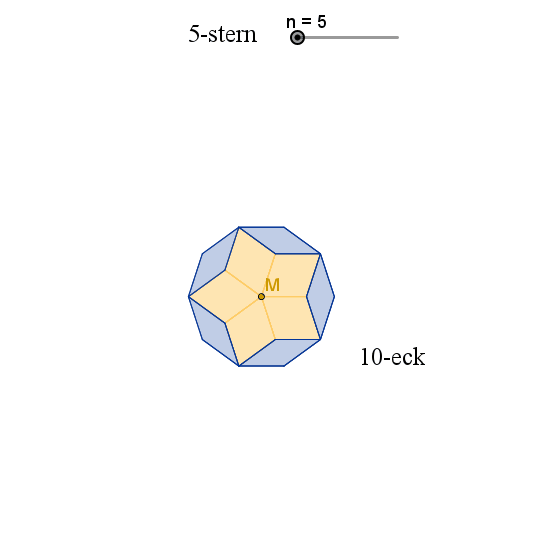
Sterne aus kongruenten Rauten

   Spitzer Winkel der Raute:
             360° : 5 = 72°                                  360° : 6 = 60°                               360° : 7 ≈ 41,43°                        360° : 8 =  45°

   Spitzer Winkel der Raute:
            360° : 9 = 40°                                 360° : 10 = 36°                               360° : 12 = 30°                           360° : 16 = 22,5°       

Die Ecken der Rauten-Sterne liegen auf regelmäßigen (regulären) Vielecken.

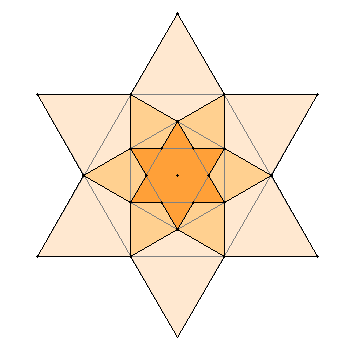
Ineinander geschachtelte Sterne am Beispiel des regelmäßigen Sechsecks:

Der Abbildungsfaktor der Ähnlichkeitsabbildung, die den jeweils nächstkleineren Stern erzeugt, ist .

Begründung mit Hilfe des Satzes von Pythagoras oder mit Hilfe der zentrischen Streckung mit Zentrum M.

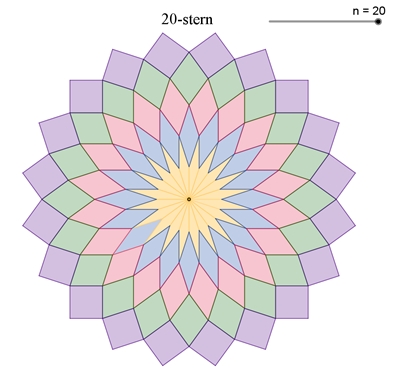
Vom 5- bis zum 20-Eck mit Rauten-Stern,  vom 5- bis zum 20-eckigen Rauten-Stern

                Sternenkränze mit 6- und 8-eckigen Rauten-Sternen,                    mit 8-10-12-eckigen Rauten-Sternen

Spitze Sternformen aus kongruenten Drachenvierecken, vom 5-Eck-Stern bis zum 12-Eck-Stern

Goldener Stern

Goldene Schnittzahl: (s. goldener Schnitt)

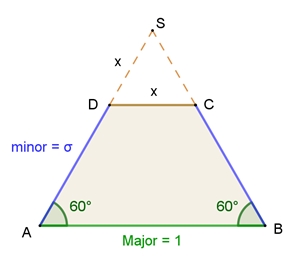
Trapez mit goldenem Schnitt

1 / x = (σ + x) / x     (Strahlensatz)

1 = σ + x

x = 1 – σ = σ²

Daraus folgt:

Wenn |AD| Major ist, ist |DC| minor.

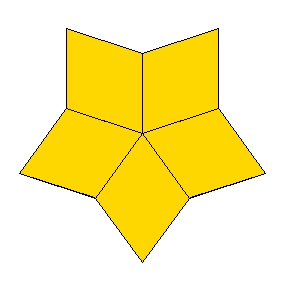
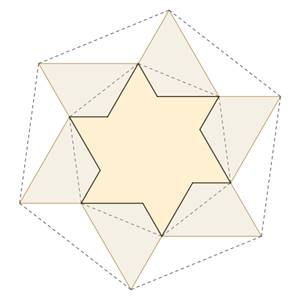
Wenn 6 solche Trapeze ringförmig angeordnet werden, entsteht ein „Goldener Stern“.

Die Sternspitzen bilden ein reguläres Sechseck.

                                                      Beliebte Sternformen variiert

                                                                            Fadensterne