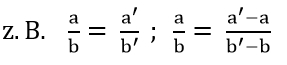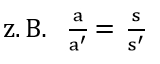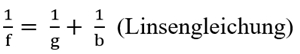Satz von Desargues und Strahlensatz

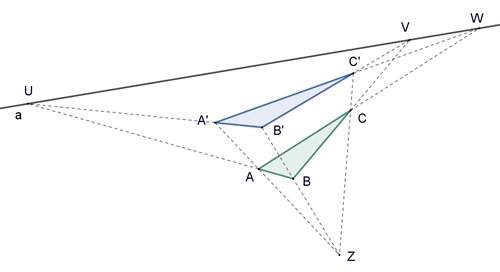
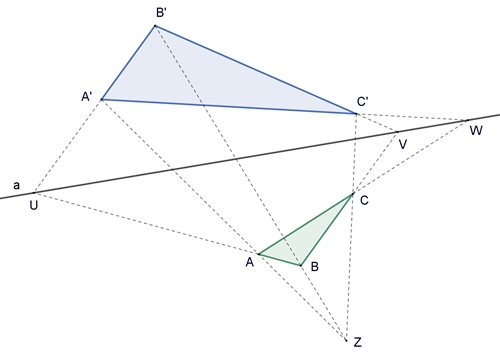
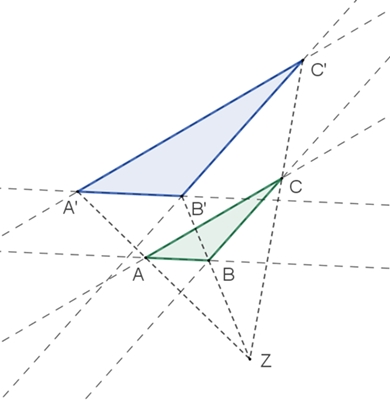
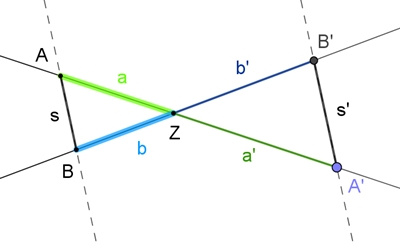
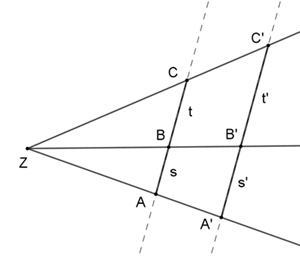
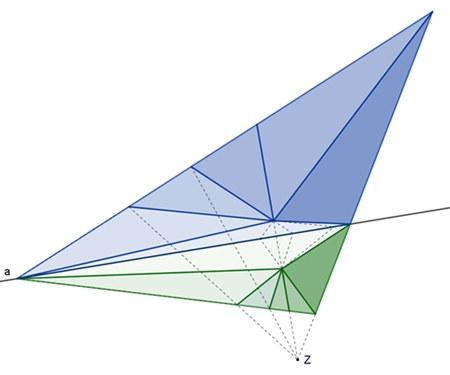
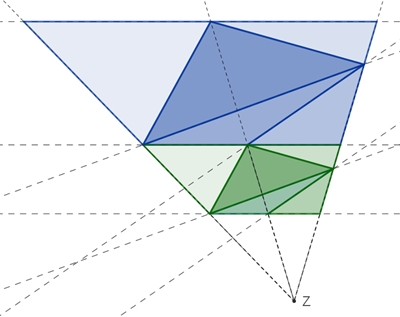
Satz von Desargues

Der Satz von Desargues, benannt nach dem französischen Mathematiker Gérard Desargues (1591 – 1661). Er gilt als Begründer der projektiven Geometrie.

Projektive Form des Satzes:

Wenn sich die Geraden durch die korrespondierenden Eckpunkte zweier in einer Ebene gelegenen Dreiecke in einem Punkt Z (Zentrum) schneiden, so liegen die Schnittpunkte der entsprechend verlängerten nichtparallelen Seiten auf einer Geraden (Achse a). Die Umkehrung des Satzes gilt auch.

Zentrische Streckung

Im Gegensatz zum Satz von Desargues gilt:  AB || A´B´,  BC || B´C´ und AC || A´C´

Dreieck ABC wird zentrisch gestreckt zu Dreieck A´B´C´ mit dem Zentrum Z und dem Faktor k = |ZA´| : |ZA|.

Die zentrische Streckung mit Streckungszentrum Z und Streckungsfaktor k > 0 ist eine Abbildung der Ebene auf sich, die jedem Punkt P seinen Bildpunkt P´ folgendermaßen zuordnet:
P´ liegt auf dem Strahl ZP, wobei gilt:  |ZP´| = k ٠ |ZP|  und  Z´ = Z.

Daraus lassen sich die Strahlensätze folgern.

Strahlensätze

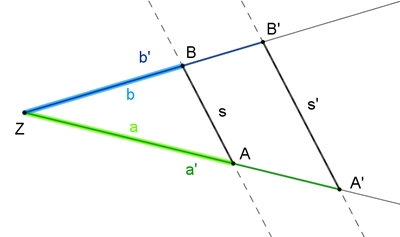
1. Strahlensatz

Werden zwei Geraden, die sich in einem Punkt Z schneiden von zwei Parallelen, die Z nicht enthalten, geschnitten, so verhalten sich je zwei Abschnitte auf der einen Geraden wie die entsprechenden Abschnitte auf der anderen Geraden.

2. Strahlensatz

Werden zwei Geraden, die sich in einem Punkt Z schneiden, von zwei Parallelen, die Z nicht enthalten, geschnitten, so verhalten sich die Abschnitte auf den Parallelen wie die von Z aus gehenden entsprechenden Abschnitte auf der einen oder anderen Geraden.

Umkehrung des 1. Strahlensatzes

Werden zwei Geraden, die sich in einem Punkt Z schneiden, von zwei Geraden, die Z nicht enthalten, geschnitten und sind die Verhältnisse der Längen entsprechender vom Anfangspunkt ausgehender Strahlenabschnitte gleich groß, so sind die beiden Geraden parallel.

Die Umkehrung des 2. Strahlensatzes gilt nicht!

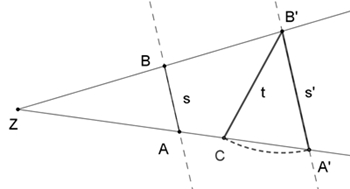
3. Strahlensatz

Werden drei Geraden, die sich in einem Punkt Z schneiden, von zwei parallelen Geraden, die Z nicht enthalten, geschnitten, so sind die Verhältnisse der Längen entsprechender paralleler Geradenabschnitte gleich groß. 

                                 s : t  =  s´ :  t´

Anwendungen der Strahlensätze

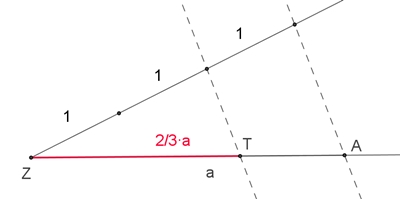
Teilung einer Strecke:

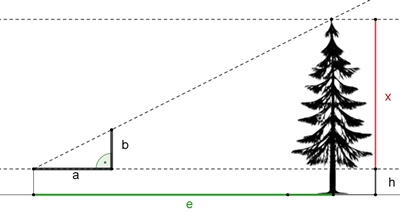
Bestimmung der Höhe einer Tanne:

x : e = b : a   Höhe der Tanne:  x + h = b/a٠e + h
 

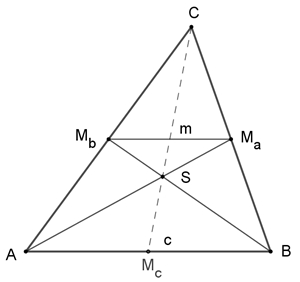
Schwerpunkt des Dreiecks:

M_bM_a || AB 

|AC| : |M_bC| = 2 : 1,  s : m = 2 : 1,  |AS| : |SM_a| = 2 : 1,  |BS| : |SM_b| = 2 : 1

Entsprechend:  |CS| : |SM_c| = 2 : 1

Der Schnittpunkt S der drei Seitenhalbierenden des Dreiecks ist der Schwerpunkt des Dreiecks. Er teilt die Seitenhalbierenden jeweils im Verhältnis 2 : 1.
 

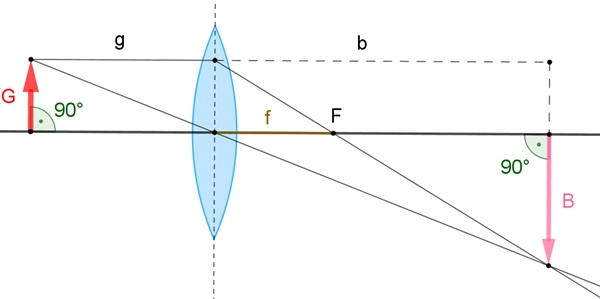
Abbildung durch eine Sammellinse, Linsengleichung

G : B  =  g  :  b   und  G :  B  =  f  :  (b-f)

Daraus folgt:   g  :  b  =  f  :  (b-f)

g٠(b-f)  =  bf  oder  bg – fg  = bf  oder  bg  =  bf  +  fg | : bgf

              Desargues-Dreiecke                                           Zentrisch gestreckte Dreiecke

Zurück
Zurück zur Startseite