Gruppe, zyklische Gruppe, Diedergruppe, symmetrische Gruppe und Translationsgruppe

Definition1:

Eine Gruppe (G, _° )  ist eine Menge G  und eine auf dieser Menge definierte Verknüpfung  „ _° “, die folgende Eigenschaften hat:

1)  (G, _° ) ist abgeschlossen, d.h. für alle a, b G gilt:  a _° b ist ebenfalls Element von G.

2)  (G, _° ) ist assoziativ, d.h. für alle a, b, c G gilt: a _° (b _° c) = (a _° b) _° c.

3)  In (G, _° ) existiert ein neutrales Element e, so dass für alle a  G gilt: e _° a = a _° e = a.

4)  Zu jedem Element a G existiert ein inverses Element a ^-1 G mit  a _° a ^-1 = a ^-1 _° a = e.

Ist die Gruppe auch kommutativ, gilt also für alle a, b G  a _° b = b _° a, so heißt die Gruppe abelsche Gruppe.

Eine nichtleere Teilmenge einer Gruppe (G, _° ), die bezüglich der Verknüpfung  „ _° “ selbst wieder eine Gruppe bildet, heißt Untergruppe U von G.  

Oft schreibt man statt "Gruppe (G, _° )"  "Gruppe G mit der Verknüpfung _{° "}, oder kurz nur "Gruppe G", falls die Verknüpfung festgelegt ist.

Definition2:

Die zyklische Gruppe C_n der Ordnung n besteht aus den Drehungen um das Vielfache von  eines regelmäßigen n-Ecks um seinen Mittelpunkt als Drehzentrum. Die Verknüpfung (Gruppenoperation) ist die Hintereinanderausführung von Drehungen. 

Die zyklische Gruppe C₃ = {i, d_1, d₂}

Bezeichnungen:

d₁ :  Drehung um 120° gegen den Uhrzeigersinn mit Drehzentrum M

d₂ :  Drehung um 240° gegen den Uhrzeigersinn mit Drehzentrum M

i = d₃ :  identische Abbildung = Drehung um 360° gegen den Uhrzeigersinn mit Drehzentrum M

Die Gruppenoperation _° ist die Hintereinanderausführung von Drehungen.

d₁ heißt erzeugendes Element der zyklischen Gruppe, wobei gilt:

d₂ = d_1° d₁ = d₁² ,    i =  d₃ = d_1° d_1° d₁  = d₁³ . 

Die Verknüpfung zweier Abbildungen erfolgt von links nach rechts.

Die Gruppentafel (Verknüpfungstafel):

1. Abbildung in der 1. Spalte, 2. Abbildung in der obersten Zeile.

Die zyklische Gruppe C₃ ist kommutativ. Die Gruppentafel ist symmetrisch bezüglich der Hauptdiagonale.
Die zyklische Gruppe C₃ kann nur von dem Element d₁ erzeugt werden: C₃ = { d_1, d₁²_, d₁³ }, wobei gilt: d₁²  = d_1° d₁, d₁³  = d_1° d_1° d₁  = i. 

Definition3:

Die Diedergruppe D_n der Ordnung 2n (Anzahl der Elemente) besteht für n ≥ 3 aus den Drehungen um das Vielfache von   eines regelmäßigen n-Ecks um seinen Mittelpunkt als Drehzentrum und den n verschiedenen Achsenspiegelungen. Die Gruppenoperation ist die Hintereinanderausführung von Drehungen und Spiegelungen.

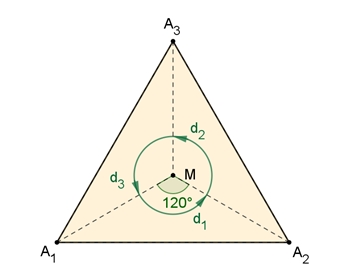
Die Diedergruppe D₃ = {i, s_1, s_2, s_3, d_1, d₂}

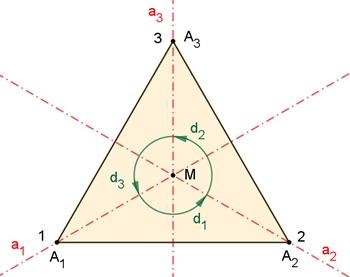   Bezeichnungen:

s₁    :   Spiegelung an der Achse a₁

s₂    :   Spiegelung an der Achse a₂

s₃    :   Spiegelung an der Achse a₃

d₁ :  Drehung um 120° gegen den Uhrzeigersinn mit Drehzentrum M

d₂ :  Drehung um 240° gegen den Uhrzeigersinn mit Drehzentrum M

i = d₃ :  identische Abbildung = Drehung um 360° gegen den Uhrzeigersinn mit Drehzentrum M.

Die Gruppenoperation _° ist die Hintereinanderausführung von Spiegelungen und Drehungen.

Die Gruppentafel 

1. Abbildung linke Spalte, 2. Abbildung 1. Zeile

o	i	d1	d2	s1	s2	s3
i	i	d1	d2	s1	s2	s3
d1	d1	d2	i	s2	s3	s1
d2	d2	i	d1	s3	s1	s2
s1	s1	s3	s2	i	d2	d1
s2	s2	s1	s3	d1	i	d2
s3	s3	s2	s1	d2	d1	i

  

Die Diedergruppe D₃ ist nicht kommutativ, da die Gruppentafel keine Symmetrie zur Hauptdiagonalen besitzt.  

Die zyklische Gruppe C₃ (hellgrün) ist eine Untergruppe der Diedergruppe D₃.

Definition4:

Die symmetrische Gruppe S_n ist die Gruppe, die aus allen Permutationen (Vertauschungen) einer n-elementigen Menge besteht. Die Gruppenoperation ist die Verkettung (Hintereinanderausführung) der Permutationen; das neutrale Element ist die Permutation, die alle Elemente invariant lässt.

Die symmetrische Gruppe S_n ist endlich und besitzt die Ordnung n!; für n > 2 ist sie nicht kommutativ.
 

Die symmetrische Gruppe S₃

Die symmetrische Gruppe S₃ besteht aus 6 Elementen, den Permutationen einer dreielementigen Menge, z.B. der Menge {1, 2, 3}.

a) S₃ in Matrixschreibweise:

    In der 2. Zeile stehen jeweils die zugeordneten Zahlen.

b) S₃ in Tupelschreibweise:

     { (1,2,3), (2,3,1), (3,1,2), (1,3,2), (3,2,1), (2,1,3) }, kurz: { 123, 231, 312, 132, 321, 213 }

    Sie enthält nur noch die 2. Zeile der Matrixdarstellung.

c) S₃ in Zyklenschreibweise:

    { (1) bzw.( ), (123), (132), (23), (13), (12) }

Die Gruppentafel in Tupelschreibweise:

		i	d1	d2	s1	s2	s3
	o	123	231	312	132	321	213
i	123	123	231	312	132	321	213
d1	231	231	312	123	321	213	132
d2	312	312	123	231	213	132	321
s1	132	132	213	321	123	312	231
s2	321	321	132	213	231	123	312
s3	213	213	321	132	312	231	123

Ein Vergleich der Verknüpfungstafeln von S₃ und D₃  liefert die gleiche Gruppenstruktur. Man sagt, dass die Symmetriegruppe S₃ isomorph zur Diedergruppe D₃ ist. Isomorphie (Isomorphismus) bedeutet dabei eine umkehrbar eindeutige Abbildung zwischen zwei mathematischen Strukturen.

Wenn man die Eckpunkte A₁, A₂ und A₃ des obigen gleichseitigen Dreiecks durch die Zahlen 1, 2 und 3 ersetzt, wird der Zusammenhang deutlich:

Die Permutationen (123), (132), (23), (13), (12) bzw. 231, 312, 132, 321, 213 entsprechen den Drehungen d₁, d₂ und den Spiegelungen s₁, s₂, s₃.  

Die beiden zugehörigen Gruppentafeln zeigen die gleiche Struktur.

Verknüpfung zweier Abbildungen in Matrixschreibweise:

s₁ o d₂ = s₂

Untergruppen:

Zyklische Gruppe C₃ = { 123, 231, 312 } (hellgrün)

Symmetrische Gruppen: S₂ = { 123, 132}, S₂ = { (123, 321) }, S₂ = { 123, 213 }

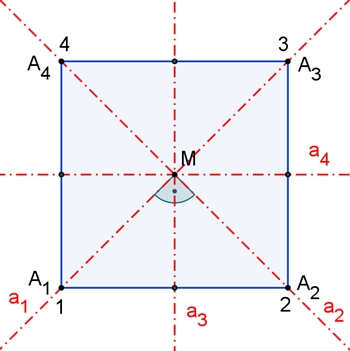
Die Diedergruppe D₄ = { i, d₁, d₂, d_3, s_1, s_2, s_3, s₄ }

Bezeichnungen:

d_n  =   Drehung um 90°٠n  gegen den Uhrzeigersinn mit Drehzentrum M,

i = d₄ =  identische Abbildung = Drehung um 360° gegen den Uhrzeigersinn mit Drehzentrum M,

s_n  =   Spiegelung an der Achse a_n , 

n  { 1, 2, 3, 4 }.

Die Gruppenoperation _° ist die Hintereinanderausführung von Spiegelungen und Drehungen.

Die Verknüpfung zweier Abbildungen erfolgt von links nach rechts.

Die Gruppentafel 

1. Abbildung linke Spalte, 2. Abbildung 1. Zeile

∘	i	d1	d2	d3	s1	s2	s3	s4
i	i	d1	d2	d3	s1	s2	s3	s4
d1	d1	d2	d3	i	s4	s3	s1	s2
d2	d2	d3	i	d1	s2	s1	s4	s3
d3	d3	i	d1	d2	s3	s4	s2	s1
s1	s1	s3	s2	s4	i	d2	d1	d3
s2	s2	s4	s1	s3	d2	i	d3	d1
s3	s3	s2	s4	s1	d3	d1	i	d2
s4	s4	s1	s3	s2	d1	d2	d3	i

Die Diedergruppe D₄ ist nicht kommutativ, da die Gruppentafel keine Symmetrie zur Hauptdiagonalen besitzt.  

Die zyklische Gruppe C₄ (hellgrün) ist eine kommutative Untergruppe der Diedergruppe D₄.

Die zyklische Gruppe C₄ kann nur mit dem Element d = d₁ erzeugt werden, wobei gilt:

C₄ = { d, d², d³, d⁴ = i }  mit d² = d∘d = d₂, d³ = d∘d∘d = d₃, d⁴ = d∘d∘d∘d = i.

Die Diedergruppe D₄ kann von den beiden Elementen  d = d₁ und  s₁ erzeugt werden, wobei gilt:  d _∘ s₁ = s₄ , d²∘ s₁ = s₂ , d³∘ s₁ = s₃.

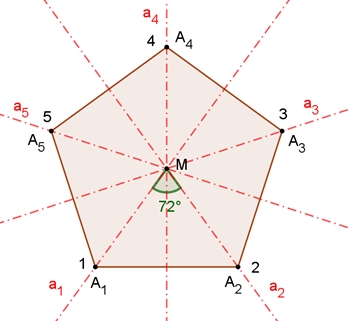
Die Diedergruppe D₅ = { i, d₁, d₂, d_3, d₄, s_1, s_2, s_3, s_4, s₅ }

Bezeichnungen:

d_n  =   Drehung um 72°٠n  gegen den Uhrzeigersinn mit Drehzentrum M ,

i = d₅ =  identische Abbildung = Drehung um 360° gegen den Uhrzeigersinn mit Drehzentrum M,

s_n  =   Spiegelung an der Achse a_n , 

n  { 1, 2, 3, 4, 5 }.

Die Gruppenoperation _° ist die Hintereinanderausführung von Spiegelungen und Drehungen. Die Verknüpfung zweier Abbildungen erfolgt von links nach rechts.

Die Gruppentafel 

1. Abbildung linke Spalte, 2. Abbildung 1. Zeile

∘	i	d1	d2	d3	d4	s1	s2	s3	s4	s5
i	i	d1	d2	d3	d4	s1	s2	s3	s4	s5
d1	d1	d2	d3	d4	i	s3	s4	s5	s1	s2
d2	d2	d3	d4	i	d1	s5	s1	s2	s3	s4
d3	d3	d4	i	d1	d2	s2	s3	s4	s5	s1
d4	d4	i	d1	d2	d3	s4	s5	s1	s2	s3
s1	s1	s4	s2	s5	s3	i	d2	d4	d1	d3
s2	s2	s5	s3	s1	s4	d3	i	d2	d4	d1
s3	s3	s1	s4	s2	s5	d1	d3	i	d2	d4
s4	s4	s2	s5	s3	s1	d4	d1	d3	i	d2
s5	s5	s3	s1	s4	s2	d2	d4	d1	d3	i

Die Diedergruppe D₅ ist nicht kommutativ, da die Gruppentafel keine Symmetrie zur Hauptdiagonalen besitzt.  

Die zyklische Gruppe C₅ (hellgrün) ist eine Untergruppe der Diedergruppe D₅.

Die zyklische Gruppe C₅ kann nur mit dem Element d = d₁ erzeugt werden, wobei gilt:

C₅ = { d, d², d³, d⁴, d⁵ = i }  mit d² = d _° d = d₂, usw.

Die Diedergruppe D₅ kann von den beiden Elementen  d = d₁ und  s₁ erzeugt werden, wobei gilt: d _° s₁ = s₃ , d²_° s₁ = s₅ , d³_° s₁ = s₂ , d⁴_° s₁ = s₄.

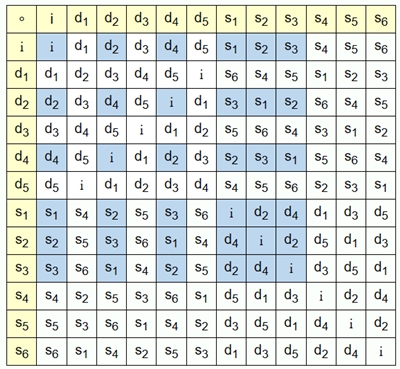
Die Diedergruppe D₆ = { i, d₁, d₂, d_3, d₄, d₅, s_1, s_2, s_3, s_4, s_5, s₆ }

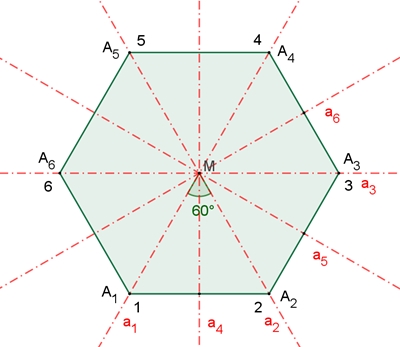
Bezeichnungen:

d_n  =   Drehung um 60°٠n  gegen den Uhrzeigersinn mit Drehzentrum M ,

i = d₆ =  identische Abbildung = Drehung um 360° gegen den Uhrzeigersinn mit Drehzentrum M,

s_n  =   Spiegelung an der Achse a_n, 

n { 1, 2, 3, 4, 5, 6 }.

Die Gruppenoperation _° ist die Hintereinanderausführung von Spiegelungen und Drehungen. Die Verknüpfung zweier Abbildungen erfolgt von links nach rechts.

Die Gruppentafel 

1. Abbildung linke Spalte, 2. Abbildung 1. Zeile

∘

i

d1

d2

d3

d4

d5

s1

s2

s3

s4

s5

s6

i

i

d1

d2

d3

d4

d5

s1

s2

s3

s4

s5

s6

d1

d1

d2

d3

d4

d5

i

s6

s4

s5

s1

s2

s3

d2

d2

d3

d4

d5

i

d1

s3

s1

s2

s6

s4

s5

d3

d3

d4

d5

i

d1

d2

s5

s6

s4

s3

s1

s2

d4

d4

d5

i

d1

d2

d3

s2

s3

s1

s5

s6

s4

d5

d5

i

d1

d2

d3

d4

s4

s5

s6

s2

s3

s1

s1

s1

s4

s2

s5

s3

s6

i

d2

d4

d1

d3

d5

s2

s2

s5

s3

s6

s1

s4

d4

i

d2

d5

d1

d3

s3

s3

s6

s1

s4

s2

s5

d2

d4

i

d3

d5

d1

s4

s4

s2

s5

s3

s6

s1

d5

d1

d3

i

d2

d4

s5

s5

s3

s6

s1

s4

s2

d3

d5

d1

d4

i

d2

s6

s6

s1

s4

s2

s5

s3

d1

d3

d5

d2

d4

i

Die Diedergruppe D₆ ist nicht kommutativ. 

Die zyklische Gruppe C₆ (hellgrün) ist eine Untergruppe der Diedergruppe D₆.

Die zyklische Gruppe C₆ kann nur mit dem Element d = d₁ erzeugt werden, wobei gilt:

C₆ = { d, d², d³, d⁴, d⁵, d⁶ = i }  mit d² = d _° d = d₂, usw.

Die Diedergruppe D₆ kann von den beiden Elementen  d = d₁ und  s₁ erzeugt werden, wobei gilt:  d _° s₁ = s₆ , d² _° s₁ = s₃ , d³ _° s₁ = s₅ , d⁴ _° s₁ = s₂, d⁵ _° s₁ = s₄.

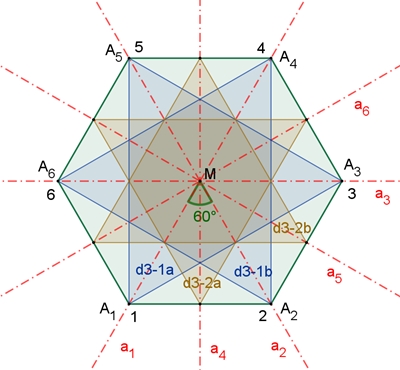
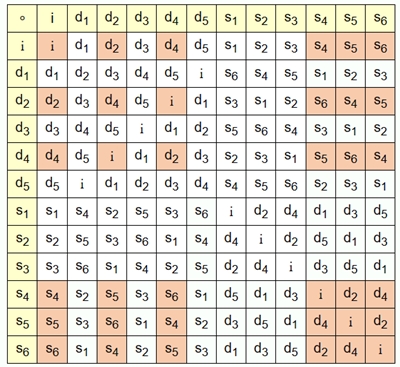
Die Diedergruppen D_3-1a, D_3-1b (blau) und D_3-2a, D_3-2b (braun) als Untergruppen der Diedergruppe D₆.

Die Gruppentafeln mit den Untergruppen

                D_3-1 = { i, d₂, d₄, s₁, s₂, s₃ }                                          D_3-2 = { i, d₂, d₄, s₄, s₅, s₆ }

Die Diedergruppe D₂ = { i, d, s_1, s₂ }

Veranschaulichung durch Rechteck oder Raute mit a ≠ b.

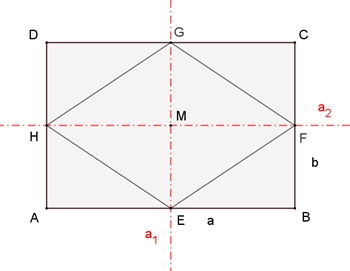
Bezeichnungen:

d  =   Drehung um 180°  gegen den Uhrzeigersinn mit Drehzentrum M,

i = d∘d =  identische Abbildung = Drehung um 360° gegen den Uhrzeigersinn mit Drehzentrum M,

s_n  =   Spiegelung an der Achse a_n , n { 1, 2 }.

Die Gruppentafel 

1. Abbildung linke Spalte, 2. Abbildung 1. Zeile

∘	i	d	s1	s2
i	i	d	s1	s2
d	d	i	s2	s1
s1	s1	s2	i	d
s2	s2	s1	d	i

Die Diedergruppe D₂ ist kommutativ, da die Gruppentafel eine Symmetrie zur Hauptdiagonalen besitzt.  

Die zyklische Gruppe C₂ = { i, d } (hellgrün) ist eine kommutative Untergruppe der Diedergruppe D₂.

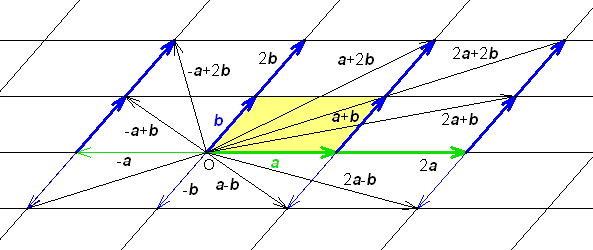
Definition5:

Die Linearkombination   x = m a + n b  der Verschiebungsvektoren a und b  mit ganzzahligen Parametern  m und n, bezogen auf einen beliebigen Knotenpunkt als Zentrum O, bildet die diskrete Translationsgruppe T eines ebenen Gitters.