Vierecke

Bezeichnungen beim Viereck

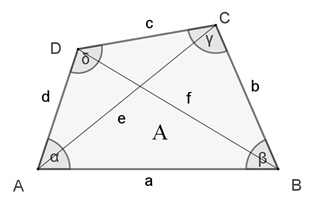
Viereck mit den Seiten a, b, c, d,
den Winkeln α, β, γ, δ,
den Diagonalen e, f
und dem Flächeninhalt A.

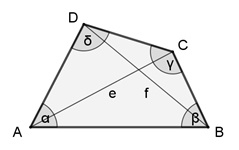
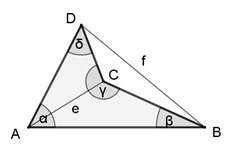
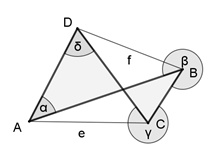
        konvexes Viereck                           konkaves Viereck                    überschlagenes Viereck

Beim konvexen Viereck liegen beide Diagonalen innerhalb des Vierecks.
Beim konkaven Viereck liegt eine Diagonale innerhalb und die andere Diagonale außerhalb des Vierecks.
Beim überschlagenen Viereck liegen beide Diagonalen außerhalb des Vierecks.

Im konvexen und konkaven Viereck gilt:

Die Summe der Innenwinkel ist gleich 360°:  α + β + γ + δ = 360°

Im überschlagenen Viereck gilt bei gleicher Winkelorientierung:  α + β + γ + δ = 720°

Vom speziellen zum allgemeinen komplexen Viereck

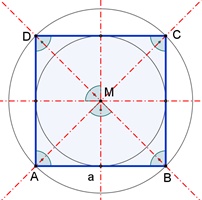
Das Quadrat   

Eigenschaften des Quadrats:

Alle Seiten sind gleich lang und gegenüberliegende Seiten sind parallel.

Die Innenwinkel sind alle gleich 90°.

 Die Diagonalen sind gleich lang, halbieren sich gegenseitig und schneiden sich im rechten Winkel.

Es besitzt 4 Symmetrieachsen und ist 4-fach rotationssymmetrisch um M mit den Drehwinkeln 90°, 180°, 270° und 360°.

Es besitzt einen Umkreis und einen Inkreis.

Flächeninhalt A = a²

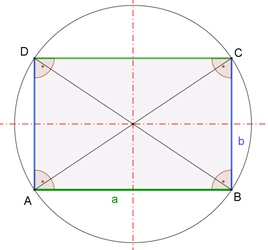
Das Rechteck

      Eigenschaften des Rechtecks:

Gegenüberliegende Seiten sind gleich lang und parallel.

Die Innenwinkel sind alle gleich 90°.

Die Diagonalen sind gleich lang und halbieren sich gegenseitig. Es besitzt einen Umkreis.

Es besitzt 2 Symmetrieachsen und ist 2-fach rotationssymmetrisch um M mit den Drehwinkeln 180° und 360°.

Flächeninhalt A = a٠b

Die Raute 

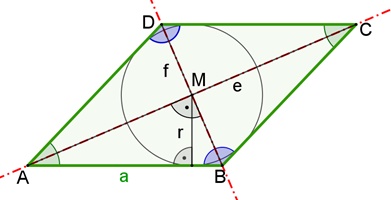
  Eigenschaften der Raute:

Alle Seiten sind gleich lang und gegenüberliegende Seiten sind parallel.

Zwei gegenüberliegende Winkel sind gleich groß.

Die Diagonalen e und f schneiden sich im rechten Winkel und halbieren sich gegenseitig. Die Dreiecke ABM, BCM, CMD und AMD sind rechtwinklig und kongruent.

Sie besitzt 2 Symmetrieachsen und ist 2-fach rotationssymmetrisch um M mit den Drehwinkeln 180° und 360°.

Sie besitzt einen Inkreis.

Flächeninhalt A = ½ e٠f

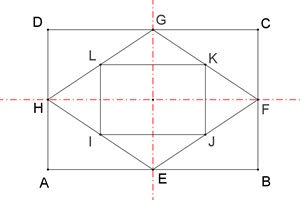
Zusammenhang zwischen Rechteck und Raute

Die Verbindungsstrecken der Seitenmitten des Rechtecks ABCD liefert die Raute EFGH.
Die Verbindungsstrecken der Seitenmitten der Raute EFGH liefert das Rechteck IJKL

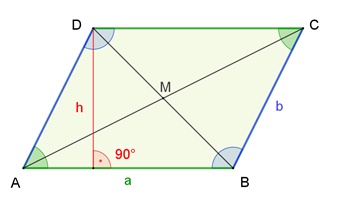
Das Parallelogramm

Eigenschaften des Parallelogramms:

Gegenüberliegende Seiten sind gleich lang und parallel.

Zwei gegenüberliegende Winkel sind gleich groß.

Es ist 2-fach rotationssymmetrisch um M mit den Drehwinkeln 180° und 360°.

Flächeninhalt A = a٠h

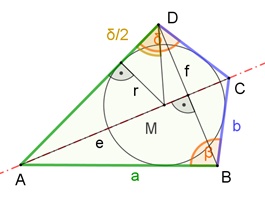
Das Drachenviereck

Eigenschaften des Drachenvierecks:

Die Strecken a und b und die Strecken c und d sind gleich lang (△ABD und △BCD sind gleichschenklig)

Die Winkel β und δ sind gleich groß.

Die Diagonalen stehen senkrecht aufeinander.

Es besitzt einen Inkreis.

Flächeninhalt A = ½ e٠f

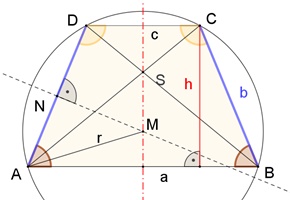
Das gleichschenklige Trapez

Eigenschaften des gleichschenkligen Trapezes:

Die Seiten b und d sind gleich lang.

Die gegenüberliegenden Seiten a und c sind parallel.

Die Basiswinkel α und β und die Winkel γ und δ sind gleich groß.
Die Diagonalen sind gleich lang.

Es besitzt eine Symmetrieachse und einen Umkreis.

Flächeninalt A = ½ (a+c)٠h

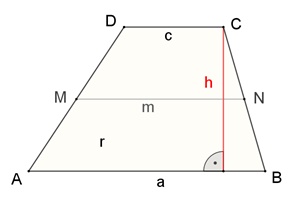
Das Trapez

Eigenschaften desTrapezes:

Die gegenüberliegenden Seiten a und c sind parallel.
Mittellinie m = ½ (a+c)

Flächeninalt A = ½ (a+c)٠h

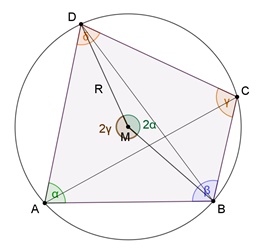
Das Sehnenviereck

Eigenschaften des Sehnenvierecks:

Die Winkelsumme gegenüberliegender Winkel beträgt 180°, 
α + γ = 180° und β + δ = 180°.

Mittelpunktswinkel ∡BMD = 2α und ∡DMB = 2γ.
Entsprechend ∡AMC = 2δ und ∡CMA = 2β.

Begründungen: Kreis- und Umfangswinkelsatz, mit Umfangswinkel über [BD] und [AC]).

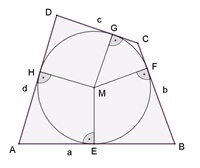
Das Tangentenviereck

Eigenschaften des Tangentenvierecks:

a + c = b + d (Begründung: Tangentenviereck)

Die Vierecke AEMH, BFME, CGMF und DHMG sind Drachenvierecke mit zwei gegenüberliegenden rechten Winkeln.

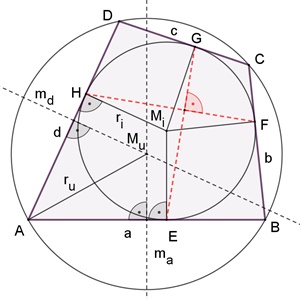
Das Sehnen-Tangenenviereck

Eigenschaften des Sehnen-Tangenenviereck

Die Berührungssehnen zweier gegenüberliegender Berührungspunkten stehen senkrecht aufeinander, HF ⏊ EG.
(Begründung: Sehnen-Tangentenviereck)

Der Inkreismittelpunkt M_i ist der Schnittpunkt der Winkelhalbierenden der Innenwinkel.

Der Umkreismittelpunkt M_u ist der Schnittpunkt der Mittelsenkrechten der Seiten des Vierecks.

Das Quadrat ist ein spezielles Sehnen-Tangenenviereck.

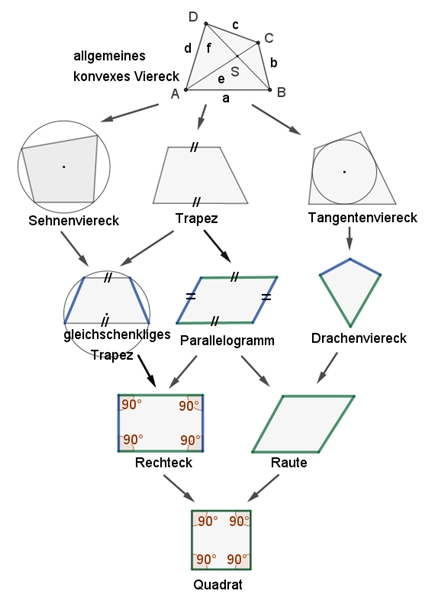
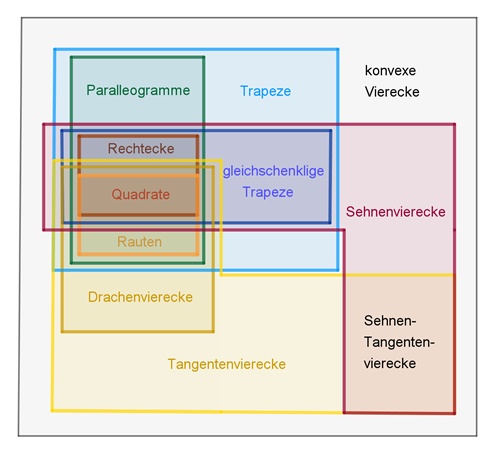
Übersicht über die konvexen Viereckstypen

Das nachfolgende Viereck besitzt alle Eigenschaften des vorhergehenden Vierecks.

Die Menge der konvexen Vierecke

Veranschaulichung der logischen Beziehungen zwischen den verschiedenen Vierecksarten in einem Mengendiagramm.

Teilmengen:

Quadrate ⊂ Rechtecke ⊂ Parallelogramme ⊂ Trapeze ⊂ konvexe Vierecke ⊂ Vierecke

⊂ bedeutet: „ist echte Teilmenge von“

Schnittmengen:

Die Menge der Quadrate ist die Schnittmenge aus der Menge der Rechtecke und der Menge der Rauten, i.Z:
{Quadrate} = {Rechtecke} ∩ {Rauten} (lies: „geschnitten mit“)

Entsprechend gilt:

{Quadrate} = {Drachenvierecke} ∩ {gleichschenklige Trapeze}
{Rechtecke} = {Sehnenvierecke} ∩ {Parallelogramme}
{Rauten} = {Drachenvierecke} ∩ { Parallelogramme }
{Gleichschenklige Trapeze} = {Sehnenvierecke} ∩ {Trapeze}

Verschachtelte Vierecke

Sternenkränze mit 6-, 8,- ,10- und 12-eckigen Sternen aus Rauten