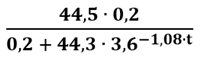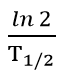Anwendungsbeispiele für Wachstum und Zerfall, für die Exponentialfunktion und die logistische Funktion

Verzinsung

Ein Kapital K(0) =1000 € wird zu 2,5% verzinst.

Berechnung des Guthabens (Kapitals) K(t) nach t = 1, 2, 3, . . . Jahren:

K(1) = K(0)٠1,025

K(2) = K(0)٠1,025٠1,025  = K(0)٠1,0252

K(3) = K(0)٠1,0253

. . .

K(t) = K(0) × 1,025 t mit K(0) = 1000 €

Nach z.B. t = 10 Jahren ergibt sich:

K(10) = 1000 €٠1,02510  = 1280,08 €

Verdopplung des Kapitals:

2٠K(0) = K(0)٠1,025 t  ⇒  t = ln 2 / ln 1,025  ≈  28

Eine Verdopplung des Kapitals ergibt sich nach etwa 28 Jahren.

(ln = natürlicher Logarithmus = Logarithmus zur Basis e ≈ 2,71828)

 

Bakterienwachstum

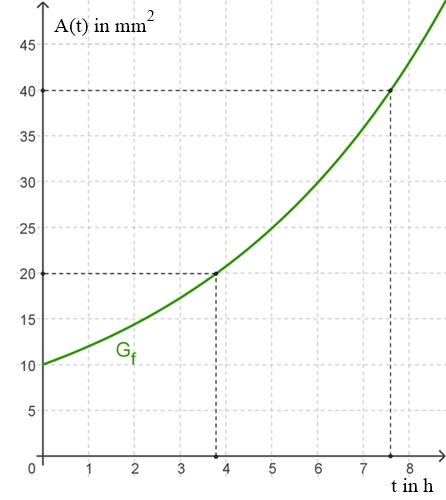
Ein Biologe stellt bei der Beobachtung einer Bakterienkultur fest, dass sich die von den Bakterien bedeckte Fläche A(t) in der Petrischale jede Stunde um 20% vergrößert, d.h. die 1,2-fache Fläche einnimmt.
Berechnung der Fläche nach t = 1, 2, 3, ..., n Stunden (h), wenn sie zu Beginn der Beobachtung 10 mm2 groß war:

A(1) = A(0)٠1,2   mit  A(0) = 10 mm2

A(2) = A(0)٠1,2 ٠1,2  =  A(0)٠1,2 2 

A(3) = A(0)٠1,2 3 

. . .

A(t) = A(0)٠1,2 t  mit  A(0) = 10 mm2

Graphische Darstellung von A(t) in Abhängigkeit von t

Verdopplung der Fläche: A(t) = 2٠A(0) 

 ⇒ 1,2 t  = 2  ⬄  ln 1,2 t  = ln 2  ⬄ t٠ln 1,2 = ln 2  ⇒  t ≈ 3,8

Nach jeweils 3,8 Stunden verdoppelt sich die mit Bakterien bedeckte Fläche.

(ln = natürlicher Logarithmus = Logarithmus zur Basis e ≈ 2,71828)

Das Wachstum ist jedoch durch die Größe der Petrischale begrenzt!

 

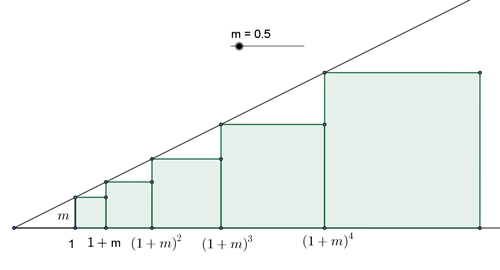
Exponentielle Quadrat-Folge

Die obere Gerade habe die Steigung m. Der linke untere Eckpunkt der Quadrate habe den Wert ak, a1 = 1, k ∊ ℕ.

Quadrat-Folge-1

Für die Steigung m gilt:  m = (ak+1 – ak)/ak

Daraus ergibt sich die Rekursion:  ak+1 = ak (m +1) 

Die Seitenlängen der Quadrate bilden dann eine geometrische Folge mit dem Quotienten ak+1/ak = q = m + 1.

NR:
((1+m)2– (1+m))/(1+m) = 1+m – 1 = m
((1+m)3-(1+m)2)/(1+m)2 = 1+m – 1 = m
usw.

Entsprechend bilden die Quadratflächen eine geometrische Folge mit dem Quotienten (m + 1)2 und dem Anfangsglied m2.

Für die Summe der Quadratflächen A als geometrische Reihe gilt dann

A = m2 + m2(1+m)2 + m2(1+m)4 + … + m2(1+m)2n = m2 ((1+m)2n – 1)/( (1+m)2 – 1)

A = m ((m+1)2n – 1)/(m+2)

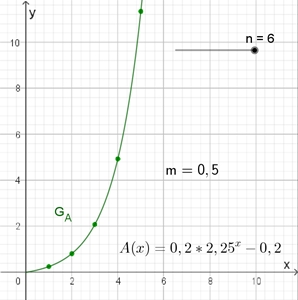
Für m = 0,5 folgt: A = (2,25n – 1)/5

Quadrat-Folge-2

 

  

Der Graf der Funktion A in Abhängigkeit von n stellt Punkte dar, die auf einer Exponentialfunktion liegen.

 

 

 

 

 

  

Bevölkerungswachstum

Die Weltbevölkerung ist in der Vergangenheit angenähert exponentiell gewachsen.

Gleichung der Exponentalfunktion zur Näherung des Bevölkerungswachstums zwischen 1950 und 2020:

f(x) = f(0)٠1,0153 10٠t   mit  f(0) = 2,8٠106 Menschen im Jahr 1950 (für Näherung 2,8 statt 2,54)

1 Zeiteinheit für t entspricht 10 Jahre. Die Basis 1,0153 = 1 + 1,53%

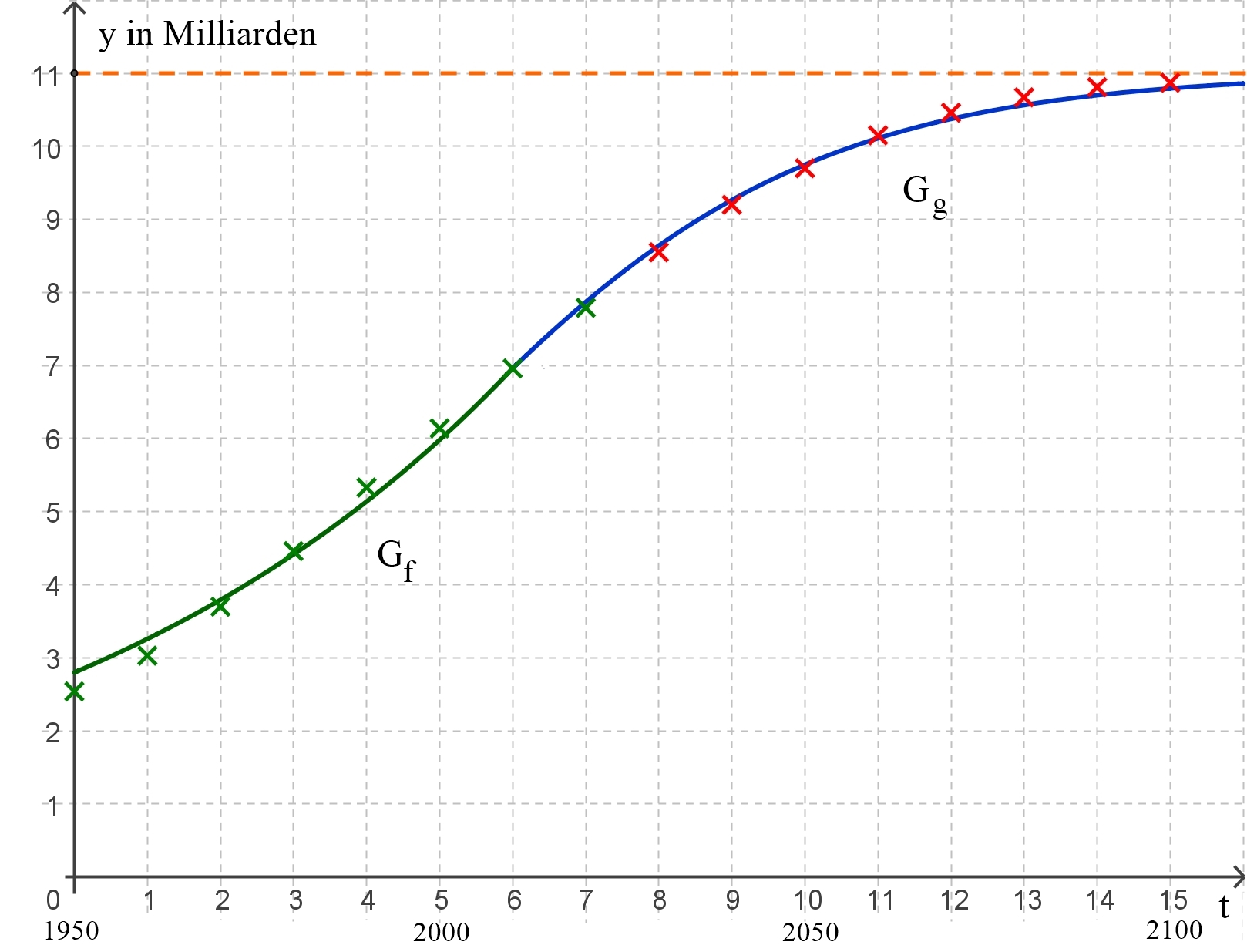
1,53% ist das mittleres Wachstum zwischen 1950 und 2000.

Statistikwerte sind als grüne Punkte dargestellt,

prognostizierte Werte als rote Punkte, Grenzwert 11 Milliarden Menschen, Quelle: https://de.statista.com

Gleichung der logistischen Funktion zur Darstellung der möglichen weiteren Bevölkerungsentwicklung ab 2020:

g(x) =

Startwert g(6) = 6,96 bei t = 6 (im Jahr 2010)

Graphische Darstellung Gf (grün) und Gg (blau) des Bevölkerungswachstums der Welt:

 

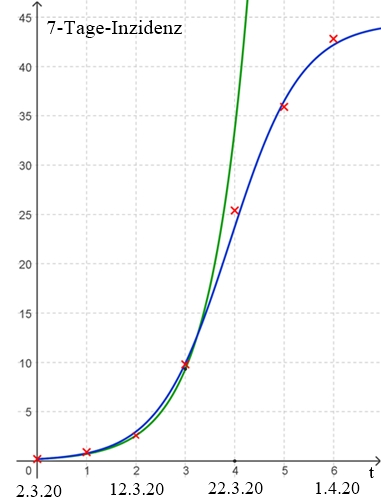
Entwicklung der 7-Tage-Inzidenz des Coronavirus
in Deutschland von 2.3.2020 bis 1.4.2020

 7-Tage-Inzidenz

0,2

0,9

2,8

9,8

25,4

35,9

42,8

 Zeit t

0

1

2

3

4

5

6

 Datum

2.3.2020

7.3.2020

12.3.2020

17.3.2020

22.3.2020

27.3.2020

1.4.2020

1 Zeiteinheit für t entspricht 5 Tage, Maximum der 7-Tage-Inzidenz bis 9/2020 am 4.4.2020: 44,5,   Quelle: RKI

Exponentielle Näherung:  f(t) = 0,2٠3,6 t (grün),

Logistische Näherung:      g(t) =    (blau)

 

Graphische Darstellung von f(t) und g(t) in Abhängigkeit von der Zeit
Die 7-Tage-Inzidenz-Werte sind als rote Punkte dargestellt

 

Radioaktiver Zerfall

Das Zerfallsgesetz für die Aktivität A(t) eines radioaktiven Präparats zum Zeitpunkt t lautet:

A(t) = A(0)٠e - λ٠t ,  A(0) = Aktivität zum Zeitpunkt t = 0,  λ heißt Zerfallskonstante.

Die Einheit der Aktivität ist 1 Bq (Becquerel) = 1 radioaktiver Zerfall pro Sekunde.

Zusammenhang zwischen Halbwertszeit T½  und  λ: 

½ A(0) = A(0)٠e - λ٠T½  ⇒ ln ½ = - λ٠ T½   und  ln ½ = - ln 2, daraus folgt:

 λ =,  ln 2 ≈ 0,6931

(ln = natürlicher Logarithmus = Logarithmus zur Basis e ≈ 2,71828)

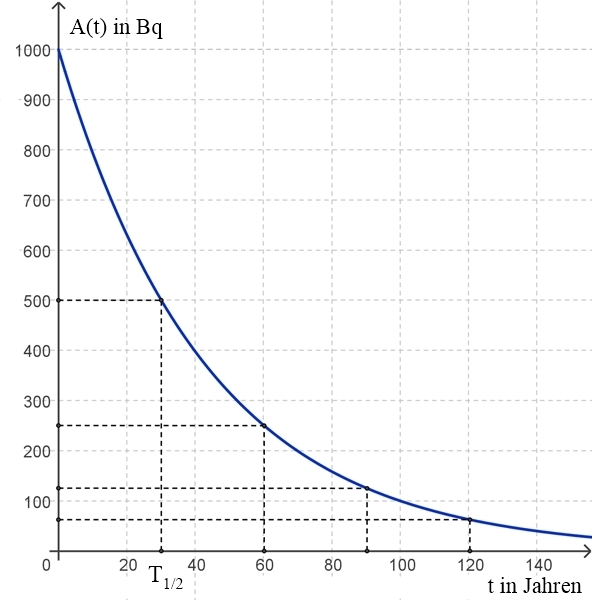
Beispiel:

Caesium-137:  T½ = 30,1 Jahre (u.a. freigesetzt bei der Reaktorkatastrophe von Tschernobyl)

A(t) = A(0)٠e -λ٠t , A(0) = 1000 Bq,  λ ≈ 0,02303 1/Jahre, t in Jahren

Graphische Darstellung der Aktivität A(t) in Abhängigkeit von der Zeit t

 

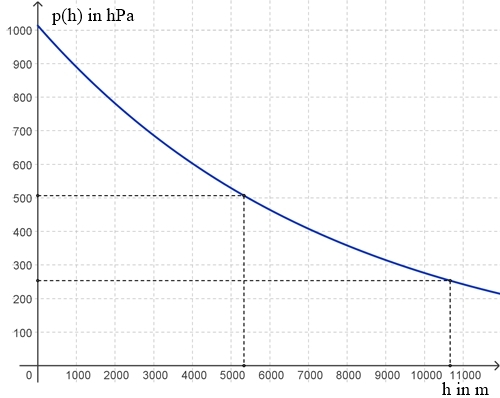
Exponentielle Abnahme des Luftdrucks

Der absolute Luftdruck p(h) nimmt mit der Höhe h exponentiell ab und zwar um ca. 0,01284% pro m (Meter).

Luftdruck in Höhe h = 1 m: 100% - 0,01284% = 99,98716% von 1013,25 hPa.

Bei jedem weiteren Meter nimmt der Luftdruck um das 0,9998716-fache ab.

p(h) = p(0) ٠ 0,9998716 h , p(0) = 1013,25 hPa (Hektopascal)

1013,25 hPa ist der Luftdruck auf Meeresniveau.

Einheiten: 1 Pa = 1 N/m², 1 hPa = 1 mbar, 1013,25 hPa ≈ 1 bar

Höhe in m

1000

2000

3000

4000

5000

5398

Luftdruck in hPa

891

784

689

606

533

p(0)/2

Auf der Zugspitze h = 2962 m ergibt sich als Luftdruck:

p(2962)= 1013,25 ٠ 0,9998716 2962 = 1013,25 ٠ 0,683625 = 692,7 hPa

692,7 hPa von 1013,25 hPa sind 68,4%

Auf dem Mount Everest h = 8848 m ergibt sich als Luftdruck:

p(8848)= 1013,25 ٠ 0,9998716 8848 = 1013,25 ٠ 0,32105 = 325,3 hPa

325,3 hPa von 1013,25 hPa sind 32,1%
 

Graphische Darstellung des Luftdrucks p(h) in Abhängigkeit von der Höhe h

 

Zurück
Zurück zur Startseite