Exponentalfunktionen

Die allgemeine Exponentalfunktion

x wird abgebildet auf y = f(x)  mit der Gleichung: 
f(x) = a^x , x  ℝ (x ist Element der reellen Zahlen, a > 0)

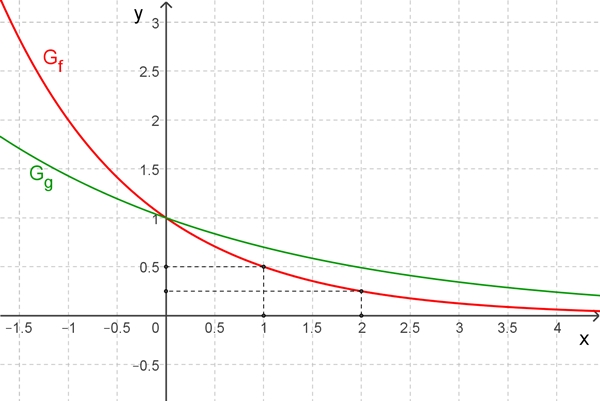
1. Beispiel a > 1:  f(x) = 1,2^x, g(x) = 1,5^x, h(x) = 2^x

Graphische Darstellung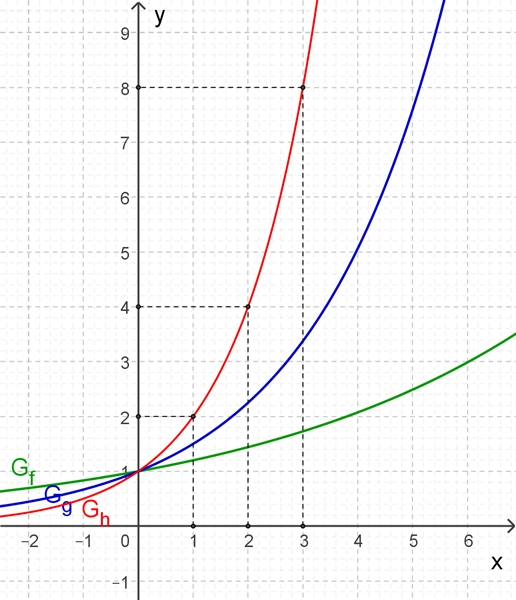

Bei h(x) = 2^x ergibt sich für x = 1, 2, 3, … y = 2¹ = 2, 2² = 4, 2³ = 8, …

Das bedeutet, dass bei gleichem zeitlichen Abstand 1 der Wert von y sich verdoppelt, vervierfacht, verachtfacht, usw., d.h. der Wert von y nimmt um den Faktor 2¹, 2², 2³ . . . exponentiell zu.

Bei jeder Exponentialfunktion gilt für a > 1 (Wachstumsfunktion):

Bei zunehmend gleichem Abstandswert Δx verdoppelt sich jeweils der Wert von y.

Die Funktion h hat ein stärkeres exponentielles Wachstum als die Funktion g.

 
2. Beispiel 0 < a < 1:  f(x) = 0,5^x, g(x) = 0,7^x

Graphische Darstellung

Bei jeder Exponentialfunktion gilt für 0 < a < 1 (Zerfallsfunktion):

Bei zunehmend gleichem Abstandswert Δx halbiert sich jeweils der Wert von y.

Die Funktion f hat eine stärkere exponentielle Abnahme als die Funktion h.

Die natürliche Exponentalfunktion

x wird abgebildet auf y = f(x)  mit der Gleichung   
f(x) = e^x , x  ℝ (x ist Element der reellen Zahlen)

e ≈ 2,718281828 (Eulersche Zahl)

Darstellung des Graphen G_f der natürlichen Exponentalfunktion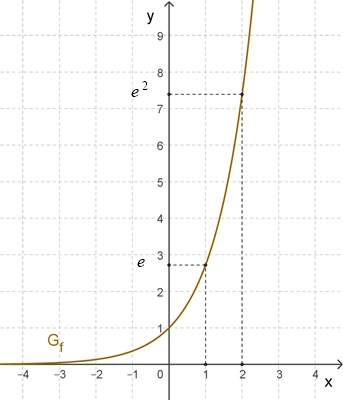

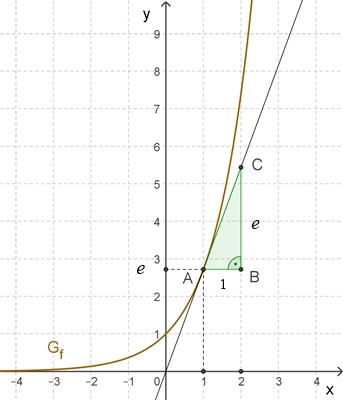
Für x = 1, 2, 3, … ergibt sich y = e, e², e³, … (exponentielles Wachstum)

Für die natürliche Exponentialfunktion gilt: 
Die Steigung an der Stelle x ist gleich dem Funktionswert an der Stelle x, kurz:  f ‘(x) = f(x) ⇔  e^x = e^x

Beispiel:  

f(1) = e,
f ‘(1) = e, entspricht der Steigung   = e : 1  im Steigungsdreieck ABC.

Die Umkehrfunktion zu f(x) = e^x , x  ℝ

f ^-1(x) = log_e x = ln x,  x  ℝ⁺  heißt natürliche Logarithmusfunktion,  wobei gilt:

ln e^x = x,  für x = 1 gilt  ln e = 1  (log_e x  = Logarithmus von x zur Basis e, ln x = natürlicher Logarithmus von x)

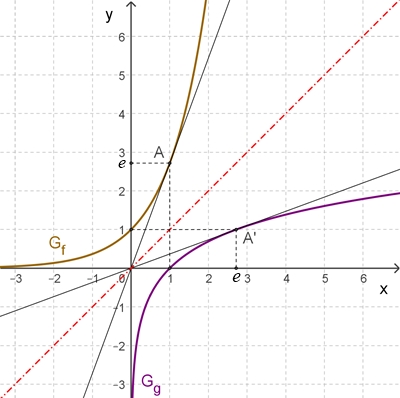
Darstellung des Graphen G_f der natürlichen Exponentalfunktion und seiner Umkehrfunktion G_g  mit g = f ^-1

Rechenregeln:

a^x = e^{x٠ln a}   ⇔  ln a^x = ln e^{x٠ln a}   ⇔  ln a^x = x٠ln a

Andere Schreibweise der allgemeinen Exponentialfunktion:

f(x) = e^{x٠ln a} =  e^k٠x , x  ℝ  mit k = ln a und a > 0

Für die Ableitung gilt:

f ‘(x) = k٠e^k٠x, x  ℝ