Dezimalsystem (Zehnersystem)

Im Zehnersystem gibt es die 10 Ziffern  0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Beispiele: 

a) Ganze Dezimalzahl

H = Hundert(er), Z = Zehn(er), E = Eine(r)

1٠10⁹ + 3٠10⁸ + 8٠10⁷ + 4٠10⁶ + 7٠10⁵ + 2٠10⁴ + 0٠10³ + 5٠10² + 7٠10¹ + 3  =  = 1 384 720 573

Eine Milliarde dreihundertvierundachtzig Millionen siebenhundertzwanzigtausend fünfhundertdreiundsiebzig

10¹²  = Billion, 10¹⁵  = Billiarde, 10¹⁸  = Trillion, 10²¹  = Trilliarde, 10²⁴  = Quadrillion, 10²⁷  = Quadrilliarde, . . .

Vorsicht!  1 billion (USA) = 1 Milliarde, 1 trillion (USA) = 1 Billion

b) Dezimalbruch

z = zehntel, h = hundertstel, t = tausendstel, zt = zehntausendstel,

Abkürzung	H	Z	E	z	h	t	zt
Stellenwert	102	101	1=100	10-1	10-2	10-3	10-4
Ziffer	1	4	5	3	0	7	2

1٠10² + 4٠10¹ + 5 + 3٠10^-1 + 0٠10^-2 + 7٠10^-3 + 2٠10^-4  =  145,3072

ht = hunderttausendstel (10^-5) , m = millionstel (10^-6), . . .

Dualsystem (Binärsystem, Zweiersystem)

Im Dualsystem gibt es nur die beiden Ziffern  0 und 1

Beispiele:

a) Ganze Dualzahl

Stellenwert	28	27	26	25	24	23	22	21	1=20
Ziffer	0	1	1	0	1	0	1	1	1

   1011010111₂  (Dualzahl mit Index 2 gekennzeichnet) =

= 1٠2⁷ + 1٠2⁶ + 0٠2⁵ + 1٠2⁴ + 0٠2³ + 1٠2² + 1٠2¹ + 1  =

=  128 + 64 + 16 + 4 + 2 + 1  =  215

b) Dualbruch

Stellenwert	22	21	20	2-1	2-2	2-3	2-4
Ziffer	1	0	1	1	0	1	1

    101,1011₂ =
=  1٠2² + 0٠2¹ + 1 + 1٠2^-1 + 0٠2^-2 + 1٠2^-3 + 1٠2^-4  = 

= 5 + 1/2 + 1/8 + 1/16  =  5 + 11/16  = 5,6875

Die Addition, Subtraktion, Multiplikation und Division erfolgt bei den Dualzahlen wie bei den Dezimalzahlen, wobei gilt:

0 + 0 = 0, 1 + 0 = 0 + 1 = 1, 1 + 1 = 10  und 0٠0 = 0, 1٠0 = 0٠1 = 0, 1٠1 = 1

Beispiel für die Addition:

Stellenwert	64	32	16	8	4	2	1	Dezimal
Dual		1	0	1	0	1	0	42
+			1	1	1	1	1	31
Übertrag		1	1	1	1
	1	0	0	1	0	0	1	73

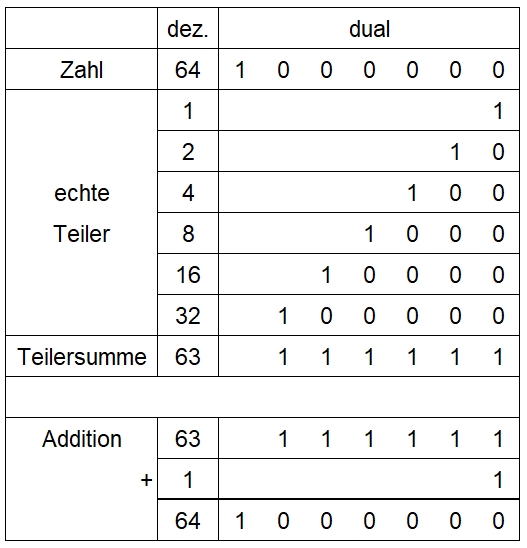
Addition der echten Teiler von Zweierpotenzen

Addition der echten Teiler von 64 = 2⁶ im Dezimal- und Dualsystem

Entsprechend erfolgt die Addition der echten Teiler von 2ⁿ für n = 1, 2, 3, . . .

Vergleich der ersten 15 Zahlen im Dezimal-, Dual-, Ternär (Dreier)- und  Hexadezimalsystem (16er System):

185  =  10111001₂  =  20212₃  =  B9_hex  (Hexadezimalzahl mit Index hex)

255  =  11111111₂  =  FF_hex 

Eine Zahl kann im Hexadezimalsystem deutlich kürzer als im Dualsystem dargestellt werden.

Die Bedeutung der Dualzahlen beim Computer

Ein Computer wird mit binären Operationen gesteuert.
Im Computer (Prozessor, Arbeitsspeicher, Daten- und Adressbus, Betriebssystem) und auch bei der Ein- und Ausgabe von Daten werden Dualzahlen verwendet. Sie werden jedoch meist in Form von Hexadezimalzahlen dargestellt.
Jede Speicherung von Daten erfolgt technisch als Dualzahl. Das heißt, jeglicher Datensatz (Text, Bilder, Audio, Video) wird in eine meist lange Reihe von Einsen und Nullen umgewandelt. Ein Computerprogramm entscheiden darüber, was der Strom von Nullen und Einsen schließlich darstellen soll.
Computer können inzwischen eine sehr große Zahl an Bits (0 oder 1) im Arbeitsspeicher speichern oder im Prozessor verarbeiten.

Bespiel:    Arbeitsspeicher 8 GB (Gigabyte) = 64 000 000 000 Bit
                 64-Bit Betriebssystem, 64-Bit Prozessor

Der ASCII-Code

Zur Eingabe und Ausgabe von Daten wurden Steuerzeichen, Buchstaben und Symbole im ASCII-Standard (American Standard Code for Information Interchange) zunächst mit einem 7-Bit-Code (128 verschiedene Zeichen als 7stellige Dualzahlen) verwendet , dann mit einem erweiterten 8-Bit-Code (8 Bits = 1 Byte, 256 verschiedene Zeichen als 8stellige Dualzahlen), dargestellt mit verschiedenen Codepages bei MS-DOS für verschiedene Regionen. Die 256 verschiedenen Darstellungen im erweiterten ASCII-Code reichen als Dualzahl von 00000000 bis 11111111 (dezimal von 0 bis 255).
Die ersten 32 Codes stellen Steuerzeichen für den Computer dar.
Beispiele:  Backspace   =  00001000₂ = 08_hex   = 8 (Cursor eine Position zurück)
                  Buchstabe A = 01000001₂ = 41_hex  = 65
                  Buchstabe  a = 01100001₂ = 61_hex  = 97

Unicode

Unicode wurde mit dem Ziel geschaffen, als einheitlicher Standard für die Darstellung  sämtlicher von Menschen entwickelter Schriftsysteme und Zeichen zu dienen.
Der gesamte vom Unicode-Standard (32-Bit pro Zeichen) beschriebene Bereich umfasst 1 114 112 mögliche Zeichen (0000_hex bis 10FFFF_hex), bisher (2020) wurden 143 859 verschiedene Buchstaben und Zeichen dargestellt bzw. codiert.

Maschinencode

Der binäre Maschinencode steuert die Rechenvorgänge im Computer.
Die Eingabe der Befehle kann auch durch einen Assembler erfolgen, der die Eingabe vereinfacht.
Die Programmierarbeit wird aber durch die modernen Programmiersprachen wesentlich erleichtert.