Zyklische Gruppen und zyklische Zahlen

1. Definitionen und wichtige Sätze

Definition1:  Eine Gruppe G, die nur aus den Potenzen g, g², g³, ... gⁿ = e eines Elementes g
                       besteht, heißt zyklische Gruppe Z_n der Ordnung n.
                       Ein Element g, aus dessen Potenzen Z_n besteht, heißt erzeugendes Element von Z_n.

Bemerkung:  Z_n = {e, g, g², g³, ... g^{n - 1}} mit Einselement e = gⁿ  und der Abkürzung  g² = g  g 
                       usw. bezüglich der Verknüpfung  .

Satz 1:          Zu jeder natürlichen Zahl n gibt es genau eine zyklische Gruppe der Ordnung n. 
                      Sie ist kommutativ und isomorph zur additiven Restklassengruppe modulo n.

Satz 2:         Es sei G eine von g erzeugte zyklische Gruppe. Dann gelten die folgenden Aussagen:
                     a)  Jede Untergruppe U von G ist zyklisch.
                     b)  Hat G ={e, g, g², g³, ... g^{n - 1}} die Ordnung n, so gibt es zu jeder natürlichen 
                          Zahl d, die n teilt, genau eine zyklische Untergruppe U_d der Ordnung d von G,   

                          die von erzeugt wird.

Definition2:  Der Nenner eines gewöhnlichen Bruches sei eine Primzahl. Die Perioden des 
                      zugehörigen Dezimalbruches werden als zyklische Zahlen bezeichnet, wenn 
                      die Periodenlänge gleich der Primzahl im Nenner minus 1 ist.

Bemerkung:  Von den Primzahlen unter 100 erzeugen die neun Primzahlen 7, 17, 19, 23, 29, 
                       47, 59, 61 und 97 zyklische Zahlen.

Definition3:  Die Eulersche Funktion (m) gibt die Anzahl der zu m teilerfremden Zahlen 
                      zwischen 1 und m an.

Bemerkung:  Falls p eine Primzahl ist,  gilt: (p) = p – 1.

Definition4:   Zwei ganze Zahlen a, b heißen kongruent modulo m, wenn sie bei Division 
                       durch m denselben Rest haben.
                       Schreibweise:  a  b  mod  m

Definition5:   Die Ordnung t von a mod m, i.Z. ord_m(a) = t, ist die kleinstmögliche Zahl t 
                       für die gilt:   a^t 1  mod  m.

Satz3:            Es sei m eine natürliche Zahl mit ggT(m,10) = 1 und ord_m(10) = t. Die (m) Brüche
                        mit 1  a < m  und  ggT(a,m) = 1  bilden dann     Klassen mit jeweils t 
                       Elementen, so dass die Perioden der Dezimalbruchentwicklungen der Brüche in  
                       einer Klasse durch zyklische Vertauschung auseinander hervorgehen.

2. Beispiele für zyklische Gruppen der Ordnung 6

a)  Die Restklassengruppe modulo 6 bezüglich der Addition als Verknüpfung

Zyklische Gruppe der Ordnung 6:

Z₆= {e, g , g², g³, g⁴, g⁵ } = {0, 1, 2, 3, 4, 5}, erzeugendes Element 1 (I)
                                          = {0, 5, 4, 3, 2, 1}, erzeugendes Element 5 (II)

Zyklische Untergruppen:

Z₃ = {e , g , g² } = {0, 2, 4}, erzeugendes Element 2 
                            = {0, 4, 2}, erzeugendes Element 4 

Z₂ = {e , g } = {0 , 3}, erzeugendes Element 3 

Verknüpfungstafel (Gruppentafel)  bezüglich der Addition als Verknüpfung ,
darunter jeweils Verknüpfungstafeln der Untergruppen:

+ 0 1 2 3 4 5 0 0 1 2 3 4 5 1 1 2 3 4 5 0 2 2 3 4 5 0 1 3 3 4 5 0 1 2 4 4 5 0 1 2 3 5 5 0 1 2 3 4
+ 0 2 4 0 0 2 4 2 2 4 0 4 4 0 2	+ 0 3 0 0 3 3 3 0

 

b)  Die Restklassengruppe modulo 7 bezüglich der Multiplikation als Verknüpfung

Zyklische Gruppe der Ordnung 6:

Z₆= {e, g , g², g³, g⁴, g⁵ } = {1, 3, 2, 6, 4, 5}, erzeugendes Element 3 (III)
                                          = {1, 5, 4, 6, 2, 3}, erzeugendes Element 5 (IV)

                                               z.B. 3² mod 7 = 9 mod 7 = 2 mod 7

Zyklische Untergruppen:

Z₃ = {e , g , g² } = {1, 2, 4} , erzeugendes Element 2
                             = {1, 4, 2} , erzeugendes Element 4

Z₂ = {e , g } = {1 , 6}, erzeugendes Element 6

Verknüpfungstafel (Gruppentafel) im Fall (III)  (links) und im Fall (IV)  (rechts),
darunter jeweils die Verknüpfungstafeln der Untergruppen:  

* 1 3 2 6 4 5 1 1 3 2 6 4 5 3 3 2 6 4 5 1 2 2 6 4 5 1 3 6 6 4 5 1 3 2 4 4 5 1 3 2 6 5 5 1 3 2 6 4	* 1 5 4 6 2 3 1 1 5 4 6 2 3 5 5 4 6 2 3 1 4 4 6 2 3 1 5 6 6 2 3 1 5 4 2 2 3 1 5 4 6 3 3 1 5 4 6 2
* 1 2 4 1 1 2 4 2 2 4 1 4 4 1 2	* 1 6 1 1 6 6 6 1

 

c) Die von der Primzahl 7 erzeugten zyklischen Zahlen

Die Abbildung   Z₆ liefert je nach erzeugendem Element eine zyklische Linksverschiebung oder ein eine zyklische Rechtsverschiebung.

k mod 7   k  {1, 2, 3, 4, 5, 6}

          1 

          2 

          3 

          4 

          5 

          6 

Z₆ mit  g = 3  als erzeugendem Element liefert eine zyklische Linksverschiebung:

          1 

          3 

          2 

          6 

          4 

          5 

Z₆ mit  g = 5  als erzeugendem Element liefert eine zyklische Rechtsverschiebung:

          1 

          5 

          4 

          6 

          2 

          3 

Zuordnung bei der zyklischen Gruppe der Ordnung 6 bezüglich der Multiplikation mit Linksverschiebung mit den erzeugenden Elementen 10 und 3 :

10⁰  mod 7  3⁰  mod 7  1 

10¹  mod 7  3¹  mod 7  3 

10²  mod 7  3²  mod 7  2 

10³  mod 7  3³  mod 7  6 

10⁴  mod 7  3⁴  mod 7  4 

10⁵  mod 7  3⁵  mod 7  5 

10⁶  mod 7  3⁶  mod 7  1 
 

Erzeugung einer zyklischen Linksverschiebung:

Eine Stelle nach links:

  , wobei gilt: 10   3 mod 7

Zwei Stellen nach links:

  , wobei gilt: 10² 3²   2 mod 7

Drei Stellen nach links:

  , wobei gilt: 10³ 3³   6 mod 7

usw.
 

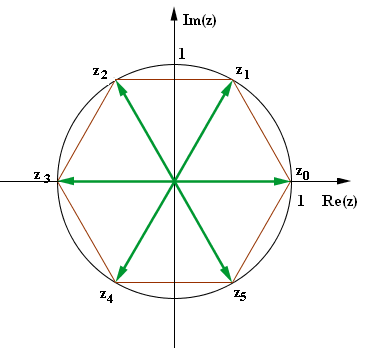
d)  Die zyklische Gruppe der 6-ten Einheitswurzeln bezüglich der Multiplikation als Verknüpfung

Kreisteilungsgleichung  z ⁶ = 1, z 

Lösungen:  ,   k  {0, 1, 2, 3, 4, 5}

Zyklische Gruppe der Ordnung 6:

Z₆= {e, g , g², g³, g⁴, g⁵ } = {1, z₁, z₂, z₃, z₄, z₅ }   Linksdrehung
                                           = {1, z₅, z₄, z₃, z₂, z₁ }  Rechtsdrehung

Zyklische Untergruppen:

Z₃ = {e , g , g² } = {1, z₂, z₄ }  Linksdrehung
                            = {1, z₄, z₂ }  Rechtsdrehung

Z₂ = {e , g } = {1 , z₃ }

Verknüpfungstafel (Gruppentafel) bei Linksdrehung wie Fall b) (I) (hier dargestellt), entsprechend Rechtsdrehung bei Fall b) (II) 
  

*	z0	z1	z2	z3	z4	z5
z0	z0	z1	z2	z3	e4	z5
z1	z1	z2	z3	z4	z5	z0
z2	z2	z3	z4	z5	z0	z1
z3	z3	z4	z5	z0	z1	z2
z4	z4	z5	z0	z1	z2	z3
z5	z5	z0	z1	z2	z3	z4

Literatur

B. Hornfeck, Algebra. Walter de Gruyter & Co, Berlin (1969).

Lugowksi-Weinert, Grundzüge der Algebra Bd.I. Pfalz-Verlag Basel (1968).

H. Scheid, Elemente der Arithmetik und Algebra. BI Wissenschaftsverlag, Mannheim (1992).

F. Padberg, Elementare Zahlentheorie. BI Wissenschaftsverlag, Mannheim (1991).

R. Domine, Periodische Systembrüche. Praxis der Mathematik 3/35 (1993).