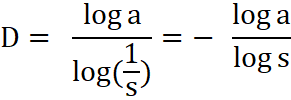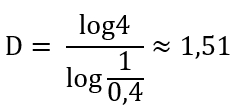|
Fraktale Bei Fraktalen handelt es sich um geometrische Figuren, deren Struktur stark zerklüftet erscheint. Die Vergrößerung eines Ausschnitts eines Fraktals liefert wieder eine ähnliche Struktur. Man spricht von Selbstähnlichkeit.Dimension D der Selbstähnlichkeit (Ähnlichkeit):
a = Anzahl der selbstähnlichen Teile, s = Verkleinerungsfaktor < 1 Bei Fraktalen ist die Dimension der Selbstähnlichkeit meist ungleich einer natürlichen Zahl.
Beispiele für Fraktale
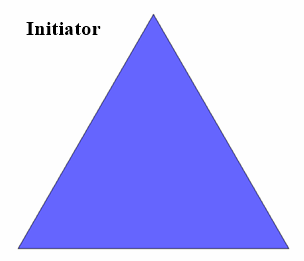
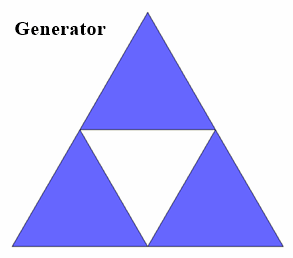
Bei einem Dreieck werden die Mittelpunkte der Seiten verbunden und das so entstandene mittlere Dreieck entfernt (Generator).
Es bleiben so 3 Dreiecke übrig, deren Seiten jeweils halb so lang sind. Die Dimension der Selbstähnlichkeit ist mit a = 3 und s = 1/2:
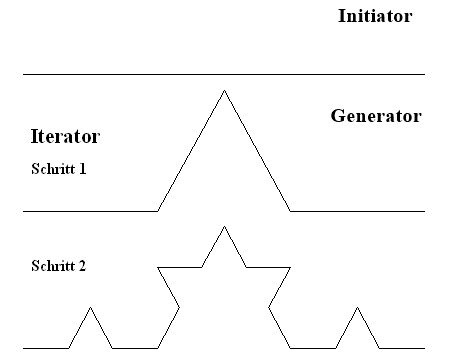
Ausgangspunkt für die Koch-Schneeflocke ist
die Seite eines gleichseitigen Dreiecks.
Diese Strecke wird nun im 1. Iterationsschritt durch vier Seiten ersetzt,
die jetzt 1/3 der Länge der ursprünglichen Strecke haben (Generator).
Der schwedische Mathematiker Helge
von Koch hat 1904 gezeigt, dass die bei dieser Iteration für
n gegen ∞
entstehende Kurve überall stetig aber nirgends differenzierbar ist.
Die Dimension der Selbstähnlichkeit ist mit a = 4 und s = 1/3
Hilbert-Kurve
Ausgangspunkt (Initiator) für die Hilbert-Kurve sind drei Seiten eines
Quadrats.
Der deutsche Mathematiker David
Hilbert entdeckte 1891, dass die bei dieser Iteration für n gegen ∞
entstehende stetige Kurve, die Fläche eines Quadrats vollständig ausfüllt.
Die Dimension der Selbstähnlichkeit ist mit a = 4 und s = 1/2
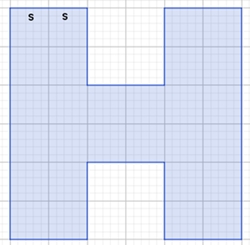
H-Fraktal
Initiator
Generator
Inhalt der
gefärbten H-Fläche im Vergleich zum Inhalt des Umfangsquadrats beim
Die H
begrenzende Kurvenlänge beim Initiator ist 22 s, beim Generator 44 s.
Dann gilt bei
der Iteration für n gegen ∞, dass der gefärbte Flächeninhalt im Vergleich
zum Umfangsquadrat 7/9 ist und die begrenzende Kurvenlänge gegen ∞ geht.
Die
Dimension D der Selbstähnlichkeit ist mit a = 4 und dem
Verkleinerungsfaktor ½
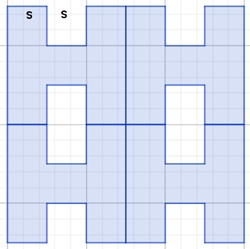
Quadrat-Fraktal
Initiator
Generator
Flächeninhalt A1 des Ausgangsquadrats
(Initiator): a2.
Flächeninhalt A2 der 4 Quadratflächen des
Generators: 4٠0,16 a2 = 0,64 a2.
Flächenverhältnis A2/A1 = 0,64
Die Kurvenlänge beim Initiator ist 4a, beim
Generator: 4٠1,6a = 6,4a.
Bei jedem Iterationsschritt nimmt der
Flächeninhalt um den Faktor 0,64 ab, die Kurvenlänge um den Faktor 1,6 zu.
Dann gilt bei der Iteration für n gegen ∞,
dass der blau gefärbte Flächeninhalt im Vergleich zum Umfangsquadrat gegen 0
und die begrenzende Kurvenlänge gegen ∞ geht.
Die Dimension D der Selbstähnlichkeit
ist mit a = 4 und dem Verkleinerungsfaktor s = 0,4
Zu den Fraktalen zählen im weiteren Sinne auch
Julia-Mengen und die
Mandelbrot-Menge.
Durch Iterationen wurden folgende Bilder erzeugt:
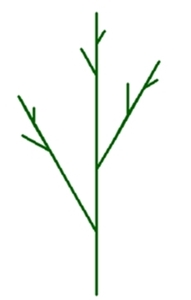
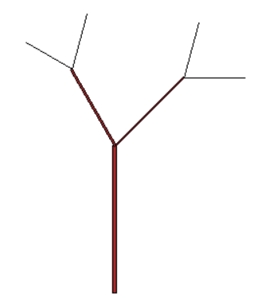
Strauch als Fraktal:
1. Iteration
3. Iteration
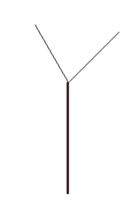
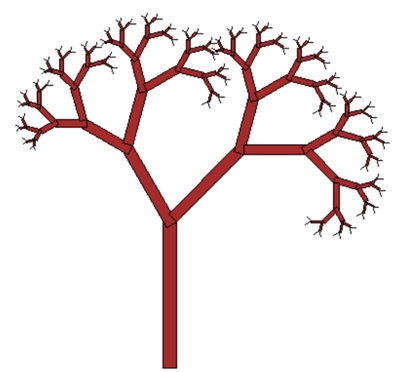
Baum als
Fraktal:
1. Iteration
5. Iteration
Fraktalähnlicher Wald im Frühjahr und im
Herbst:
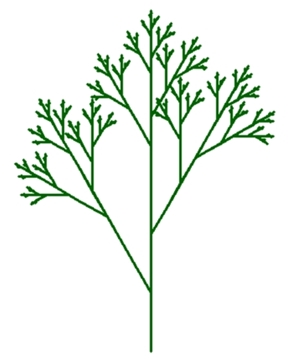
Farn als Fraktal
erzeugt mit IFS (iteriertes Funktionensystem):
Die Natur liefert viele Beispiele von
Fraktalen oder fraktalähnlichen Gebilden:
Dentriten, Blutgefäße, Schneeflocken, Gemüse
(z.B. Brokoli, Blumenkohl), Pflanzen, Sträucher, Bäume, Korallen, Berge,
Wolken, Blitze ...
Die Bilder wurden mit der Programmiersprache Python
erzeugt. |