Lehrsätze im Dreieck

1a) Winkelsumme im Dreieck

Satz von der Winkelsumme im Dreieck:

In jedem Dreieck beträgt die Summe der Größen der Innenwinkel 180°.
                α + β + γ = 180°

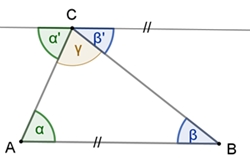
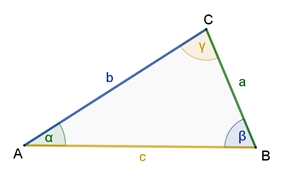
Begründung:

An der Parallelen zur Geraden AB durch C liegen am Punkt C die drei Winkel  α´, γ und β´ an, die sich zu 180° (gestreckter Winkel) addieren:  α´+ γ + β´ = 180°.

α´ = α  und  β´ = β  sind gleich große Wechselwinkel an Parallelen.

Daraus folgt dann auch für die Summe der Winkel α, β und γ:  α + β + γ = 180°

1b) Winkelsumme in Vielecken

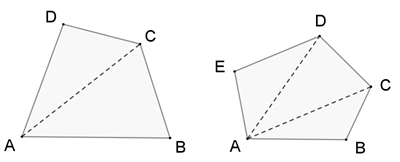
Ein Viereck lässt sich in zwei Dreiecke unterteilen. Damit ist die Winkelsumme
2٠180° = 360°.
Ein Fünfeck lässt sich in drei Dreiecke unterteilen. Damit ist die Winkelsumme
3٠180° = 540°.
Allgemein gilt: Die Winkelsumme im n-Eck beträgt (n-2)٠180° 

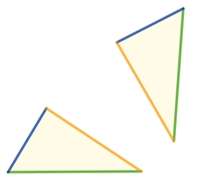
2)  Kongruenzsätze für Dreiecke

Zwei deckungsgleiche Figuren F und G nennt man zueinander kongruent, i.Z. F ≅ G. Sie stimmen in allen entsprechenden Stücken, wie z.B. Seiten und Winkel, überein.

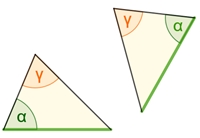
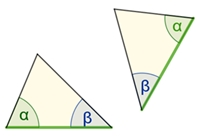
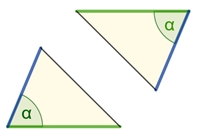
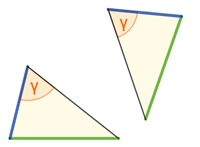
Zwei Dreiecke sind zueinander kongruent (deckungsgleich), wenn sie in allen drei Seiten übereinstimmen (SSS-Satz),

in einer Seite und zwei gleichliegenden Winkeln übereinstimmen (WSW- und SWW-Satz),

               in zwei Seiten und dem eingeschlossenem Winkel übereinstimmen (SWS-Satz),

              in zwei Seiten und dem Gegenwinkel der längeren Seite übereinstimmen (SsW-Satz).

Begründung:

Die Kongruenzsätze folgen aus der eindeutigen Konstruktion des Dreiecks durch die gegebenen übereinstimmenden Größen.

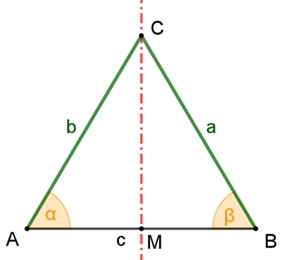
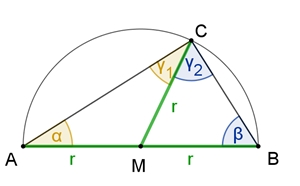
3)  Das gleichschenklige Dreieck

 Satz vom gleichschenkligen Dreieck
Trifft für ein Dreieck eine der folgenden Aussagen zu, so gelten auch die beiden anderen:
a) Das Dreieck ist gleichschenklig (hier: a = b).
b) Das Dreieck ist achsensymmetrisch.
c) Das Dreieck besitzt zwei gleich große Winkel  
    (hier: α = β)

4)  Das rechtwinklige Dreieck

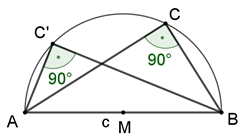
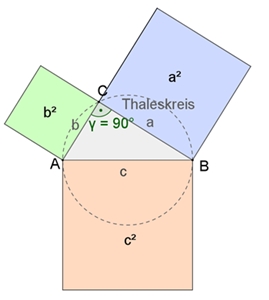
Satz des Thales:
Ein Dreieck ABC hat genau dann bei C einen rechten Winkel, wenn die Ecke C auf dem Halbkreis über [AB] liegt.

Begründung:

Die Dreiecke AMC und MBC sind gleichschenklig mit den gleich langen Seiten [AM], [MC] und [MB].
Daher gilt:  α  = γ₁  und  β = γ₂ .
Für die Winkelsumme im Dreieck ABC gilt:
γ₁ + γ₁ + γ₂ + γ₂ = 180°
2٠(γ₁ + γ₂) = 180°  oder  γ₁ + γ₂  =  90°

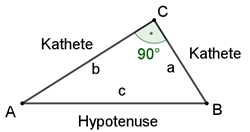
Im rechtwinkligen Dreieck heißen die dem rechten Winkel anliegenden Seiten (hier a und b) Katheten und die dem rechten Winkel gegenüberliegende Seite (hier: c) Hypotenuse.

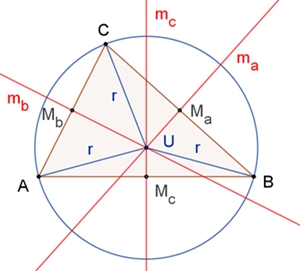
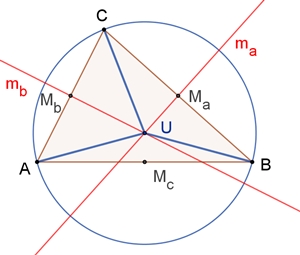
5)  Mittelsenkrechten und Umkreis

Satz von den Mittelsenkrechten im Dreieck

Die drei Mittelsenkrechten der drei Seiten eines Dreiecks schneiden sich in einem Punkt, dem Umkreismittelpunkt U des Dreiecks.
Der Punkt U hat von den drei Ecken des Dreiecks den gleichen Abstand r.

Begründung:

Die beiden Mittelsenkrechten m_a und m_b schneiden sich im Punkt U.
Dann sind die Dreiecke BCU und CAU jeweils gleichschenklige Dreiecke mit gleich langen Seiten
[BU], [CU] und [AU].
Da  |AU| = |BU|  folgt, dass die Symmetrieachse des gleichschenkligen Dreiecks ABU auch durch den Punkt U geht.

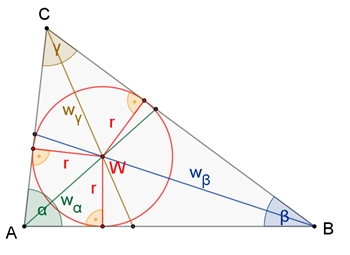
6)  Winkelhalbierende und Inkreis

Satz von den Winkelhalbierenden im Dreieck

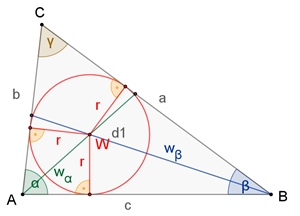
Die drei Winkelhalbierenden der drei Winkel eines Dreiecks schneiden sich in einem Punkt, dem Inkreismittelpunkt W des Dreiecks.

Der Punkt W hat von den drei Seiten des Dreiecks den gleichen Abstand r.

Begründung:

Die beiden Winkelhalbierenden bilden die  Symmetrieachsen von α und β und schneiden sich im Punkt W.
W hat dann von c und a und auch von c und b gleichen Abstand. W hat aber dann auch von a und b gleichen Abstand.
Daraus folgt, dass W auch auf der Winkelhalbierenden von γ liegen muss.

 

7)  Höhen im Dreieck

Satz von den Höhen im Dreieck

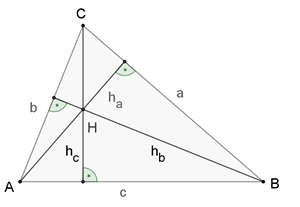
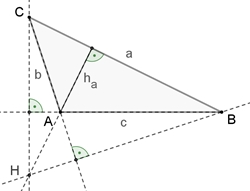
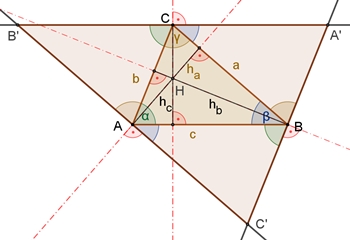
Im Dreieck schneiden sich die drei Höhen oder deren Verlängerungen in einem Punkt, dem Höhenschnittpunkt H des Dreiecks.

Begründung:

A´B´ ist parallel zu AB, A´C´ ist parallel zu AC und B´C´ ist parallel zu BC.
Die Dreiecke ABC, AC´B, CBA´ und BÁC sind zueinander kongruent (Wechselwinkel an Parallelen und WSW-Satz). Dann sind auch entsprechende Seiten der Dreiecke gleich lang und damit A, B und C Mittelpunkte der Seiten des Dreiecks A´B´C´. Die Höhen des Dreiecks ABC liegen deshalb auf den Mittelsenkrechten des Dreiecks A´B´C´ und schneiden sich damit in einem Punkt.

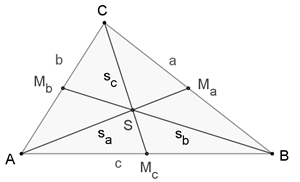
8)  Seitenhalbierende des Dreiecks

Satz von den Seitenhalbierenden im Dreieck

Im Dreieck schneiden sich die Seitenhalbierenden in einem Punkt, dem Schwerpunkt S des Dreiecks.
Der Schwerpunkt teilt die Seitenhalbierenden im Verhältnis 2 : 1.

        Begründung:

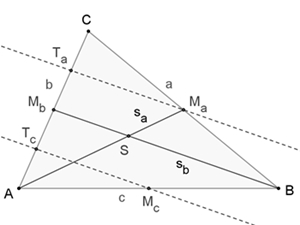
Die Parallelen zu s_b durch M_a und M_c schneiden b in den Punkten T_a und T_c.
Nach dem 1. Strahlensatz (Kap  ) mit dem Zentrum A ist T_c die Mitte der Strecke AM_b, da M_c Mitte der Strecke AB ist. Ebenso ist T_a Mitte der Strecke M_bC. damit teilen die Punkte T_c, M_b und T_a die Strecke AC in vier gleiche Teile.
Dann gilt nach dem 1. Strahlensatz
|AS| : |SM_a| = |AM_b| : | M_bT_a| = 2 : 1
Analog gilt auch für die Seitenhalbierende s_a  |BS| : |SM_b| = 2 : 1.

Für den Schnittpunkt von s_a und s_c gilt dasselbe, also muss es einen gemeinsamen Schnittpunkt für die Seitenhalbierenden geben.

Zusammenhang zwischen Umkreismittelpunkt U, Höhenschnittpunkt H und Schwerpunkt S des Dreiecks siehe
Euler-Gerade und Feuerbach-Kreis

 9)  Zentrische Streckung, Strahlensatz und ähnliche Figuren

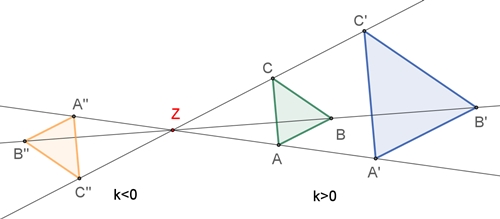
Bei einer zentrischen Streckung mit dem Zentrum Z und dem Streckfaktor k gilt für den Bildpunkt P´ zu einem Punkt P (P ≠ Z):
I   P´ liegt auf der Gerade ZP
II  |ZP´| = k٠|ZP|

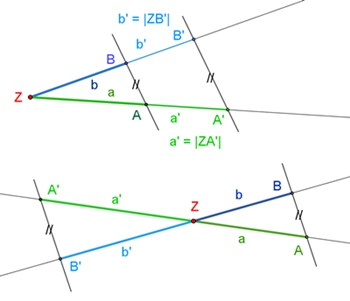
Strahlensatz

1. Werden zwei sich in Z schneidende Geraden von zwei Parallelen außerhalb von Z geschnitten, so verhalten sich je zwei Abschnitte auf der einen Geraden wie die entsprechenden Abschnitte auf der anderen Geraden   a : a´ =  b : b´

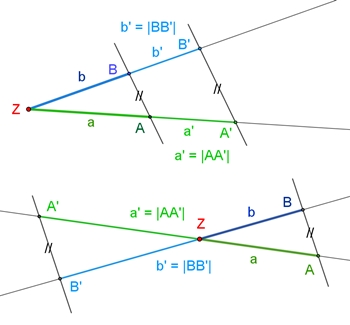
2. Werden zwei sich in Z schneidende Geraden von zwei Parallelen außerhalb von Z geschnitten, so verhalten sich die Abschnitte auf den Parallelen wie die von Z ausgehenden entsprechenden Abschnitte auf der einen oder anderen Geraden

         a : a´ =  c : c´

         b : b´ =  c : c´

Begründungen mit Hilfe der zentrischen Streckung.

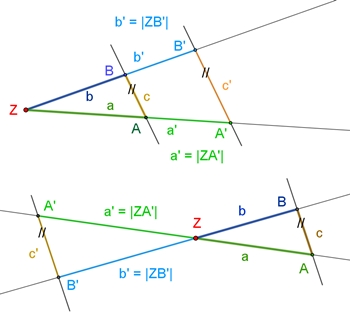
Ähnliche Figuren

Figuren F und G nennt man zueinander ähnlich, i. Z. F ∼ G, wenn man F durch eine zentrische Streckung so vergrößern oder verkleinern kann, dass das Bild F´ von F zu G kongruent ist.

Satz über ähnliche Figuren

Für ähnliche Figuren gilt:

I    entsprechende Strecken haben das gleiche Längenverhältnis,
II   entsprechende Winkel sind gleich groß,
III  sind die Seitenlängen der Figur k-mal so lang wie die von F, so ist der Flächeninhalt von G  k²-mal so groß wie der von F.

      Begründung mit Hilfe der zentrischen Streckung.

10)  Die Satzgruppe des Pythagoras

I  Der Satz des Pythagoras

Im rechtwinkligen Dreieck ist die Summe der Kathetenquadrate gleich dem Hypotenusenquadrat.

              a² + b²  =  c²

Begründungen s. Satz des Pythagoras

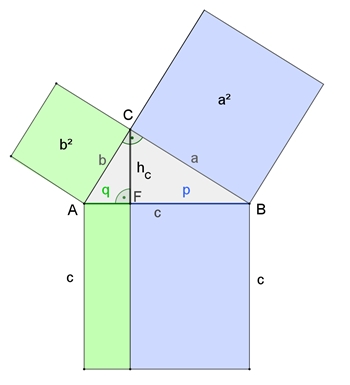
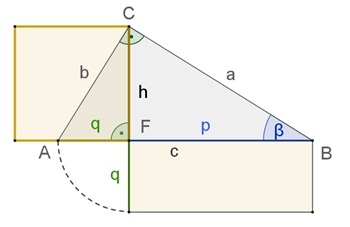
II  Der Kathetensatz

Beim rechtwinkligen Dreieck ist das Quadrat über einer Kathete flächengleich zum Rechteck aus der Hypotenuse und dem anliegenden Hypotenusenabschnitt.

          a² = p٠c,  b² = q٠c

Begründung:

Dreieck ABC ist ähnlich zu Dreieck BCF, da sie in zwei Winkeln (β und 90°) und damit in drei Winkeln (Winkelsumme im Dreieck) übereinstimmen. Daher gilt:
c : a = a : p  ⇔  a² = c٠p

III  Der Höhensatz

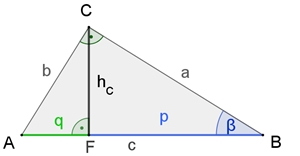
 Beim rechtwinkligen Dreieck ist das Quadrat über der Höhe flächengleich zum Rechteck aus den beiden Hypotenusenabschnitten.

                     h² = p٠q

Begründung:

Für das rechtwinklige Dreieck ABC mit 𝛾 = 90° gilt:
(1)  h² = b² – q² (Pythagoras im Dreieck AFD b² = h² + q²)
(2)  b² = c٠q  = (q + p)٠q

Einsetzen von (2) in (1) ergibt
h² = (q + p)٠q – q² = q² + p٠q – q² =  p٠q

11)  Sinus- und Kosinussatz

Festlegungen:

Mit γ = 90° gilt:

sin(α) = Gegenkathete : Hypotenuse

cos(α) = Ankathete : Hypotenuse

tan(α) = sin(α)/ cos(α) = Gegenkathete : Ankathete

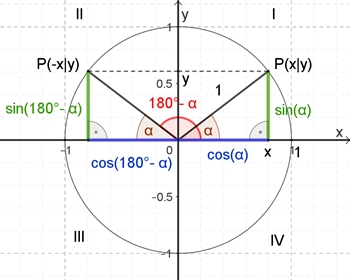
Am Einheitskreis gilt für den Punkt P(x|y):

x = cos(α), y = sin(α)

Quadrant I:     sin(α) > 0  und  cos(α) > 0
Quadrant II:    sin(α) > 0  und  cos(α) < 0
Quadrant III:   sin(α) < 0  und  cos(α) < 0
Quadrant IV:   sin(α) < 0  und  cos(α) > 0

sin(0°) = sin(180°) = 0,   cos(90°) = cos(270°) = 0
sin(90°) = 1;  sin(270°) = –1;  cos(0°) = 1;  cos(180°) = –1

Es gilt:  (sin(α))² + (cos(α))² = 1,  kurz:  sin²(α) + cos²(α) = 1 (Pythagoras)
              sin(180°– α) = sin(α);  cos(180°– α) = – cos(α)

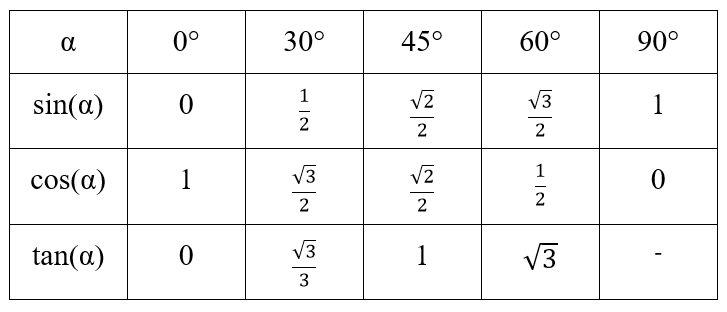
Tabelle besonderer Winkel

Sinussatz

Im Dreieck ABC verhalten sich die Längen zweier Seiten wie die Sinuswerte ihrer Gegenwinkel.
a : b  =  sin(α) : sin(β)
b : c  =  sin(β) : sin(γ)
a : c  =  sin(α) : sin(γ)

Begründung:

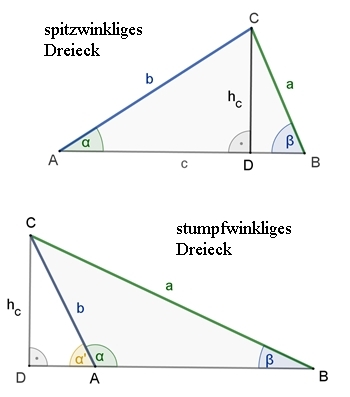
Im Δ ADC und Δ DBC gilt:
h_c = b٠sin(α)  und  h_c = a٠sin(β)

Im Δ DAC und Δ DBC gilt:
h_c = b٠sin(α´)  und  h_c = a٠sin(β),
wobei sin(α´)  = sin(180°– α) = sin(α)

Dann gilt in beiden Fällen
b٠sin(α)  =  a٠sin(β)  oder
a : b  =  sin(α) : sin(β) 

Entsprechende Begründungen für b : c  und  a : c

Kosinussatz

Im Dreieck ABC gilt:

a² = b² + c² – 2bc٠cos(α)
b² = a² + c² – 2ac٠cos(β)
c² = a² + b² – 2ab٠cos(γ)

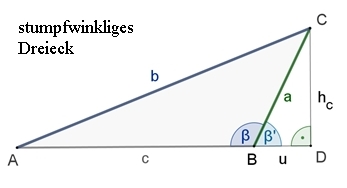
Begründungen:

(1)  s = a٠cos(β)  und  (2)  h_c = a٠sin(β)  (Δ DBC)
(3)  b² = (c – s)² + h_c²  (Pythagoras im Δ ADC)
Einsetzen von (1) und (2) in (3):
b² = (c – a٠cos(β))² + a²٠ sin²(β) 
b² = c² – 2ac٠cos(β) + a²٠cos²(β) + a²٠ sin²(β)
b² = c² – 2ac٠cos(β) + a²٠(cos²(β)  + sin²(β))
b² = c² – 2ac٠cos(β) + a²٠1

b² = a² + c² – 2ac٠cos(β)

(1)  u = a٠cos(β‘)  und  (2)  h_c = a٠sin(β‘)  (Δ DBC)
(3)  b² = (c + u)² + h_c²  (Pythagoras im Δ ADC)
Einsetzen von (1) und (2) in (3):
b² = (c + a٠cos(β‘))² + a²٠sin²( β‘)
b² = c² + 2ac٠cos(β‘) + a²٠cos²(β‘) + a²٠ sin²(β‘)
b² = c² + 2ac٠cos(β‘) + a²٠(cos²( β‘) + sin²( β‘))
b² = c² + 2ac٠cos(180°– β) + a²٠1, da β´ = 180°– β
b² = a² + c² – 2ac٠cos(β),  da cos(β) = – cos(180°–β)

Entsprechende Begründungen für die Gleichungen mit α und γ.