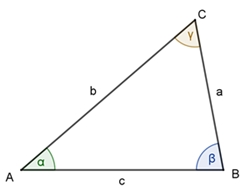
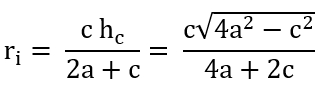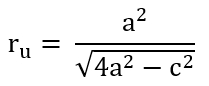DreieckeEinteilung von Dreiecken nach Winkeln
Im
spitzwinkligen Dreieck sind alle Winkel kleiner als 90°.
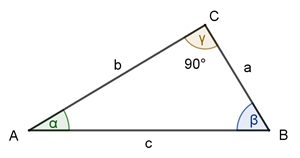
Im rechtwinkligen Dreieck ist ein Winkel
gleich 90°, z.B. γ = 90°.
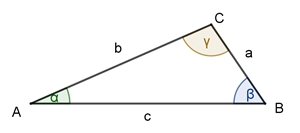
Im stumpfwinkligen Dreieck ist ein Winkel
größer als 90°.
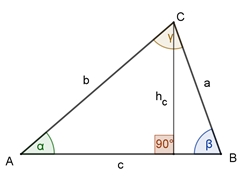
Flächeninhalt A des Dreiecks
A = ½
*
Grundlinie
*
Höhe
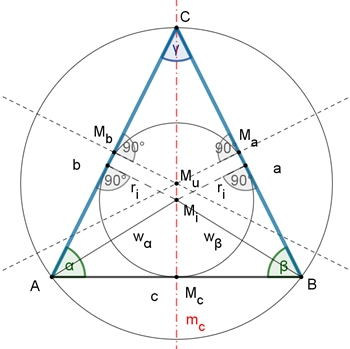
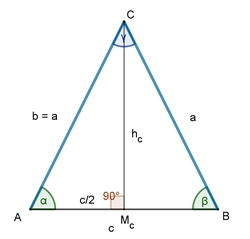
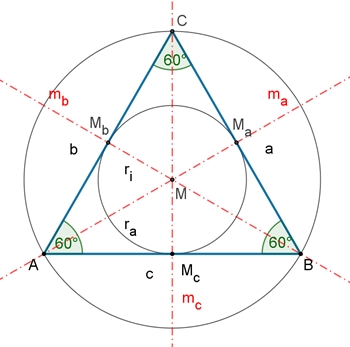
Das gleichschenklige Dreieck
Im gleichschenkligen Dreieck sind zwei Seiten gleich lang,
z.B. a = b
Dann gilt:
I Die
beiden Basiswinkel sind gleich groß, α = β falls a = b.
II Es besitzt
eine Symmetrieachse mc durch Mc und C, falls a = b.
III
Inkreis- und Umkreismittelpunkt befinden sich auf der Symmetrieachse.
Flächeninhalt A des
gleichschenkligen Dreiecks
hc2 + (c/2)2
= a2 (Pythagoras im Dreieck AMcC)
Daraus folgt:
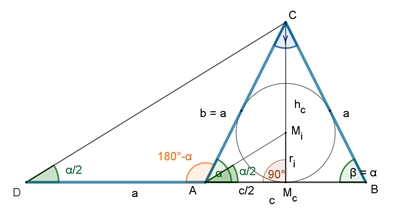
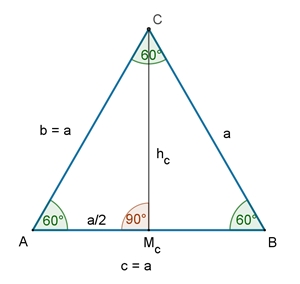
Inkreisradius
des
gleichschenkligen Dreiecks
Bei gegebenem a und c:
ri : c/2 = hc : (a +
c/2) (Dreieck AMcC
ist ähnlich zu Dreieck DMcC)
Bei gegebenem c
und
α
ri / c/2 = tan(α/2)
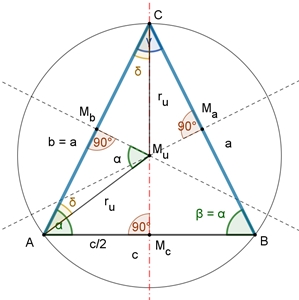
Umkreisradius des gleichschenkligen Dreiecks
Bei gegebenem a und c:
ru : a/2 = a : hc
(Dreieck MuMbA ist ähnlich zu Dreieck AMcC) ;
Bei gegebenem c und
α:
sin(α) = a/2 / ru
(Sinus im Dreieck MuMbA)
Das gleichseitige Dreieck
Im gleichseitigen Dreieck sind alle Seiten gleich lang,
a = b = c.
Dann gilt:
I Alle
Winkel sind gleich groß, α = β = γ =
60°.
II Es besitzt
drei Symmetrieachsen durch den Mittelpunkt und hat eine 3-fache
Rotationssymmetrie.
III
Inkreis und Umkreis besitzen den
gleichen Mittelpunkt M.
Flächeninhalt A des
gleichseitigen Dreiecks
hc2 + (a/2)2 = a2 (Pythagoras im Dreieck AMcC)
Daraus folgt:
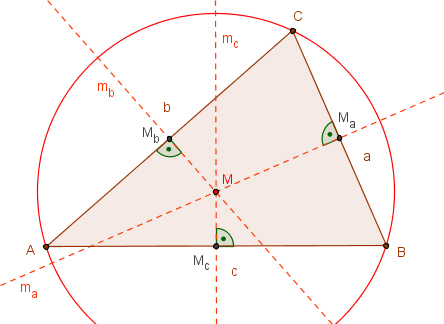
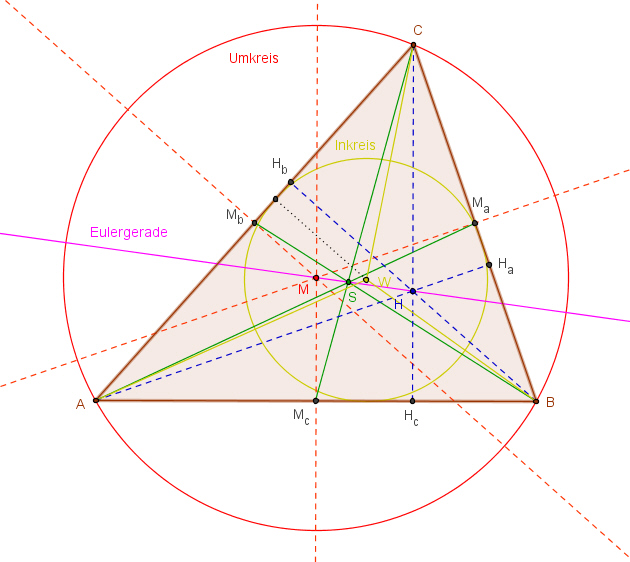
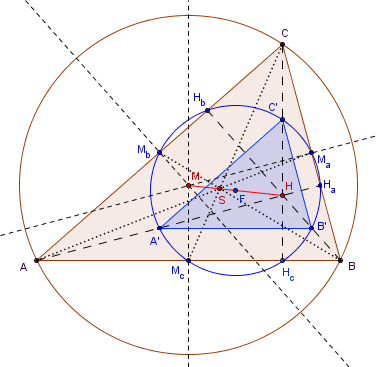
Bestimmungsstücke im Dreieck1. Die drei Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt M, dem Mittelpunkt des Umkreises des Dreiecks.
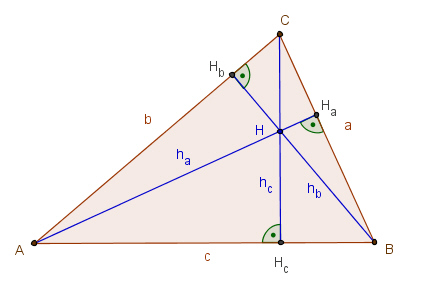
2. Die drei Höhen eines Dreiecks schneiden sich in einem Punkt H.
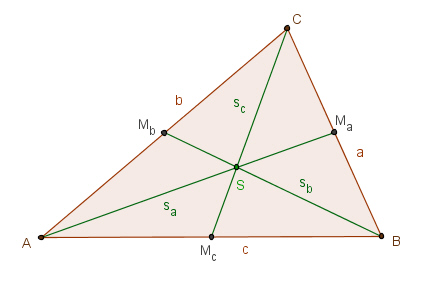
3. Die drei
Seitenhalbierenden schneiden sich in einem Punkt S, dem
Schwerpunkt des Dreiecks.
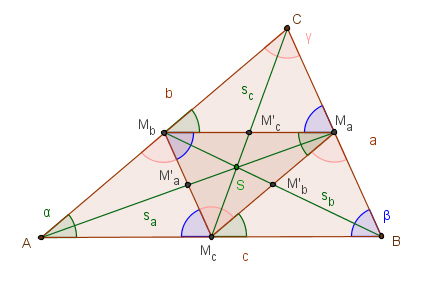
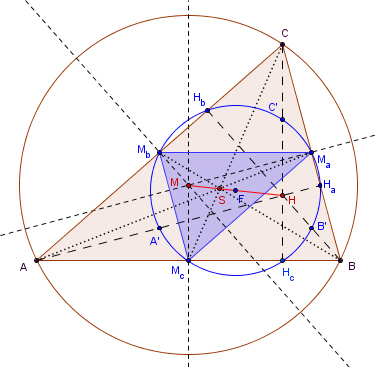
Eigenschaften des Mittendreiecks MaMbMc:
c) Die zentrische Streckung mit Zentrum S und
Streckungsfaktor -0,5 bildet das Dreieck
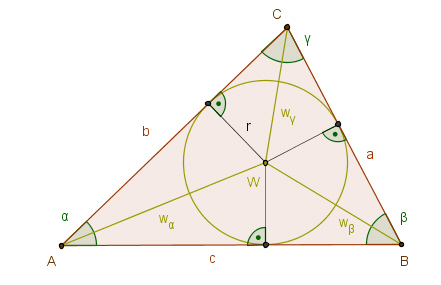
4. Die drei Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt W, dem Inkreismittelpunkt des Dreiecks.
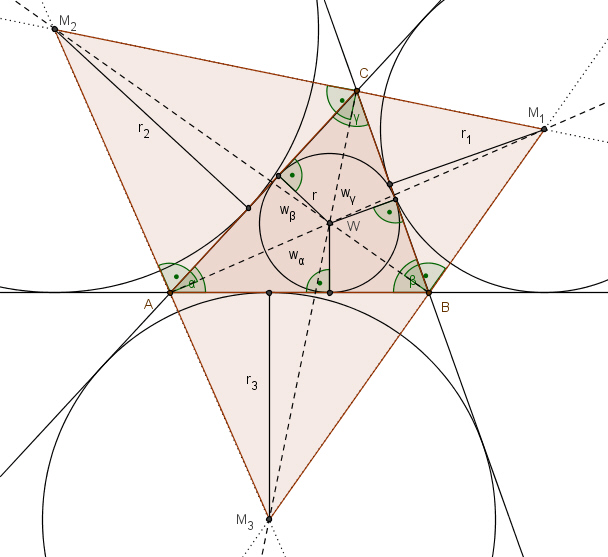
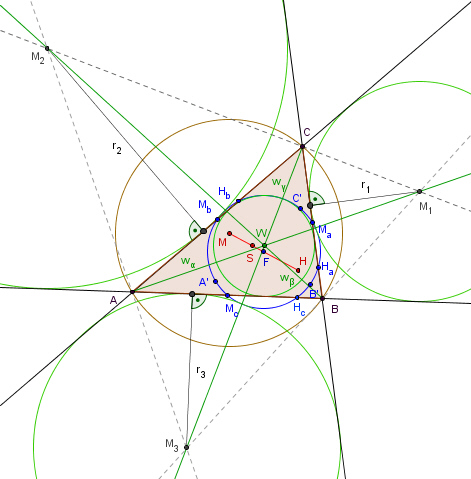
Eigenschaft des Dreiecks M1M2M3,
wobei M1, M2, M3 die Mittelpunkte der Ankreise des Dreiecks ABC sind:
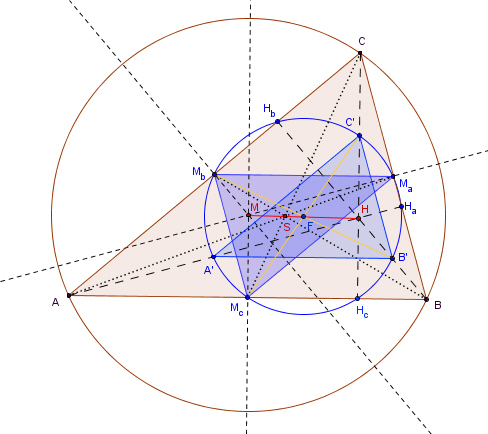
Die
Euler-Gerade und der Feuerbachkreis.
Die Euler-Gerade im Dreieck:
Satz über die Euler-Gerade: In jedem Dreieck
liegt der Schnittpunkt H der
Höhen, der
Schnittpunkt S der Seitenhalbierenden, der Mittelpunkt des
Feuerbachkreises F
und der Schnittpunkt M der Mittelsenkrechten liegen auf einer Geraden. Diese
Gerade heißt Euler-Gerade. Satz über den Feuerbachkreis:
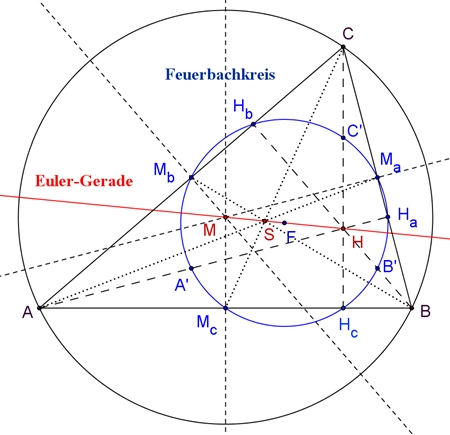
Die
Seitenmitten Ma, Mb, Mc und die Höhenfußpunkte
Ha, Hb, Hc eines Dreiecks und die Mittelpunkte
A’, B’, C’ zwischen den Dreiecksecken und dem Höhenschnittpunkt liegen
auf einem Kreis. Dieser Kreis heißt Feuerbachkreis oder
Neunpunktekreis.
Weitere Eigenschaften: 1. Die Euler-Gerade geht auch durch den Mittelpunkt F des Feuerbachkreises; der Mittelpunkt dieses Kreises ist gleichzeitig der Mittelpunkt der Strecke [HM]. 2. Die vier Punkte M, S, F und H sind vier harmonische Punkte mit dem Teilverhältnis | τ | = 2 : 1.
3. Im
Dreieck ABC
besitzt
der
Feuerbachkreis einen
halb so
großen Radius wie der Umkreis des Dreiecks. 4. Die zentrische Streckung (H; 0,5) mit Zentrum H und Streckungsfaktor 0,5 bildet das Dreieck ABC auf das Dreieck A’B’C’ und den Umkreis des Dreiecks ABC auf den Feuerbachkreis ab.
5. Die zentrische Streckung (S; -0,5) mit Zentrum S und Streckungsfaktor -0,5 bildet das Dreieck ABC auf das Dreieck MaMbMc und den Umkreis des Dreiecks ABC auf den Feuerbachkreis ab.
6. Die beiden zentrischen Streckungen (S;
-0,5)
und (H; 0,5) hängen folgendermaßen zusammen: 7. Beim gleichseitigen Dreieck wird der Neunpunktekreis zum Inkreis des Dreiecks. 8. Der Neunpunktekreis wird vom Inkreis und von den drei Ankreisen des Dreiecks ABC berührt.
Mandala aus gleichschenkligen Dreiecken bestehend
Konstruktion nach einem Mosaik in einer
römischen Villa aus dem 1. Jhd. n. Chr.
Sämtliche Konstruktionen wurden mit Hilfe von geogebra durchgeführt. Quelle für Beweise: http://lsgm.uni-leipzig.de/KoSemNet/pdf/graebe-99-1.pdf
|