Die Friesgruppe oder Bandornamentgruppe

Unter einem Bandornament oder Fries versteht man in der Mathematik ein Streifenmuster, bei dem man kleinste Einheiten (Zellen, Muster) entlang einer bestimmten Richtung (Friesrichtung oder Richtung der Verschiebung) immer wieder aneinandersetzt, wobei das Bandornament keinen Anfang und kein Ende besitzt. Das Fries kann nach ihren Symmetrieeigenschaften in 7 Typen eingeteilt werden, die die Friesgruppe bilden.

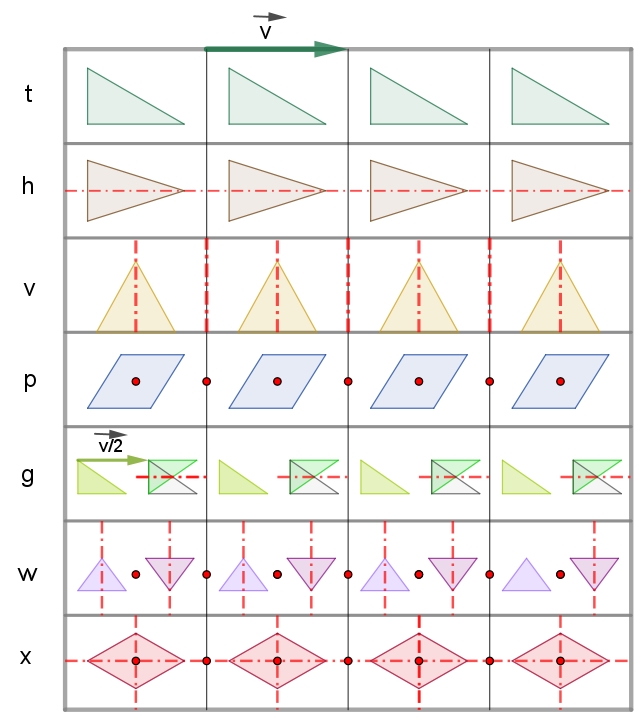
Bezeichnungen:

t  = Translation (Verschiebung) mit dem Vektor k٠ , k ganze Zahl, für k=0 identische Abbildung (p1)

h = horizontale Spiegelung und Translation (p11m)

v = vertikale Spiegelung und Translation (p1m1)

p = Punktspiegelung und Translation (p2)

g = Gleitspiegelung und Translation (p11g)

w = Punktspiegelung, Gleitspiegelung und Translation (p2mg)

x = horizontale, vertikale Spiegelung, Punktspiegelung, Gleitspiegelung und Translation (p2mm)

Die übliche Klassifizierung steht in Klammern

Die 7 Friesgruppen:

Die Abbildungen h, v und p bilden jeweils eine Untergruppe, die der zyklischen Gruppe C2 entspricht (zu C2 isomorph ist).

Die Abbildungen t, h, v und p bilden zusammen eine Untergruppe, die zur Diedergruppe D2 isomorph ist.

Die Abbildung w ist zusammengesetzt aus p, g und t.

Die Abbildung x ist zusammengesetzt aus h, v, p, g und t

Die sieben verschiedenen Gruppen entsprechen den 7 unendlichen Reihen axialer Punktgruppen in drei Dimensionen.

Beispiele von Bandornamenten mit Kennzeichnung der Zelle (Muster) und der Abbildung

  h

  v

  p 

 

 
 
 
  x
 
 
 

 

 
 
  v

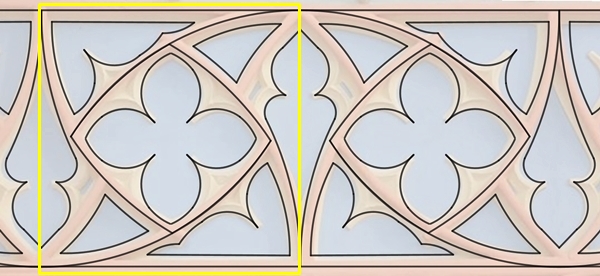Die Fotos der Bandornamente wurden in Andalusien, Marokko und Usbekistan aufgenommen.