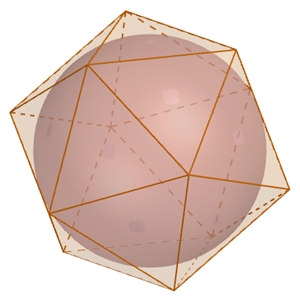
Das Ikosaeder

Das Ikosaeder besitzt als Oberfläche 20 kongruente gleichseitige Dreiecke, 30 gleich lange Kanten und 12 Ecken.
Die Kantenlänge sei a.

Berechnung des Umkugelradius des Ikosaeders: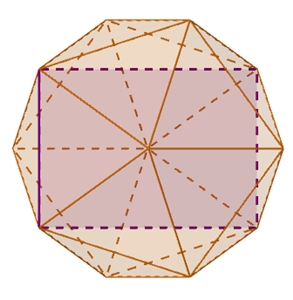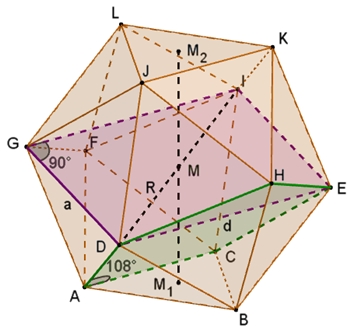

Aus Symmetriegründen ist DEIG ein Rechteck im Ikosaeder, und zwar ein goldenes Rechteck mit den Seiten a und d, wobei gilt:
     (siehe goldener Schnitt, Konstruktionen)

d ist Diagonale im regulären Fünfeck ACEHD.

Der Umkugelradius R ist die halbe Diagonallänge des goldenen Rechtecks:
(2R)² = a² + d²  (Pythagoras)

4 R² = a² + a²/2⸱(3 + √5)
R² = a²/8⸱(5 + √5)

R = a/4⸱√(10 + 2√5)

Umkugelradius R des Ikosaeders:

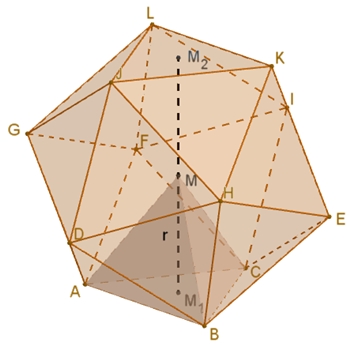
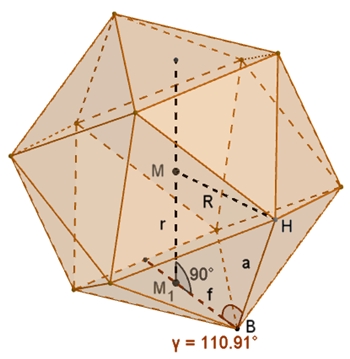
Berechnung des Inkugelradius des Ikosaeders: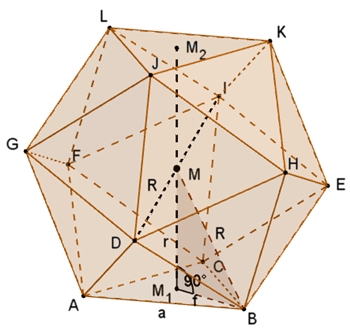

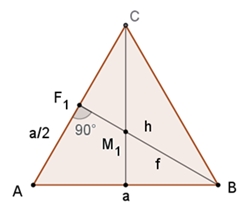
h = a/2 √3 (Pythagoras im Dreieck ABF₁)

f = 2/3 h = a/3 √3 (M₁ teilt die Höhe im Verhältnis 2 : 1)

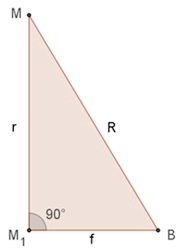
r² = R² – f²  (Pythagoras im Dreieck M₁BM)
r² = a²/8⸱(5 + √5) – a²/3
r² =  a²/24⸱(7 + 3√5)

Inkugelradius r des Ikosaeders:  r = 1/12⸱(√15 + 3√3) a ≈ 0,756 a

Ikosaeder mit Inkugel und Umkugel

Berechnung des Oberflächeninhalts des Ikosaeders:

Der Oberflächeninhalt eines Ikosaeders ist der 20-fache Flächeninhalt eines gleichseitigen Dreiecks.

Flächeninhalt des gleichseitigen Dreiecks: A = 1/2 a h = a²/4 √3

Oberflächeninhalt O des Ikosaeders mit O = 20 A: 

O = 5√3 a² ≈ 8,660 a²

Berechnung des Volumeninhalts des Ikosaeders:

Der Volumeninhalt eines Ikosaeders ist der 20-fache Volumeninhalt einer Pyramide aus dem gleichseitigen Dreieck mit Spitze M.

Volumeninhalt der Pyramide ABCM:

V₃ = 1/3 A r = a²/12 √3⸱1/12⸱(√15 + 3√3) a
V₃ = a³/144⸱(9 + 3√5)
V₃ = a³/48⸱(3 + √5)

Volumeninhalt V des Ikosaeders mit V = 20 V₃:  

V = 5/12 (3 + √5) a³ ≈ 2,182 a³

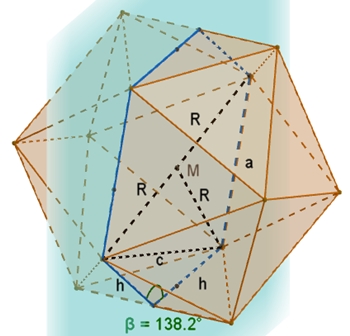
Berechnung der Winkel im Ikosaeder

Der Innenwinkel α des gleichseitigen Dreieck α = 60° (= 180°/3).

Berechnung des Winkels β zwischen benachbarten Flächen:

c² = (2R)² – a²  = 1/2 (5 + √5) a² – a²
c² = 1/2 (3 + √5) a²

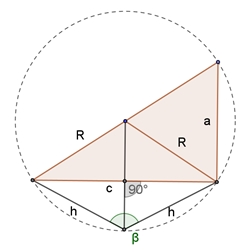
c = (1 + √5)/2 a

sin(β/2) = ((1 + √5)/4 a) / (1/2 √3 a)

sin(β/2) = 1/6⸱(√3 + √15)

β = 180° – arcsin(2/3) ≈ 138,190°

Winkel β zwischen benachbarten Flächen:  β = 180° – arcsin(2/3) ≈ 138,190°

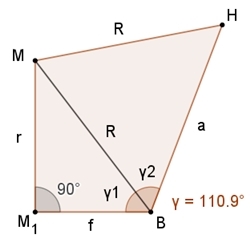
Berechnung des Winkels γ zwischen Kante und Fläche:

tan(γ1) = r / f = (1/12⸱(√15 + 3√3) a) / (√3/3 a)

tan(γ1) = 1/4⸱(3 + √5)
γ1 = arccot(3 – √5) ≈ 52,623°

R² = a² + R² – 2aR cos(γ2)   (Kosinussatz)

2aR cos(γ2) = a²

cos(γ2) = a / (2R)

cos(γ2) = 2 / √(10 + 2√5)

γ2 = arccos(2 / √(10 + 2√5))       

γ2 = 1/2 (135 – arctan(1/3))

γ = γ1 + γ2 = arccot(3 – √5) + 1/2 (135 – arctan(1/3))

γ = 1/4⸱(450° – arcsin(1/9)) ≈ 110,905° 

Winkel γ zwischen Kante und Fläche:  γ = 1/4⸱(450° – arcsin(1/9)) ≈ 110,905° 

Zurück

Zurück zur Themenseite
Zurück zur Startseite