Zylinder, Kugel und Kegel

Volumen- und Oberflächeninhalt von geradem Zylinder, Kugel und geradem Kreiskegel

           V_Z = r²π h                                V_Ku = 4/3 r³π                        V_Ke = 1/3 r²π h

           O_Ku =  2r²π + 2rπh                   O_Ku = 4r²π                            O_Ke = r²π + rsπ

          r = Radius, h = Höhe, s = Mantellinie des Kegels 

          Herleitungen: Ebene und räumliche Geometrie
 

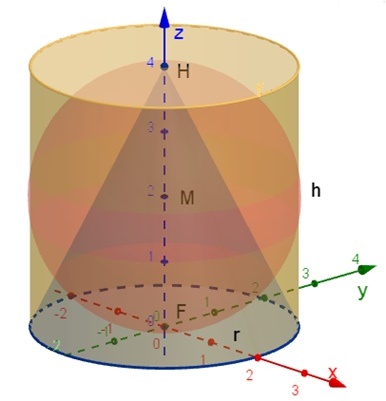
Zylinder mit einbeschriebener Kugel und einbeschriebenem Kegel

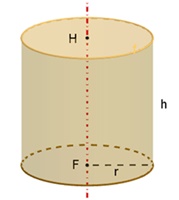
Gegeben ist ein gerader Zylinder mit der Höhe h und einer Kreisfläche mit Radius r = h/2 als Grundfläche.

Volumeninhalte:

Zylindervolumen V_Z = r²π h = 2 r³π

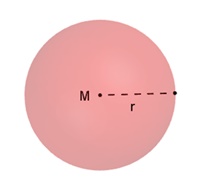
Dem Zylinder wird eine Kugel mit Radius r einbeschrieben:

Kugelvolumen V_Ku = 4/3 r³π

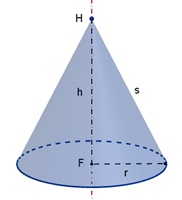
Dem Zylinder wird ein gerader Kreiskegel mit Radius r und Höhe h = 2r einbeschrieben:

Kegelvolumen V_Ke = 1/3 r²π h = 2/3 r³π

Damit gilt für das Verhältnis der Volumeninhalte:

V_Ke : V_Ku : V_Z = 2/3 r³π  :  4/3 r³π  :  6/3 r³π = 2 : 4 : 6

V_Ke : V_Ku : V_Z =  1 : 2 : 3

Oberflächeninhalte:

Zylinderoberfläche O_Ku =  2r²π + 2rπh = 6r²π

Kugeloberfläche O_Ku = 4r²π

Kegeloberfläche O_Ke = r²π + rsπ = r²π (1 + )    NR: s² = r² + (2r)² = 5r²  (Pythagoras)

Damit gilt für das Verhältnis der Oberflächeninhalte:

O_Ke : O_Ku : O_Z  =  r²π (1 + )  :  4r²π  :  6r²π  = (1 + )  :  4  :  6

Speziell gilt:

V_Ku : V_Z =  O_Ku : O_Z  =  2 : 3

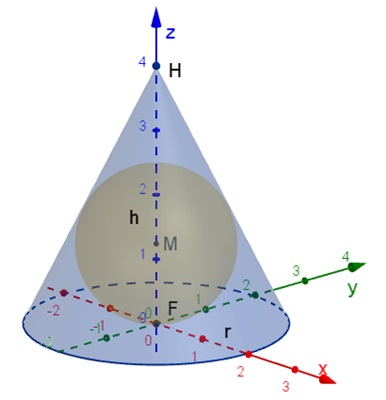
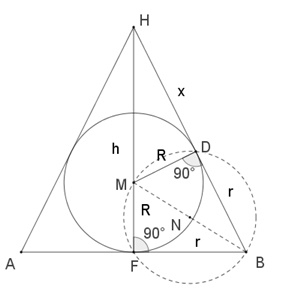
Gerader Kreiskegel mit einbeschriebener Kugel

Kegel der Höhe h = 2r mit Radius r des Grundkreises mit einbeschriebener Kugel mit Radius R.

Senkrechter Schnitt zur xy-Ebene durch F, N ist Mittelpunkt von [MB]:

NR:

x : R  =  h : r   (ähnliche Dreiecke MDH und FBH)

Mit h = 2r folgt:  x = 2R

(2R + r)² = (2r)² + r²   (Pythagoras im Dreieck FBH)

2R + r = r

 (σ = goldene Schnittzahl ≈ 0,618)

Kegelvolumen V_Ke = 1/3 r²π h = 2/3 r³π

Kugelvolumen V_Ku = 4/3 R³π = 4/3 ( – 2) r³π

Verhältnis der Volumeninhalte:

V_Ke : V_Ku  =  2/3 r³π  :  (4/3 ( – 2) r³π)  =  /2 + 1 =  ( + 1)/2 + 1/2

V_Ke : V_Ku =  τ + 0,5  ≈  2,118   (τ = goldene Schnittzahl ≈ 1,618)

Verhältnis der Oberflächeninhalte:

Kugeloberfläche O_Ku = 4 R²π = 4 r²π = 2 (3 – ) r²π

Kegeloberfläche O_Ke = r²π + rsπ = r²π + r (r + 2R) π = r²π + r²π = (1 + ) r²π

O_Ke : O_Ku  = (1 + ) r²π  :  2 (3 – ) r²π  =  / 2 + 1 = ( + 1)/2 + 1/2

O_Ke : O_Ku  =  τ + 0,5  ≈  2,118  

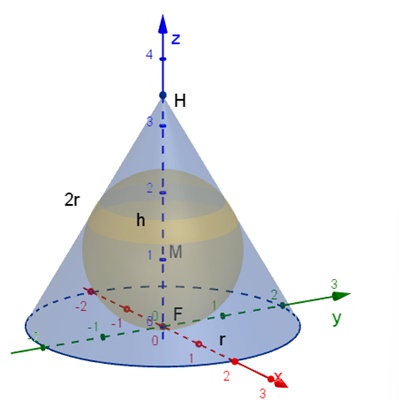
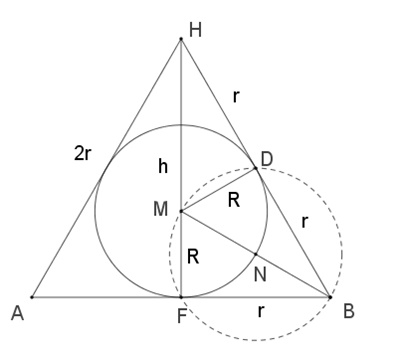
Kegel mit Mantellinie 2r und Radius r des Grundkreises und mit einbeschriebener Kugel mit Radius R.

Senkrechter Schnitt zur xy-Ebene durch F, N ist Mittelpunkt von [MB]:

NR:

h² = (2r)² – r²  (Pythagoras im Dreieck FBH)

h = r

R : r = r : h  (ähnliche Dreiecke FBM und FBH)

R = r /

Kegelvolumen V_Ke = 1/3 r²π h = /3 r³π

Kugelvolumen V_Ku = 4/3 R³π = 4 / (9) r³π 

Verhältnis der Volumeninhalte:

V_Ke : V_Ku =  /3 r³π  :  (4 / (9) r³π)  =

V_Ke : V_Ku =  2,25

Verhältnis der Oberflächeninhalte:

Kugeloberfläche O_Ku = 4R²π = 4/3 r²π

Kegeloberfläche O_Ke = r²π + rsπ = 3 r²π, wobei s = 2r

O_Ke : O_Ku  =  2,25

Zurück
Zurück zur Startseite