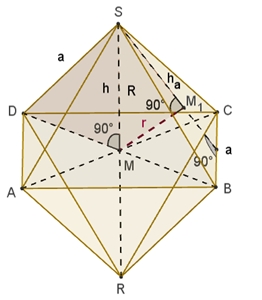
Das Oktaeder

Das Oktaeder besitzt als Oberfläche 8 kongruente gleichseitige Dreiecke, 12 gleich lange Kanten und 6 Eckpunkte.
ABCD ist wegen der Achsensymmetrie mit Achse RS ein Quadrat. Die Kantenlänge sei a.

Oktaeder-1

 

Berechnung des Um- und Inkugelradius des Oktaeders:

Für die Länge d der Diagonale des Quadrats ABCD gilt:
d² = a² + a² (Pythagoras)

d = √2 a

Für die Höhe h gilt nach Pythagoras:
h2 + (1/2 √2 a)2 = a2 

h = 1/2 √2 a = 1/2 d

Damit ist der Umkugelradius R = 1/2 √2 a ≈ 0,707 a

Für den Inkugelradius gilt:

r² + (2/3 ha)² = h²

r² = 1/2 a² – (2/3⸱ a/2 √3)² ;  r² = 1/6 a²  

Damit ist der Inkugelradius r = 1/6 √6 a ≈ 0,408 a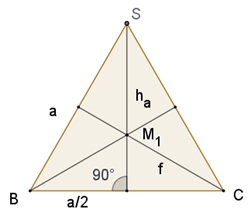

 
okta-dreieck 

NR:

a² = (a/2)² + ha²
ha = 1/2 √3 a
M1 teilt die Höhe im Verhältnis 2 : 1.
M1 ist Mittelpunkt einer gleichseitigen Pyramide mit Grundfläche BCS und Spitze M. Damit steht r = |MM1| senkrecht auf M1S.

 

In- und Umkugel des Oktaeders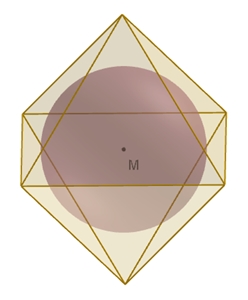

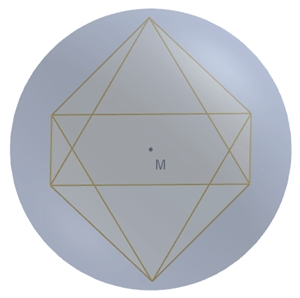
Inkugel            Umkugel

Berechnung des Oberflächen- und Volumeninhalts des Oktaeders:

Der Oberflächeninhalt eines Dodekaeders ist der 8-fache Flächeninhalt eines gleichseitigen Dreiecks mit dem Flächeninhalt A.
A = 1/2 a ha = 1/4 √3 a²
 Für den Oberflächeninhalt des Oktaeders gilt dann:
O = 8 A = 2 √3 a² ≈ 3,464 a²

Für den Volumeninhalt V gilt:
Volumeninhalt der Pyramide ABCDS: V = 1/3 a² h = 1/3 a²⸱ 1/2 √2 a = 1/6 √2 a³

Damit ist der Volumeninhalt des Oktaeders V = 1/3 √2 a³ ≈ 0,471 a³

Berechnung der Winkel im Oktaeder:

Innenwinkel α des gleichseitigen Dreiecks α = 60° (= 180°/3).

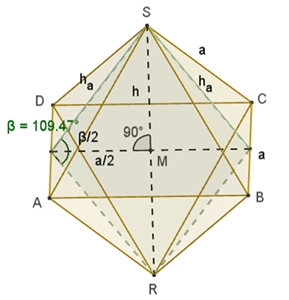
Oktaeder-2

 

  

  

Berechnung des Winkels β zwischen benachbarten Flächen des Oktaeders:

tan(β/2) = h / a/2

tan(β/2) = √2

β/2 = arctan(√2) = 54,736°

Der Winkel β zwischen benachbarten Flächen eines Oktaeders beträgt β = 109,471°.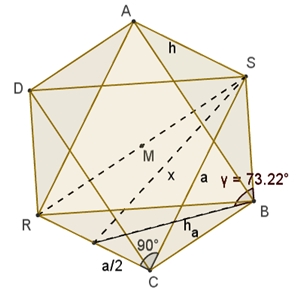

 
 
 
 
 
Oktaeder-3
 
Berechnung des Winkels γ zwischen Kante und Fläche eines Oktaeders:

Das Dreieck RCS ist gleichschenklig rechtwinklig mit |RS| = √2 a. Damit gilt:
x² = a² + (a/2)²  (Pythagoras)
x = 1/2 √5 a 

x² = a² + ha² – 2a ha cos(γ)  (Kosinussatz)
5/4 a²  = a² + 3/4 a²  –  √3 a² cos(γ)

√3 cos(γ) = 1/2

cos(γ) = 1 / 2√3

γ = 73,221°

Der Winkels γ zwischen Kante und Fläche des Oktaeders beträgt γ = 73,221°.


 

Zurück

Zurück zur Themenseite
Zurück zur Startseite