Der Würfel (das Hexaeder)

Der Würfel ist einer der 5 platonischen Körper mit folgenden Eigenschaften:

Er besteht aus 6 kongruenten Quadraten (f).
Er besitzt 12 gleich lange Kanten (k).
Er hat 8 Eckpunkte (e).

Es gilt der Polyedersatz von Euler: e + f = k + 2

Volumeninhalt V eines Würfels mit der Kantenlänge a:  V = a³

Oberflächeninhalt O eines Würfels mit der Kantenlänge a:  O = 6 a²

Netz des Würfels
Im Würfel gegenüberliegende Quadrate sind mit gleicher Farbe gekennzeichnet.

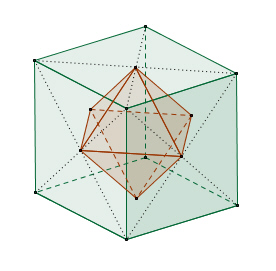
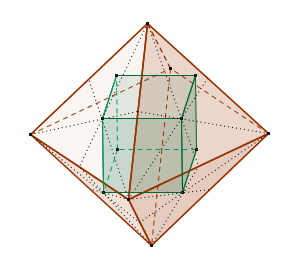
Würfel und Oktaeder sind zwei Dualkörper.

Wenn man die Mittelpunkte zweier benachbarter Seitenflächen eines platonischen Körpers verbindet, erhält man wieder einen platonischen Körper mit demselben Mittelpunkt.
Der Dualkörper zum Würfel ist das Oktaeder und umgekehrt ist der Würfel der Dualkörper zum Oktaeder. Dabei wird die Anzahl der Flächen mit der Anzahl der Ecken vertauscht, während die Anzahl der Kanten gleich bleibt.

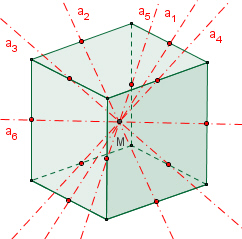
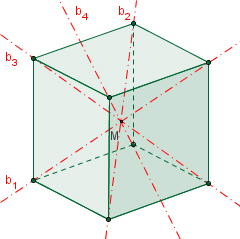
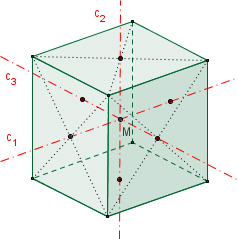
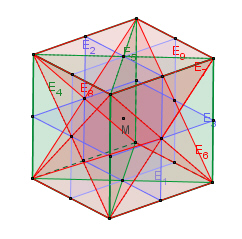
Symmetrie des Würfels

Der Würfel besitzt 6 zweizählige Drehachsen a durch die Mittelpunkte gegenüberliegender Kanten,
4 dreizählige Drehachsen b durch gegenüberliegende Ecken,
3 vierzählige Drehachsen c durch die Mittelpunkte gegenüberliegender Flächen,
9 Symmetrieebenen E, jeweils drei Ebenen durch je vier Ecken, sechs Ebenen durch jeweils zwei Ecken und zwei Kantenmittelpunkte,1 Punktsymmetrie zum Mittelpunkt.

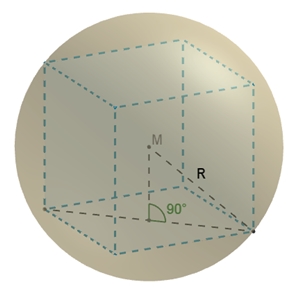
Umkugel des Würfels

Berechnung des Radius R der Umkugel:

R² = (a/2)² + (a√2/2)²  (Pythagoras)

R = a√3 /2

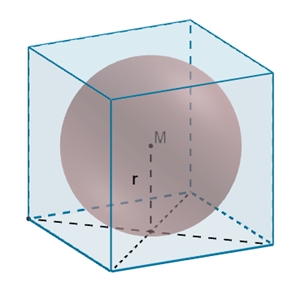
Inkugel des Würfels

Radius r der Inkugel:

r = a/2

Schnittflächen des Würfels

Gleichseitiges Dreieck, reguläres Sechseck und Rechteck mit Raute im Würfel

Anzahl der Würfel in einem Würfel, der aus n³ gleich großen kleinen Würfeln zusammengesetzt ist.

Der kleine Würfel kommt im großen Würfel 4٠4٠4 = 4³ Mal vor.
Der grüne Würfel – aus 2³ = 8 kleinen Würfeln bestehend – kommt im großen Würfel 3٠3٠3 = 3³ Mal vor.
Der braune Würfel – aus 3³ = 27 kleinen Würfeln bestehend – kommt im großen Würfel 2٠2٠2 = 2³ Mal vor.

Es gibt insgesamt 1 + 2³ + 3³ + 4³ = 100 Würfel.

Bei einem Würfel, der aus n³ gleich großen kleinen Würfeln zusammengesetzt ist, gibt es mit dem Würfel selbst insgesamt

1 + 2³ + 3³ + … +  n³ = n²٠(n + 1)² / 4  Würfel.

Zurück

Zurück zu Themen
Zurück zur Startseite