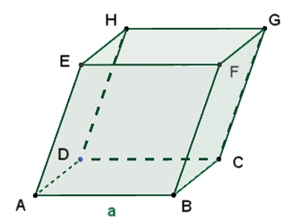
Das Rhomboeder

Das Rhomboeder ist ein Polyeder, das von sechs kongruenten Rauten begrenzt wird.

Raute mit der Seitenlänge a den Diagonallängen e und f und den Winkeln α und β.

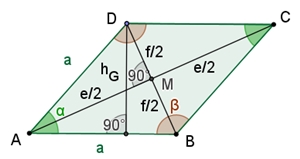
Berechnung des Flächeninhalts A_R der Raute ABCD:

h_G / a = sin(α)
h_G = a sin(α)
A_R = a h_G = a² sin(α)

Berechnung von f und e in Abhängigkeit von a und α:

sin(β/2) = (h_G /2) / (f/2)

f = h_G / sin(90°– α/2)

f = a sin(α) / sin(90°– α/2)

f = 2 a sin(α/2)

sin(α/2) = (h_G /2) / (e/2)

e = h_G / sin(α/2)

e = a sin(α) / sin(α/2)

e = 2 a cos(α/2)

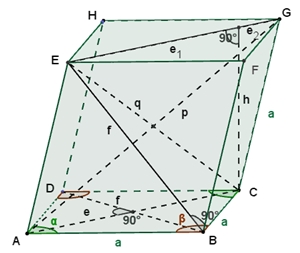
Berechnung von h mit Pythagoras und CAS:

h² + e₂² = a²

I   e₂ = √( a² – h²)

h² + e₁² = q²  und  q² = f² + a². Daraus folgt:

h² + e₁² = f² + a²  

II   e₁ = √f² + a² –  h²) 

sin(α/2) = f/2 / a  oder  f = 2a sin(α/2) oder f = 2a √(1 – cos(α))/2),  eingesetzt in II:

II‘  e₁ = √(4a² (1 – cos(α))/2 + a² –  h²) 

III  e = e₁ + e₂

cos(α/2) = e/2 / a   oder   e = 2a cos(α/2)    oder   e = 2a  √(1 + cos(α))/2) mit I und II‘ eingesetzt in III:

2a  √(1 + cos(α))/2)  =  √(4a² (1 – cos(α))/2 + a² –  h²)  + √( a² – h²)

Lösung mit Hilfe eines Computer-Algebra-Systems (CAS):

h = a tan(α/2) √(1 + 2 cos(α))

Volumeninhalt V des Rhomboeders:

V = A_R h

V = a³ sin(α) tan(α/2) √(1 + 2 cos(α))  oder

V = a³ √(1 – 3 cos²(α) + 2 cos³(α))

Berechnung der Länge der Raumdiagonalen p und q in Abhängigkeit von a und α:

q² = f² + a² und f = 2 a sin(α/2). Daraus folgt:

q² = 4 a² sin(α/2)² + a² = a² (1 + 4 sin(α/2)²)

q = a √((3 – cos(α))/2)

q = a √(3 – 2 cos(α)) (3 kurze Raumdiagonalen CE, BH und DF)

p² = (e + e₂)² + h²  (Pythagoras)

p² = (2a cos(α/2) + √( a² – h²) )² + h²  und  h = a tan(α/2) √(1 + 2 cos(α))

Ergebnis mit Hilfe von CAS

p = a √(3 – 6 cos(α)) (1 lange Raumdiagonale AG)

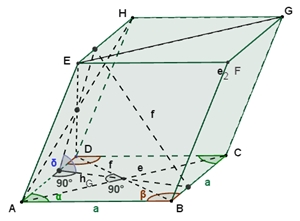
Winkel δ₁ und δ₂ zwischen benachbarten Flächen

f² = h_G² + h_G² – 2 h_G² cos(δ₁)  (Kosinussatz)

cos(δ₁)  = (2 h_G² – f²) / 2 h_G²

cos(δ₁)  = (2a² sin(α) ² – 4 a² sin(α/2) ²) / (2 a² sin(α)²)

cos(δ₁)  = 1 – (2 sin(α/2)²)/  sin(α)²

δ₁ = arccos(1 – (2 sin(α/2)²)/  sin(α)²)

δ₁ = arccos(cos(α)/(1 + cos(α))

δ₂ = 180° – δ₁ (gegenüberliegende Flächen sind parallel)

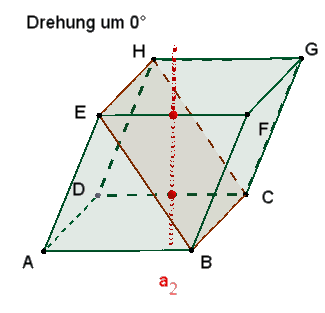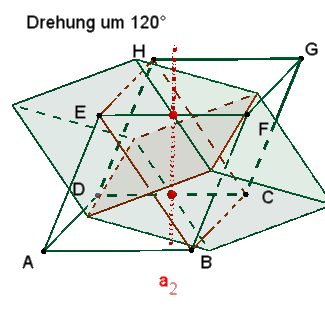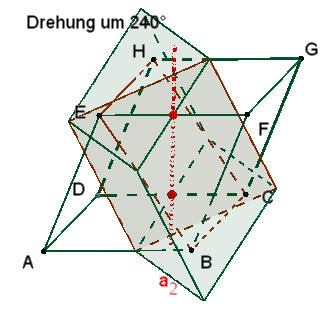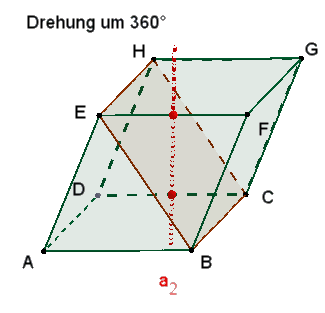
Rotationssymmetrien

2 zweizählige Drehachsen a₁ und a₂ durch die Mitten gegenüberliegender Seiten.

Das Viereck BCHE kommt nach einer 180°-Drehung um die Drehachsen a₁ auf sich zu liegen und muss deshalb ein Rechteck sein. (Begründung für  ≮ EBC = 90°)

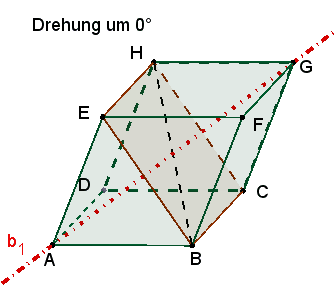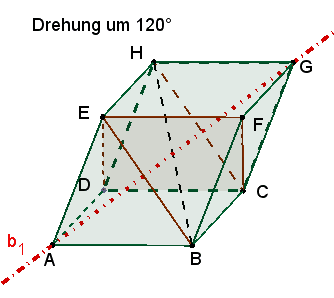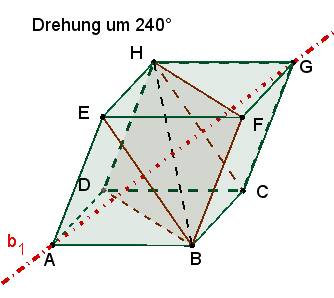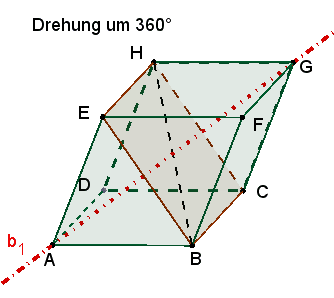
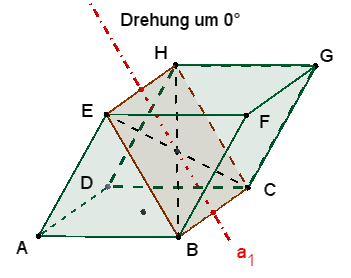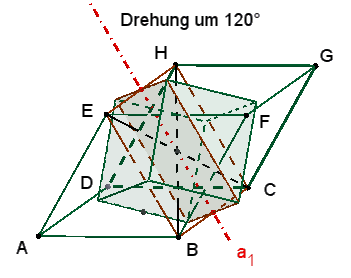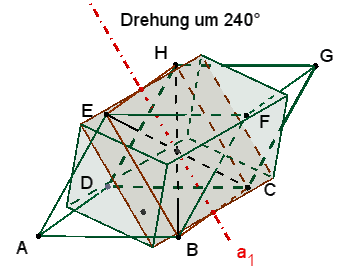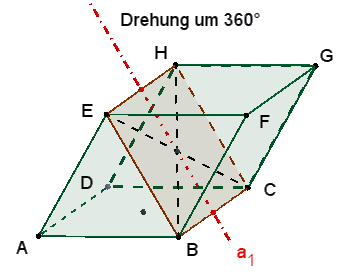
1 dreizählige Drehachse b₁ durch die Eckpunkte A und G.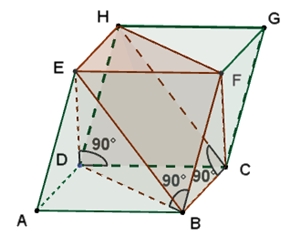

Die 3 kongruenten Rechtecke mit den Seiten a und f sind zu sehen nach einer Drehung um 120°, 240° und 360° ≙ 0°.

Zurück

Zurück zur Themenseite
Zurück zur Startseite