Das Tetraeder

Das Tetraeder besitzt als Oberfläche 4 kongruente gleichseitige Dreiecke, 6 gleich lange Kanten und 4 Eckpunkte.
Die Kantenlänge sei a.

Berechnung des In- und Umkugelradius r des Dodekaeders mit der Kantenlänge a:

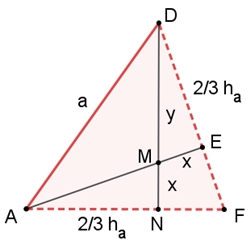
Höhe h_aim gleichseitigen Dreieck

h_a² + (a/2)² = a² (Pythagoras)

h_a = a/2 √3

N ist der Mittelpunkt des gleichseitigen Dreiecks und teilt h_a im Verhältnis 2 : 1.

Begründung:
Dreieck ABC an F punktgespiegelt liefert die Raute ABA’C.
Die Strecke NC wird zur punktgespiegelten Strecke N’B.
|BN‘| : |GN| = 2 : 1 (Strahlensatz).
Daraus folgt: |CN| : |NG| = 2 : 1.

Daraus folgt für die Höhe h des Tetraeders:

a² = h² + (2/3 h_a)²
h² = a² – (a/3 √3)²

h² = 2/3 a²,  h = 1/3 √6 a

Berechnung des Teilverhältnisses y : x, wobei gilt:

(2/3 h_a)² = 4/9⸱3/4 a² = 1/3 a²
I  x² + 1/3 a² = y²
   a² = (x + y)² + 1/3 a²; 
II   2/3 a² = (x + y)²
2⸱I – II  2x² = 2y² – (x + y)²
             2(y²– x²) = (x + y)²
             2(y–x)(y+x) = (x+y)²
             2y – 2x = y + x
             y = 3x oder y/x = 3/1. M teilt die Strecke DN im Verhältnis 3 : 1.

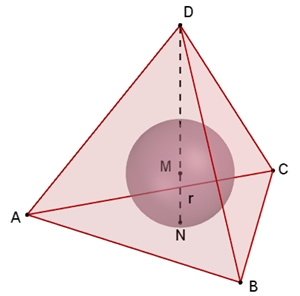
Inkugelradius r des Tetraeders:  r = 1/4 h = 1/12 √6 a ≈ 0,204 a

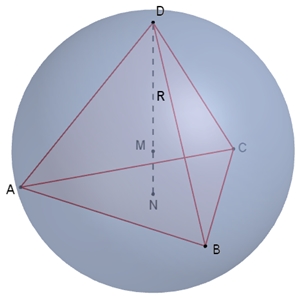
Umkugelradius R des Tetraeders:  R = 3/4 h = 1/4 √6 a ≈ 0,612 a

In- und Umkugel des Tetraeders

Oberflächen- und Volumeninhalt des Tetraeders mit der Kantelänge a:

Das Tetraeder besitzt als Oberfläche 4 gleich große gleichseitige Dreiecke.
Der Flächeninhalt A des gleichseitigen Dreiecks ist A = 1/2 a h_a = 1/4 √3 a².
Damit gilt:
Oberflächeninhalt O des Tetraeders:  O = √3 a² ≈ 1,732 a²

Der Volumeninhalt der Pyramide mit der Grundfläche A ist V = 1/3 A h.
Damit gilt:
V = 1/3 ⸱1/4 √3 a² ⸱1/3 √6 a = 1/12 √2 a³
Volumeninhalt V des Tetraeders:  V = 1/12 √2 a³ ≈ 0,118 a³

Berechnung der Winkel im Tetraeder:

Innenwinkel α des gleichseitigen Dreiecks:  α = 60° (= 180°/3).

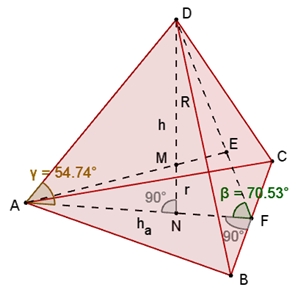
Berechnung des Winkels β zwischen benachbarten Flächen des Dodekaeders:

tan(β) = h / (1/3 h_a)
tan(β) = √6 a / (1/2 √3 a) = 2√2

Winkel β zwischen benachbarten Flächen:  β = arctan(2√2) ≈ 70,529°

Berechnung des Winkels γ zwischen Kante und Fläche eines Tetraeders:

tan(γ) = h / (2/3 h_a)
tan(γ) = √6 a / (√3 a) = √2

Winkel γ zwischen Kante und Fläche:  γ = arctan(√2) ≈ 54,735°

Zurück

Zurück zur Themenseite
Zurück zur Startseite