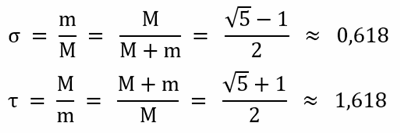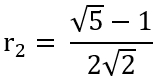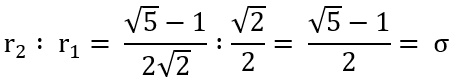|
Kreise im goldenen Schnitt
Es gelten folgende Bezeichnungen und Beziehungen:
σ
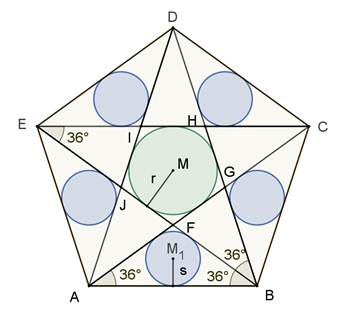
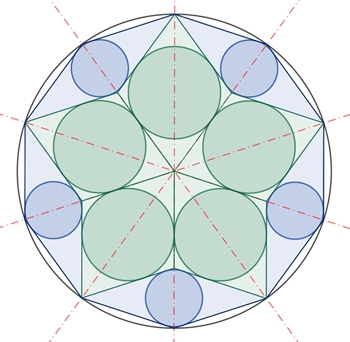
Kreise im regelmäßigen Fünfeck
Das stumpfwinklig goldene Dreieck ABF ist im
Vergleich zum stumpfwinklig goldenen Dreieck EBH um den Faktor
σ
verkleinert. da |AB| =
σ
|EB|. (siehe: Goldener
Schnitt – Konstruktionen)
Entsprechend gilt für den Radius s des blauen Kreises s =
σ
r.
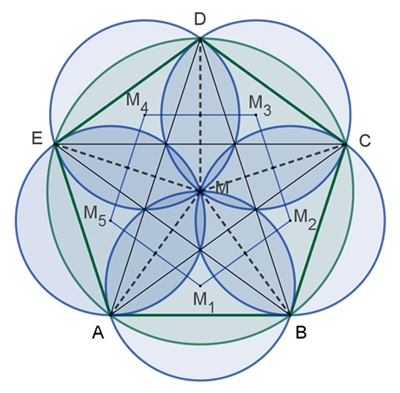
Kreise und regelmäßiges Fünfeck
Die blauen
Kreise haben alle den gleichen Radius r1
Es gilt:
r1 : r = σ
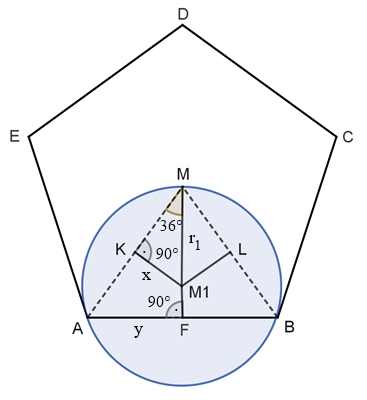
Begründungen:
K und L sind
jeweils Mittelpunkte der Strecken AM und BM.
Es sei
r = 1.
Dann gilt im
rechtwinkligen Dreieck KM1M:
cos 36° = 0,5 /
r1
⬄
r1 =
0,5 / cos 36° =
σ
Im
rechtwinkligen Dreieck KM1M gilt:
x / 0,5
= tan 36°
⬄
x = 0,5٠tan 36°
Im
rechtwinkligen Dreieck AFM gilt:
y / 1 = sin 36°
⬄
y = sin 36°
Daraus folgt:
x / y = 0,5 tan 36° / sin 36° =
0,5 / cos 36° = σ
ebenso
2x / 2y =
σ
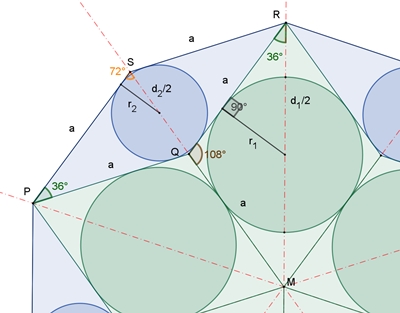
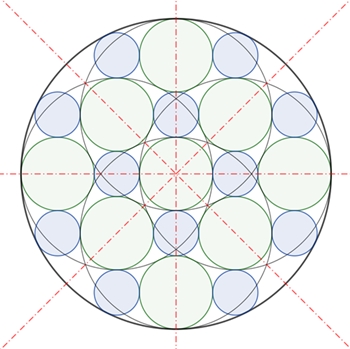
Kreise im regelmäßigen Zehneck mit der Seitenlänge a
Die blauen und die grünen Rauten haben
jeweils die Seitenlänge a.
Die Figur hat wie das reguläre Fünfeck 5
Symmetrieachsen.
Es gilt:
Die Radien bzw. Durchmesser der blauen Kreise
stehen im Vergleich zu den Radien bzw. Durchmesser der blauen Kreise im
Verhältnis des goldenen Schnitts.
Begründung:
d12 = a2 + a2 – 2a2
cos(108°) (Kosinussatz im Dreieck MRQ)
d12 = 2a2 (1 – cos(108°))
d12 = a2 (3 +
√5)/2
d1 = a
√((3 +
√5)/2)
(I)
r1 = d1/2 sin(36°)
r1 = d1/2 (√(10
- 2√5) / 4
(II)
I in II:
r1 = a √(10
+ 2√5) / 8
d22 = a2 + a2 – 2a2
cos(36°) (Kosinussatz im Dreieck PQS)
d22 = 2a2 (1 – cos(36°))
d22 = a2 (3 –
√5)/2
d2 = a
√((3 –
√5)/2)
(III)
r2 = d2/2 sin(72°)
r2 = d2/2 √(10 + 2√5)/4
(IV)
III in IV:
r2 = a
√(10
– 2√5) / 8
Damit ergibt sich für das Verhältnis
r2
r2 : r1
= (√5 – 1)/2
=
σ
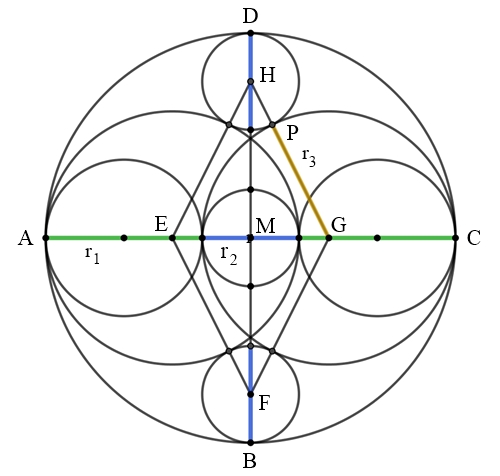
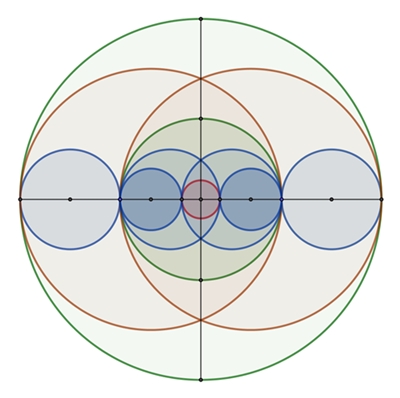
Kreise in Kreisen im goldenen Schnitt
r1 = 1,
r2 = σ,
R = 2 r1 + r2
= 2 + σ,
r3
= (2 R – 2) : 2 = 1 + σ
Kreis um H mit Radius
r2
= σ berührt den Kreis um G mit mit Radius r3 im Punkt P.
Es gilt:
R : r3
=
(2 + σ) : (1 + σ)
= (1 + τ) : τ
= 1/ τ + 1
= σ + 1
=
τ
r3
: r1
= (1
+ σ) : 1 =
τ
r1
: r2
= 1/σ = τ Die Kreisradien des jeweils größeren zum
kleineren Kreis stehen im Verhältnis der goldenen Schnittzahl
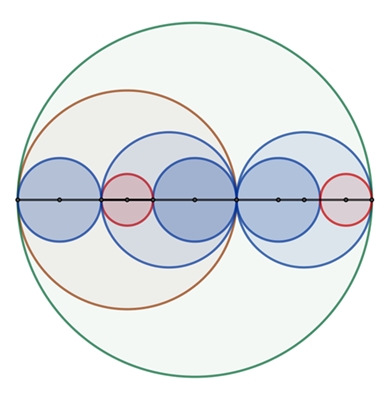
τ. Dies gilt auch für die folgenden Kreisbilder:
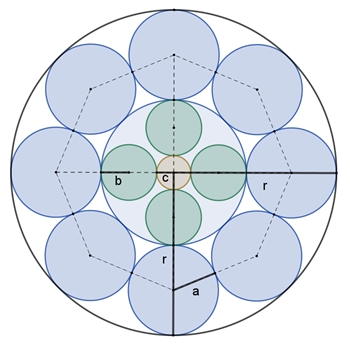
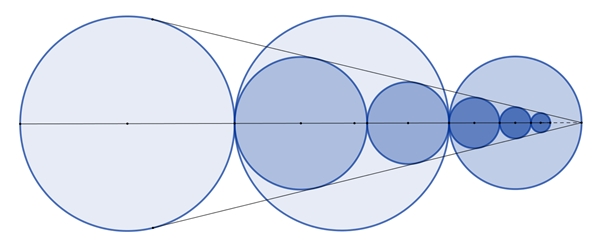
Ansatz:
r/a = 2 + τ;
a/b = τ;
b/c = τ
Begründung:
r = 2a + 2b + c; b = a/τ; c =
b/τ = a/τ²
a (2 + τ) = 2a + 2a/ τ + a/τ²
2+ τ = 2 + 2/τ + 1/τ²
τ = 2/τ + 1/τ²
τ = (2 τ + 1)/τ²
τ = τ³/ τ²
τ = τ (wahre Aussage)
Der Kreis mit Radius 2b + c
hat den τ-fachen Radius des Kreises mit Radius a.
Begründung:
(2b + c)/a = (2b + b/τ)/(b τ)
= (2 τ + 1)/τ/τ = τ³/ τ² = τ
NB : 2 τ + 1 = τ³ (s.
Goldener Schnitt –
Eigenschaften)
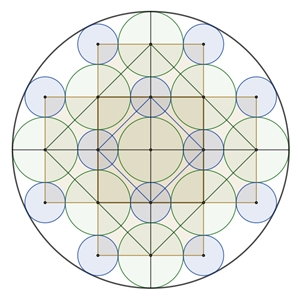
Die grünen Kreise haben den Major,
Die Figur hat 4 Symmetrieachsen wie das
Quadrat.
Deshalb sind entsprechende Mittelpunkte von
Kreisen Eckpunkte von Quadraten.
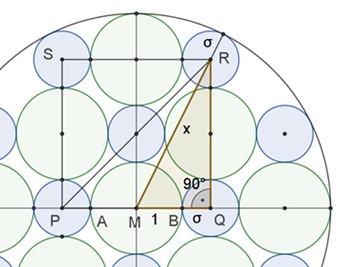
Pythagoras im △MQR: x2 = (1 + σ)2 + (2 + 2σ)2
Lässt sich vereinfachen zu: x + σ = 3 + 2σ
Dies ist der Radius des äußeren Kreises, d.h. die äußeren blauen Kreise
berühren den Umfangskreis.
Gleicharmiges Kreuz
mit Kreisen im goldenen Schnitt
Das gleicharmige Kreuz
bestehe aus 5 Quadraten (spezielles griechisches Kreuz)
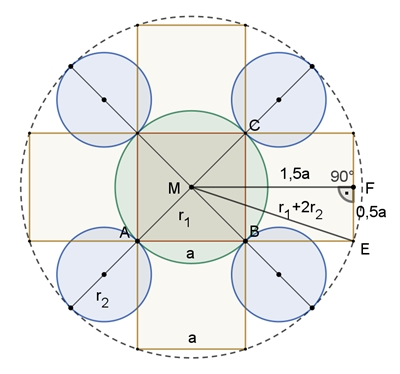
r1 = 1/2
√2 a (1) (Pythagoras im Dreieck
ABC)
(r1 + 2r2)2
= (1,5a)2 + (0,5a)2 (Pythagoras im Dreieck MEF) (r1 + 2r2)2 = 2,5 a2
2r2 =
√2,5
a – r1 (2)
(1) in (2):
2r2 =
√(5/2) a –
√2 /2 a
Die Radien stehen im Verhältnis des
goldenen Schnitts, mit dem
Major M = r1 der und dem
Minor
m = r2.
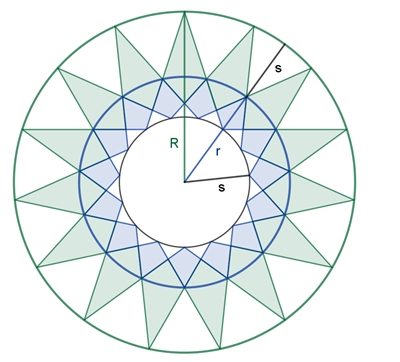
Goldener Schnitt in folgendem regelmäßigen Fünfzehneck-Stern
Es gilt: I r : R = σ
II
s : r =
σ III r + s = R
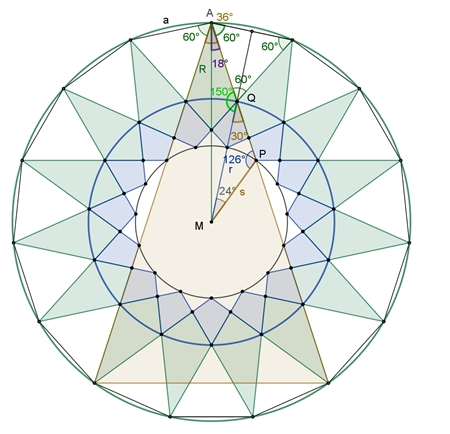
Begründung zu I:
Der Winkel an der Sternspitze ist 36°
Der Innenwinkel im regulären Fünfzehneck ist
156° = 13٠180°/15.
Damit entstehen zwischen den Spitzen
gleichseitige Dreiecke mit den Innenwinkeln 60°.
Nach dem Sinussatz gilt im Dreieck MQA:
r : R = sin(18°) : sin(150°)
Begründung zu II:
Nach dem Sinussatz gilt im Dreieck MPQ:
s : r = sin(30°) : sin(126°)
Begründung zu III:
r + s = r + r
σ = r (1 + σ) = r
τ
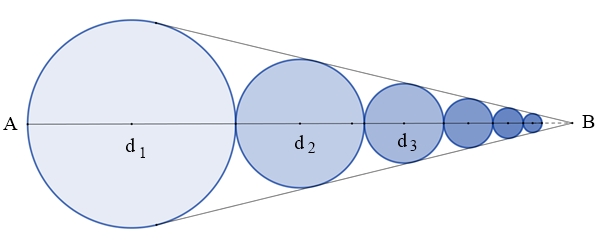
Kreiskette
d1
= 1, d2
= σ, d3
= σ٠σ = σ2,
. . . Für die geometrische Reihe mit σ < 1 gilt:
1 + σ + σ2
+ σ3
+ . . . =
1/(1- σ)
Der Flächeninhalt der Kreiskette
ist ¼ Zurück Zurück zur Startseite |