Herzkurven und Herzen

On ne voit bien qu'avec le coeur. L'essentiel est invisible pour les yeux.
Man sieht nur mit dem Herzen gut, das Wesentliche ist für die Augen unsichtbar.

Antoine de Saint-Exupery

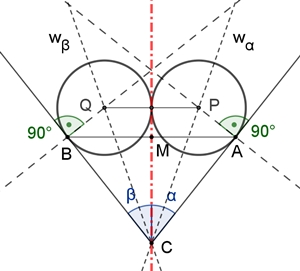
Herzkurven durch Konstruktion

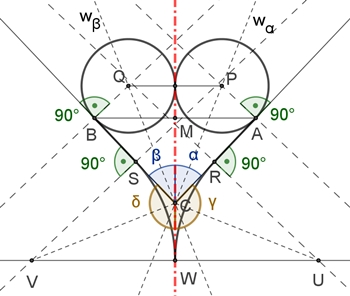
Konstruktion mit gleichschenkligem Dreieck und sich berührenden Kreisen

Gegeben ist ein gleichschenkliges Dreieck ABC.
M ist der Mittelpunkt der Strecke [AB], α = β.

w_α = Winkelhalbierende des Winkels α,
w_β = Winkelhalbierende des Winkels β.

Die beiden gleich großen Kreise mit den Mittelpunkten P und Q auf den Loten in den Punkten A und B berühren sich gegenseitig und berühren das gleichseitige Dreieck in A und B. Die Konstruktion ist symmetrisch zur Achse CM.

Mit den Randkurven entstehen Herzkurve und Herz.

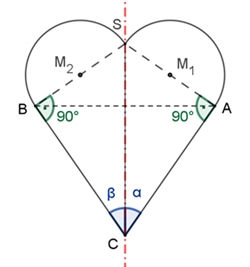
Konstruktion mit zwei gleichschenkligen Dreiecken und zwei Halbkreisen

Gegeben sind zwei gleichschenklige Dreiecke ABC und BAS (Drachenviereck CASB).
M₁ und M₂ sind der Mittelpunkte der Halbkreise über den Strecken [AS] und [BS].

AS ist senkrecht zu AC und BS ist senkrecht zu BC. CS ist Symmetrieachse der Konstruktion.

Mit den Randkurven entstehen Herzkurve und Herz. 

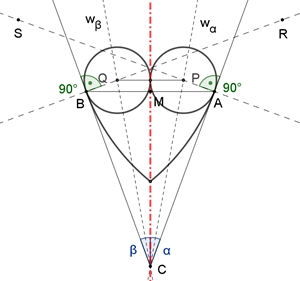
Konstruktion mit Kreisbögen und sich berührenden Kreisen

Gegeben ist ein gleichschenkliges Dreieck ABC.
M ist der Mittelpunkt der Strecke [AB], α = β.

w_α = Winkelhalbierende des Winkels α,
w_β = Winkelhalbierende des Winkels β.

Die beiden gleich großen Kreise mit Mittelpunkt P und Q berühren sich gegenseitig und berühren die Kreisbögen mit den Mittelpunkten S und R, die auf den Loten in den Punkten A und B liegen.
Die Konstruktion ist symmetrisch zur Achse CM.

Mit den Randkurven entstehen Herzkurve und Herz.

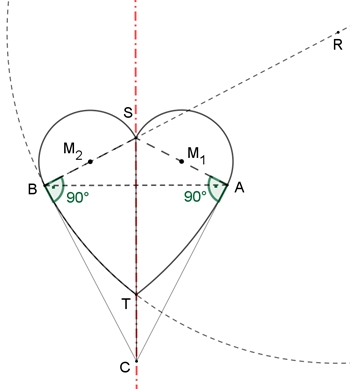
Konstruktion mit Kreisbögen und Halbkreisen

Gegeben ist das Drachenviereck CASB.
M₁ und M₂ sind der Mittelpunkte der Halbkreise über den Strecken [AS] und [BS].

AS ist senkrecht zu AC und BS ist senkrecht zu BC

R liegt auf der Halbgeraden [BS. Der Kreis um R mit Radius |BR| liefert mit der Geraden CS den Schnittpunkt T und den Kreisbogen BT.

CS ist Symmetrieachse der Konstruktion.

Mit den Randkurven entstehen Herzkurve und Herz.  

Konstruktion mit Kreisbögen, Strecken und sich berührenden Kreisen

Gegeben ist ein gleichschenkliges Dreieck ABC.
M ist der Mittelpunkt der Strecke [AB], α = β.

w_α = Winkelhalbierende des Winkels α,
w_β = Winkelhalbierende des Winkels β.

Die beiden gleich großen Kreise mit den Mittelpunkten P und Q auf den Loten in den Punkten A und B berühren sich gegenseitig und berühren die Strecken [AR] und [BS].
U ist der Schnittpunkt des Lotes in R zu AR und der Winkelhalbierenden w_𝛾 des Winkels 𝛾.
Die Konstruktion ist symmetrisch zur Achse CM.

Mit den Randkurven entstehen Herzkurve und Herz.

Herzkurven als algebraische Kurven
 
        

 Parameterform: 

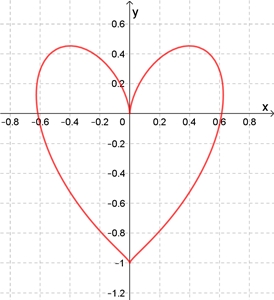
 x(t) = ± (-3t² + 2t + 1) sin(t)
 y(t) = (-3t² + 2t + 1) cos(t), 0 ≤ t ≤ 1

Flächeninhalt A der Herzkurve: A ≈ 1,133
Länge s der Herzkurve: s ≈ 4,266

Funktionen:

Flächeninhalt A der Herzkurve: A ≈ 2,356
Länge s der Herzkurve:  s ≈ 7,079

Parameterform:

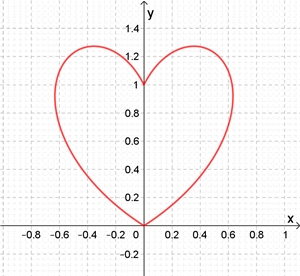
x(φ) = 5 sin³(φ) cos³(φ)
y(φ) = 5 (sin⁴(φ) – 0,2) cos²(φ), 0 ≤ φ ≤ 2π
 

Flächeninhalt A der Herzkurve: A ≈ 1,197
Länge s der Herzkurve: s ≈ 4,831

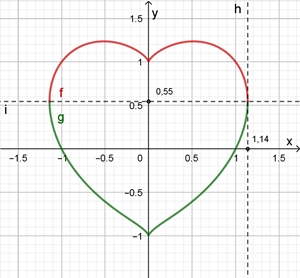
x² + (x^2/3 – y)² – 2 = 0

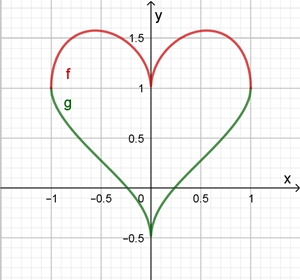
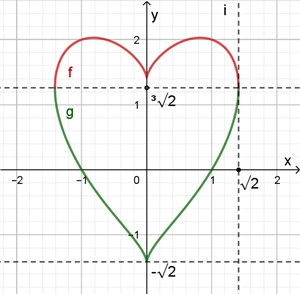
Die algebraische Kurve kann durch zwei Funktionen dargestellt werden:

Flächeninhalt A der Herzkurve: A = 2 π ≈ 6,283
Länge s der Herzkurve: s ≈ 10,501

Die algebraische Kurve kann durch zwei Funktionen dargestellt werden:

Rechter Rand: x = √2 ≈ 1,41,  y = √√2
Unterer Rand: y = –√2

Flächeninhalt A der Herzkurve: A = 2 π  ≈  6,283
Länge s der Herzkurve: s ≈ 10,705

          Herzkurve von Eugène Beutel (1909)

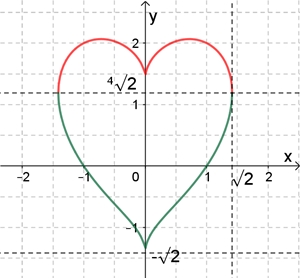
(x² + y² – 1)³ = x² y³ 
 x² + y² – 1 = x^2/3 y
 y² – x^2/3 y + x² – 1 = 0

Die algebraische Kurve lässt sich mit zwei Funktionen darstellen:

f(x) wird minimal, wenn die Wurzel gleich 0 ist, d.h. x^4/3 – 4(x² – 1) = 0.

Dies ist der Fall für x ≈ 1,1390

Flächeninhalt A der Herzkurve: A ≈ 3,662
Länge s der Herzkurve: s ≈ 7,242

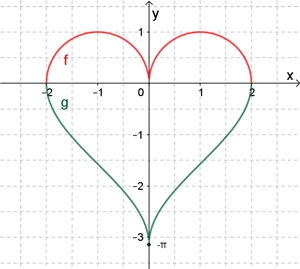
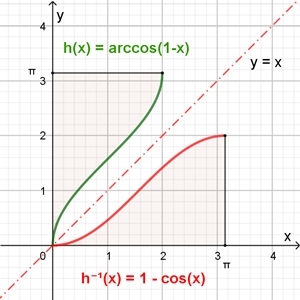
Funktionen:  

 
  g(x) = arccos(1 – |x|) – π

Flächeninhalt A der Herzkurve: A = 3π ≈ 9,4248
Länge s der Herzkurve: s ≈ 2π + 7,6404 ≈ 13,9236

Bei der Berechnung des Flächenanteils von g(x) ist es günstig das Integral der Umkehrfunktion h^-1 zur Funktion h mit der Gleichung
h(x) = g(x) + π = arccos(1 – x)  für x ≥ 0
h^-1(x) = 1 – cos(x)
zu berechnen:

Bemerkungen:

Berechnung des Flächeninhalts A einer Kurve in Parameterdarstellung mit den Grenzen a und b:

Berechnung der Länge s einer Kurve in Parameterdarstellung mit den Grenzen a und b:

Berechnung des Flächeninhalts des Funktionsgraphen einer Funktion f zwischen den Grenzen a und b und der x-Achse mit:

Berechnung der Länge s des Funktionsgraphen einer Funktion f mit den Grenzen a und b:

Zeichensatz-Herzen

In den Zeichensätzen für Programme mit Texten gibt es im Unicode Zeichensatz auch das Herz als ein Zeichen im  
Character-Code dezimal 9829 ≙ hexadezimal 2665.

Die Herzen sind in roter Farbe in Schriftgröße 72 dargestellt, daneben die Schriftart.

♥ Arial, Times New Roman,   ♥Consolas,  ♥DejaVu Sans Mono, ♥ Lucida Console,

♥ Segoe UI Semibold,   ♥ Lucida Sans Unicode,  Segoe UI Emoji

Die Kardioide

Die Kardioide ist eine spezielle Epizikloide

Parameterdarstellung der Kardioide:

x(φ) = 2a (1 – cos(φ)) cos(φ)
y(φ) = 2a (1 – cos(φ)) cos(φ)

In Polarkoordinaten gilt:

x(φ) = r(φ) cos(φ)
y(φ) = r(φ) sin(φ)

Daraus folgt die Polarkoordinatendarstellung der Kardioide: 

r(φ) = 2a (1 – cos(φ))

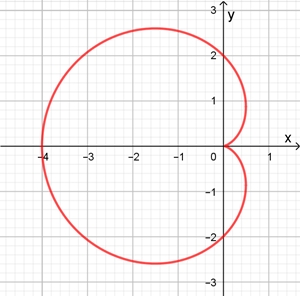
Graph der Kardioide mit a = 1

Flächeninhalt A der Kardioide: A = 6a²π

Kurvenlänge s der Kardioide: s = 16a

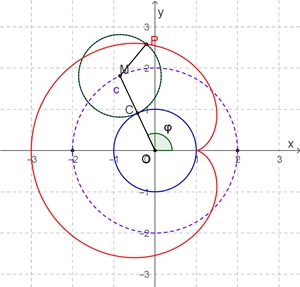
Die Kardioide entsteht durch einen abrollenden Kreis auf einem Kreis mit gleichem Radius.

Die Kardioide animiert.

Die Angaben für den Flächeninhalt A verstehen sich in LE²,
die Angaben für die Kurvenlänge in LE,
LE = Längeneinheit, z.B. 1 LE = 1 cm , 1 LE = 2 cm oder 1 LE = 1 m.

Die Berechnungen wurden mit dem CAS-Programmen wxMaxima  und Derive durchgeführt.
Bilder wurden mit Hilfe von Geogebra oder der Programmiersprache Python erstellt.

Aktuell den „Coeurs volants“ ("Flatternde Herzen", 1961) des Künstlers Marcel Duchamp (1887-1968) nachempfunden.

Vom Herzen aus Stein zum Herzen im Kaffee

Zurück
Zurück zur Startseite