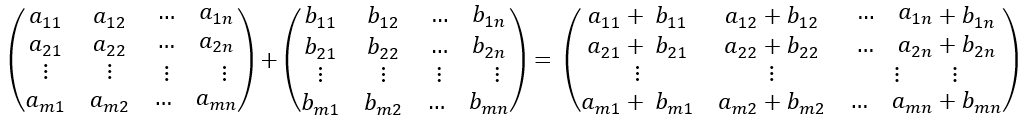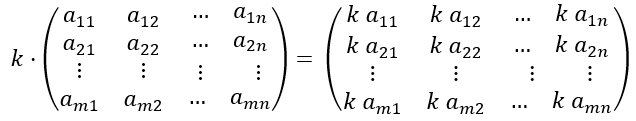Mit den Begriffen Gruppe, Halbgruppe, Ring, Körper, Vektorraum werden gemeinsame algebraische Strukturen von Mengen betrachtet, in denen die gleichen Rechenregeln gelten.

Definition von Gruppe:

Eine Gruppe (G, ⸰ )  ist eine Menge G und eine auf dieser Menge definierte Verknüpfung  „ ⸰ “,  die folgende Eigenschaften hat:

1.  (G, ⸰ ) ist abgeschlossen, d.h. für alle a, b ∊ G gilt:  a ⸰ b ist ebenfalls Element von G.

2.  (G, ⸰ ) ist assoziativ, d.h. für alle a, b, c  ∊ G gilt das Assoziativgesetz: a ⸰ (b ⸰ c) = (a ⸰ b) ⸰ c.

3.  In (G, ⸰ ) existiert ein neutrales Element e, so dass für alle a  ∊ G gilt: e ⸰ a = a ⸰ e = a.

4.  Zu jedem Element a  ∊ G existiert ein inverses Element a ^-1 ∊ G mit  a ⸰ a ^-1 = a ^-1 ⸰ a = e.

Ist die Gruppe auch kommutativ, gilt also für alle a, b ∊ G das Kommutativgesetz  a ⸰ b = b ⸰ a, so heißt die Gruppe abelsche Gruppe.

Eine nichtleere Teilmenge einer Gruppe (G, ⸰ ), die bezüglich der Verknüpfung  „ ⸰ “ selbst wieder eine Gruppe bildet, heißt Untergruppe U von G.  

Schreibweisen: "Gruppe (G, ⸰ )" oder "Gruppe G mit der Verknüpfung ⸰ ".

Beispiele für Gruppen:

Die ganzen Zahlen bilden mit der Addition als Verknüpfung die abelsche Gruppe (ℤ, + ).

Die rationalen Zahlen bilden mit der Addition als Verknüpfung die abelsche Gruppe (ℚ, + ).

Die rationalen Zahlen ohne Null bilden bezüglich der Multiplikation die abelsche Gruppe (ℚ\{0}, · ).

Die reellen Zahlen bilden bezüglich der Addition die abelsche Gruppe (ℝ, +).

Die reellen Zahlen bilden ohne Null bezüglich der Multiplikation die abelsche Gruppe (ℝ\{0}, · ).

Die Restklasse der ganzen Zahlen ℤ_n = {0, 1, 2, 3, . . ., n – 1} modulo n (ℤ_n = ℤ  mod n) ist bezüglich der Addition die
abelsche Gruppe (ℤ_n, + _{mod n}) der Ordnung n. a mod n bedeutet: Ganzzahlrest bei Division von a durch n.

Die Restklasse der ganzen Zahlen ℤ_n\{0} = {1, 2, 3, . . ., p – 1} modulo p mit Primzahl p ist bezüglich der Multiplikation die
abelsche Gruppe (ℤ_n\{0}, · _{mod p}) der Ordnung n–1.

Zyklische Gruppe, Diedergruppe, symmetrische Gruppe und Translationsgruppe.

Definition von Halbgruppe:

Eine Halbgruppe ist eine Gruppe (G, ⸰ ) , bei der das inverse und das neutrale Element fehlen. Bei einem Monoid existiert das neutrale Element.

Definition von Ring:

Ein Ring (R,+, ⸱ ) ist eine Menge R, versehen mit den zweistelligen Verknüpfungen „ + " und „⸱ “ , genannt Addition und Multiplikation, für die die folgenden Bedingungen gelten:

1.    (R, + ) ist eine abelsche Gruppe mit dem neutralen Element „0“.
     Das Negative von a wird mit –a bezeichnet, wobei gilt: a + (–a) = 0

2.    (R, · ) ist eine Halbgruppe.

3.    Es gelten die Distributivgesetze: 
     a⸱(b + c) = a⸱b + a⸱c  und  (a + b)⸱c = a⸱c + b⸱c  für alle a, b, c ∊ R

Der Ring heißt kommutativ, wenn er bezüglich der Multiplikation kommutativ ist.

Beispiele für Ringe:

Die Restklasse der ganzen Zahlen ℤ_n = {0, 1, 2, 3, . . ., n – 1} modulo n (ℤ_n = ℤ  mod n) ist ein Ring mit die abelsche Gruppe (ℤ_n, + _{mod n}) der Ordnung n bezüglich der Addition und der Halbgruppe (ℤ_n, · _{mod n}) bezüglich der Multiplikation.

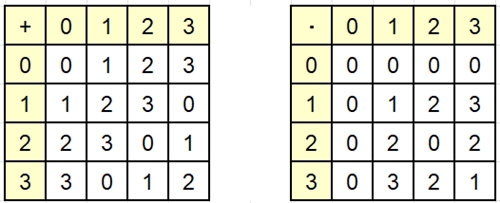
z.B. n = 4

Gruppentafel für (ℤ_n, +),      Halbgruppe (ℤ_n, · )

Bezüglich der Multiplikation gibt es zu 2 kein Inverses 2^–1 mit 2 · 2^–1 = 1 (4. Bedingung für Gruppe nicht erfüllt!)

Die Zahlen z = a + b√k mit ganzen Zahlen a, b und k bilden einen kommutativen Ring, wobei gilt:

(a₁ + b₁√k) + (a₂ + b₂√k) = ((a₁ + a₂) + (b₁ + b₂) √k

(a₁ + b₁√k) · (a₂ + b₂√k) = (a₁a₂ + b₁b₂ k) + (a₁b₂ + a₂b₁) √k

Die Menge der Polynome R[x] = a₀ + a₁x +a₂x² + … a_nxⁿ, n ∊ ℕ, a_n ∊ ℝ, bilden einen Polynomring über ℝ.

Definition von Körper:

Ein Körper (K, +, · ) ist eine Menge K, versehen mit den zweistelligen Verknüpfungen „ + “ und „⸱ “ , genannt Addition und Multiplikation, für die die folgenden Bedingungen gelten:

1.    (K, + ) ist eine abelsche Gruppe mit dem neutralen Element „0“.
     Das Negative von a wird mit –a bezeichnet, wobei gilt: a + (–a) = 0

2.    K\{0}, · ) ist eine abelsche Gruppe mit dem neutralen Element „1“.

     Das Inverse von a wird mit a^-1 = 1/a bezeichnet, wobei gilt: a⸱1/a = 1.

3.    Es gelten die Distributivgesetze: 
     a⸱(b + c) = a⸱b + a⸱c    und   (a + b)⸱c = a⸱c + b⸱c  für alle a, b, c ∊ K

Ein Körper K ist ein kommutativer Ring, bei dem  (R\{0}, · ) eine abelsche Gruppe ist.

Beispiele für Körper:

(ℚ, +, · ),  ℚ = Menge der rationalen Zahlen = Menge aller Brüche von ganzen Zahlen

(ℝ, +, · ),  ℝ = Menge der reellen Zahlen = Menge aller Brüche und Wurzeln

(ℂ, +, · ),  ℂ = Menge der komplexen Zahlen

Die Zahlen z = a + b√k mit rationalen Zahlen a, b und k bilden einen Körper, wobei gilt:

(a₁ + b₁√k) + (a₂ + b₂√k) = ((a₁ + a₂) + (b₁ + b₂) √k

Inverse Zahl der Addition zu z = a + b√k ist –z =– (a + b√k) mit z + (–z) = 0.

(a₁ + b₁√k) · (a₂ + b₂√k) = (a₁a₂ + b₁b₂ k) + (a₁b₂ + a₂b₁) √k

Inverse Zahl der Multiplikation zu z = a + b√k ist z^–1 = 1/( a + b√k) = (a – b√k)/(a² – b²k) mit z· z^–1 = 1.

Die Zahlen z = a + b√k mit reellen Zahlen a, b und k bilden ebenfalls einen Körper.

Spezialfall: k = –1, i = √–1, Menge ℂ der komplexe Zahlen z = a + b i.

Der Restklassenkörper 𝔽_p mod p, p Primzahl

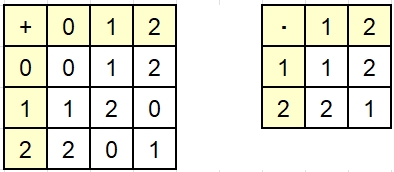
z.B. p = 3

Gruppentafeln für (𝔽_p, + ) und (𝔽_p\{0}, · )

Das Inverse bezüglich der Addition zu 1 ist 2 und zu 2 ist 1, da 1 + 2 = 0 und 2 + 1 = 0.
Das Inverse bezüglich der Multiplikation zu 1 ist 1 und zu 2 ist 2, da 2·2 mod 3 = 1.

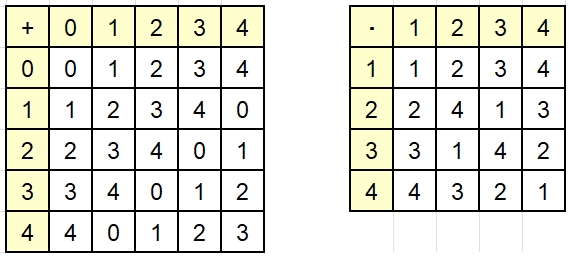
z.B. p = 5

Gruppentafel für (𝔽_p, + )                Gruppentafel für (𝔽_p\{0}, · )

Das Inverse bezüglich der Addition zu 1 ist 4, zu 2 ist 3, zu 3 ist 2 und zu 4 ist 1, da deren Summen jeweils 0 ergeben.
Das Inverse bezüglich der Multiplikation zu 1 ist 1, zu 2 ist 3, da 2·3 mod 5 = 1, zu 4 ist 4, da 4·4 mod 5 = 1.

Bemerkung: p ist eine Primzahl. Deshalb ist es nicht möglich, dass ein Produkt aus der Menge 𝔽_p\{0} die Zahl 0 ergibt.

                    a mod p bedeutet: Ganzzahlrest bei Division von a durch p.

Definition von Vektorraum

Es seien V eine Menge, (K, +, · ) ein Körper,  ⊕ : V x V ⟶ V eine Verknüpfung, genannt Vektoraddition, und ⊙ : K  x V ⟶ V eine Verknüpfung, genannt Skalarmultiplikation. Man nennt dann (V, ⊕, ⊙) einen Vektorraum über dem Körper K oder kurz K-Vektorraum, wenn für alle u, v, w ∊ V und λ, μ ∊ K die folgenden Eigenschaften gelten:

Vektoraddition:

(V, ⊕) ist eine kommutative Gruppe, d.h. es gilt:

V1  Es gilt das Assoziativgesetz: u ⊕ (v ⊕ w) = (u ⊕ v) ⊕ w.

V2  Es gilt das Kommutativgesetz: v ⊕ u = u ⊕ v.

V3  Existenz eines neutralen Elements (Nullvektror 0 ∊ V) mit v ⊕ 0 = v.

V4  Existenz eines zu v ∊ V inversen Elements –v ∊ V mit v ⊕ (– v) =  0.

Skalarmultiplikation:

S1  Es gilt das Assoziativgesetz:  (λ · μ) ⊙ v = λ ⊙ (μ ⊙ v).

S2  Es gelten die Distributivgesetze:
       (λ + μ) ⊙ v = (λ ⊙ v) ⊕ (μ ⊙ v)  und  λ ⊙ (u ⊕ v) = (λ ⊙ u) ⊕ (λ ⊙ v).

S3  Für das Einselement 1 ∊ K gilt: 1 ⊙ v = v.

Für die Vektoraddition wird zur Vereinfachung das Zeichen „+“, für die Skalarmultiplikation das Zeichen „·“ verwendet. Die Elemente des Vektorraums heißen Vektoren, die Elemente des (Skalar-)Körpers Skalare.
Ist K = ℝ, so spricht man von einem reellen Vektorraum.

Die Vektoren kann man in Kⁿ in Zeilenschreibeweise (a₁, a₂, …,  a_n) oder in Spaltenschreibweise darstellen.

Beispiele für Vektorräume

K sei ein Körper.  Dann ist Kⁿ = {(x₁, x₂, x₃, …,  x_n) mit x_i ∊ K} ein Vektorraum mittels der Vektoraddition

 (x₁,  x₂, … ,  x_n) + (y₁,  y₂, … ,  y_n) = (x₁ + y₁, x₂ + y₂, …,  x_n + y_n) und der Skalarmultiplikation λ·( x₁,  x₂, … ,  x_n) = (λ·x₁, λ·x₂, … ,  λ·x_n)

Der Nullvektor ist gleich (0, 0, … , 0) und der inverse Vektor zu

( x₁,  x₂, … ,  x_n) ist ( – x₁, – x₂, … , – x_n).

Beispiel für Vektorraum ℝ²:

a₁ = (1, 0), a₂ = (0, 1);  b₁ = (2, 1), b₂ = (–1, 1)

z = 3·(1, 0) + 4·(0, 1) = (3, 4)                                    a₁, a₂, b₁, b₂, z ∊ ℝ²

a₁ und a₂ bilden eine sog. Basis des Vektorraums, da sich als Linearkombination
von a₁ und a₂ mit  p·(1, 0) + q·(0, 1) = (p, q), p, q ∊ ℝ, jeder beliebige Vektor des Vektorraums darstellen lässt.

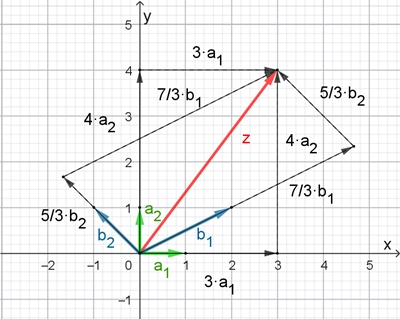
z lässt sich auch als Linearkombination von b₁ und b₂ darstellen:

x·(2, 1) + y·(–1, 1) = (3, 4).

(2x – 1, x + y) = (3, 4). Daraus folgt:

I   2x – y = 3
II  x + y = 4

I + II   3x = 7, x = 7/3
            y = 4 – 7/3, y = 5/3

z = 7/3·(2, 1) + 5/3·(–1, 1) = (3, 4).

b₁ und b₂ sind auch eine Basis des Vektorraums.

Es lässt sich jeder beliebige Vektor (p, q) des Vektorraums darstellen:

I   2x – y = p
II  x + y = q

I + II   3x = p + q,  x = (p + q)/3

            y = q – (p + q)/3,  y = (2q – p)/3

z = (p + q)/3 · (2, 1) + (2q – p)/3 · (–1, 1) = (p, q)

Veranschaulichung in der Euklidischen Ebene

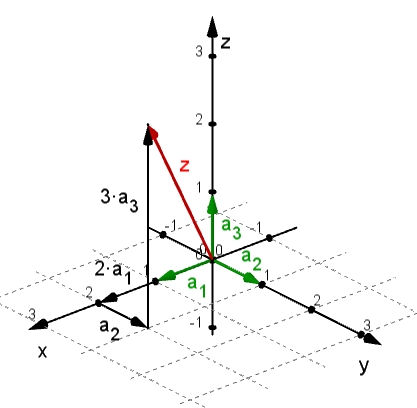
Beispiel für Vektorraum ℝ³:

a₁ = (1, 0, 0), a₂ = (0, 1, 0), a₃ = (0, 0, 1)

z = 2· a₁ + 1· a₂ + 3· a₃ = (2, 1, 3)

a₁, a₂, a₃ sind eine Basis des ℝ³.

Veranschaulichung im ℝ³

Beispiel, komplexe Zahlen:

Die komplexen Zahlen z ∊ ℂ bilden einen Vektorraum ℝ² über ℝ mit der Basis (1, 0) und (0, i):

z = a·(1, 0) + b·(0, i) = (a, bi)  ≙  a + b i

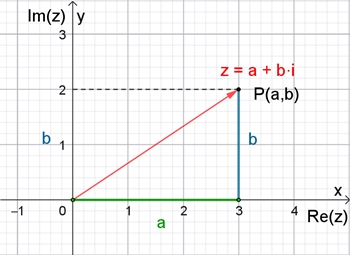
Bei der Darstellung der komplexen Zahlen in der Euklidischen Ebene wird die x-Achse zur Realteilachse (Re) von z, die y-Achse zur Imaginärteilachse (Im) von z.

Veranschaulichung in der Euklidischen Ebene

Die komplexe Zahl a + b i kann als Vektor betrachtet werden, aber auch dem Punkt P(a, b) in der Euklidischen Ebene eindeutig zugeordnet werden.

Beispiel Vektorraum der m x n - Matrizen ℝ^mxn

Vektoraddition (Matrizenaddition):

Skalarmultiplikation mit k:

a_ij mit 1≤ i ≤ m, 1≤ j ≤ m und i, j ∊ ℕ, a_ij, k ∊ ℝ

Nullvektor (Nullmatrix):