Die Kreiszahl π

   d= 2٠r  

Abrollender Kreis dynamisch

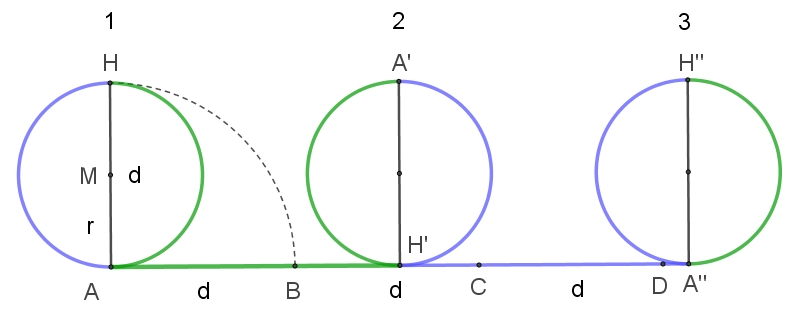
Wenn ein Kreis einmal abrollt, hat er eine Wegstrecke  zurückgelegt, die seinem Umfang entspricht und etwas länger als das Dreifache seines Durchmessers ist.

Der Faktor mit dem die Länge d des Durchmessers multipliziert wird, um die Länge U des Kreisumfangs zu erhalten, wird als Kreiszahl π (pi) bezeichnet. 

U  = d٠π  = 2r٠π,   π  ≈  3,1415926536 (auf 10 Nachkommastellen)

Näherungen im Laufe der Geschichte

Babylonier (ca. 1700 v. Chr.):               π ≈  25/8  = 3,125

Ägypter (ca. 1600 v. Chr.):                    π ≈ 256/81 ≈ 3,16

Archimedes (Grieche, ca. 250 v. Chr.):  π ≈ 22/7 ≈ 3,143

Liu Hui (Chinese, 263):                         π ≈  355/113 ≈ 3,141593

Al-Khashi (Persien, 1430):                    π ≈ 3,1415926535897932 (16 Nachkommastellen)

Ludolph van Ceulen (Köln, erst nach seinem Tod 1610 veröffentlicht):

π ≈ 3,14159265358979323846264338327950288 (35 Nachkommastellen)
Ludolph zu Ehren wurde die Kreiszahl  π lange Zeit Ludolphsche Zahl genannt.

Leonhard Euler (1748):  π auf 148 Stellen genau 

Im Jahr 2020 ist π mit Hilfe eines Computers auf 50 Billionen Nachkommastellen berechnet worden.

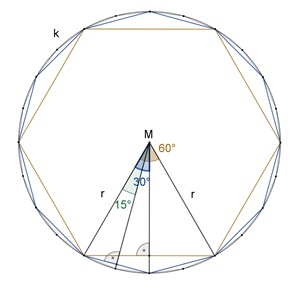
Abschätzung der Kreiszahl π durch Archimedes

A) Dem Kreis werden reguläre Vielecke einbeschrieben

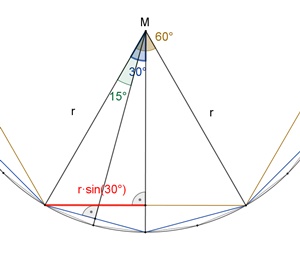
Näherung des Kreisumfangs durch den Umfang u_n regulärer einbeschriebener Vielecke für n = 6, 12, 24, 48, 96, Berechnung mit Hilfe des Sinus:

u₆  =   6٠2٠r٠sin(30°) = 2r٠3

u₁₂ = 12٠2٠r٠sin(15°) ≈ 2r٠3,1058

u₂₄ = 24٠2٠r٠sin(7,5°) ≈ 2r٠3,1326

u₄₈ = 24٠2٠r٠sin(7,5°) ≈ 2r٠3,1394

u₉₆ = 96٠2٠r٠sin(1,875°) ≈ 2r٠3,1410

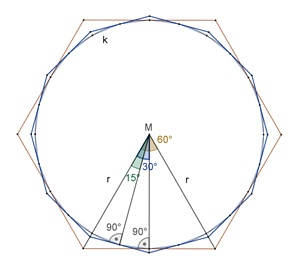
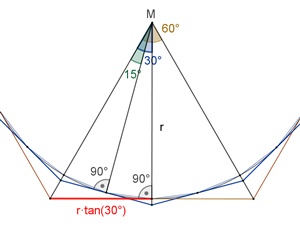
Untergrenze von π:  3,1410, Näherung durch Bruch: 3 10/71 ≈ 3,1408

B) Dem Kreis werden reguläre Vielecke umbeschrieben

Näherung des Kreisumfangs durch den Umfang u_n regulärer ubeschriebener Vielecke für n = 6, 12, 24, 48, 96, Berechnung mit Hilfe des Tangens:

u₆   =  6٠2٠r٠tan(30°) = 2r٠3,4641

u₁₂ = 12٠2٠r٠tan(15°) ≈ 2r٠3,2154

u₂₄ = 24٠2٠r٠tan(7,5°) ≈ 2r٠3,1597

u₄₈ = 48٠2٠r٠tan(3,75°) ≈ 2r٠3,1461

u₉₆ = 96٠2٠r٠tan(1,875°) ≈ 2r٠3,1427

Obergrenze von π:  3,1427, Näherung durch Bruch: 3 1/7 ≈ 3,1429

Ergebnis:

                    3,1410 < π < 3,1427  oder 

Archimedes (287-212 v. Chr) hat die Berechnungen mit Hilfe des Satzes von Pythagoras durchgeführt.
Berechnung siehe 5.Beispiel, Programmbeispiele in Python.

Formeln

Flächeninhalt A des Kreises mit Radius r:  A = r² π

Volumeninhalt V einer Kugel mit dem Radius r:  V =  r³ π

Berechnung von π als Grenzwert

Gottfried Wilhelm Leibniz (1682):

Leonhard Euler (1735):

π auf 500 Nachkommastellen (Dezimalen)

3,1415926535897932384626433832795028841971693993751058209

74944592307816406286208998628034825342117067982148086513

28230664709384460955058223172535940812848111745028410270

19385211055596446229489549303819644288109756659334461284

75648233786783165271201909145648566923460348610454326648

21339360726024914127372458700660631558817488152092096282

92540917153643678925903600113305305488204665213841469519

41511609433057270365759591953092186117381932611793105118

54807446237996274956735188575272489122793818301194912

Kein Muster in der Zahlenreihe erkennbar!

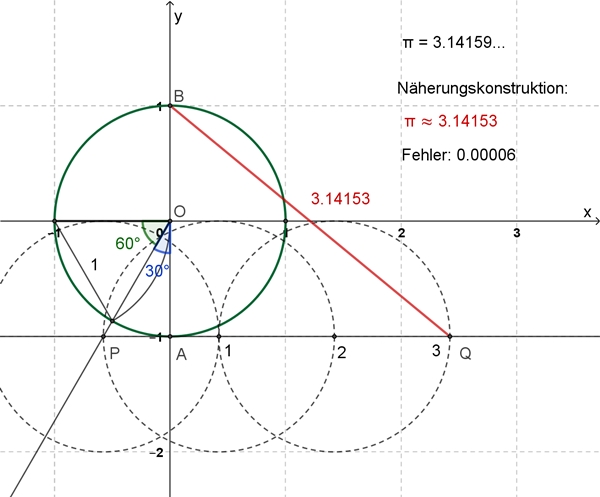
Näherungskonstruktion der Kreiszahl π durch den polnischen Mathematiker Adam Adamandy Kochański 1685

Eine bereits erstaunliche Genauigkeit. Der Fehler ist kleiner als 0,002%.

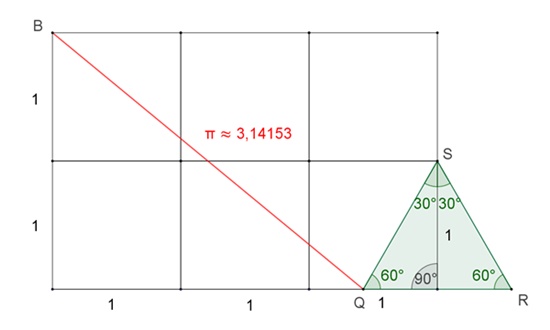
Berechnung der Streckenlänge |BQ|:

|AP| = tan 30° =

|BQ|²  =  2²  +  (3 – ( ))²  (Pythagoras im ΔAQB)

|BQ|  ≈  3,141533 

Entsprechende Konstruktion, beginnend mit dem gleichseitigen Dreieck QRS mit der Höhe h = 1 und 6 angrenzenden Quadraten der Seitenlänge 1.

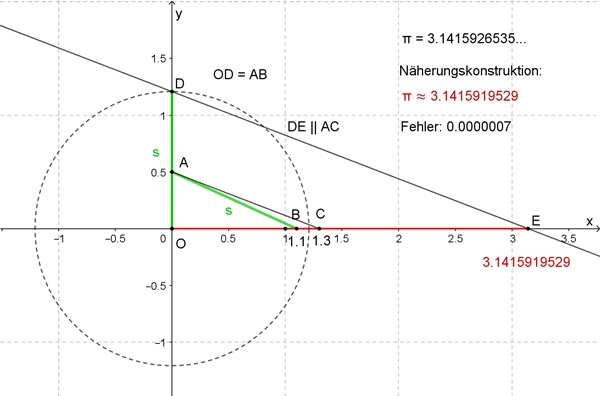
Näherungskonstruktion der Kreiszahl π durch C. G. Specht 1828

Der Fehler beträgt 0,000022%

Berechnung der Streckenlänge |OE|:

|OE| : |OD|  =  |OC| : |OA|

|OE|  =  |OC| : |OA|٠|OD|

|OE|  =  1,3 : 0,5٠  

|OE|  ≈  1,1415919529

Die Eulersche Zahl e

Die Eulersche Zahl e ist eine Konstante, die in der Analysis eine große Rolle spielt. Sie geht auf Leonhard Euler (1707 – 1783) zurück und wurde von ihm seit ca. 1727 verwendet.

Grenzwertdarstellungen von e:

n! = 1٠2٠3٠…٠ n  (n! = n Fakultät),  z.B.  4! = 1٠2٠3٠4

Eulersche Identität:
Zusammenhang mit Kreiszahl π und imaginärer Einheit i mit i² = -1:

Die Eulersche Zahl e auf 500 Nachkommastellen:

2,7182818284590452353602874713526624977572470936999595749

66967627724076630353547594571382178525166427427466391932

00305992181741359662904357290033429526059563073813232862

79434907632338298807531952510190115738341879307021540891

49934884167509244761460668082264800168477411853742345442

43710753907774499206955170276183860626133138458300075204

49338265602976067371132007093287091274437470472306969772

09310141692836819025515108657463772111252389784425056953

69677078544996996794686445490598793163688923009879312

Kein Muster in der Zahlenreihe erkennbar!

Anschauliche Bedeutung von e

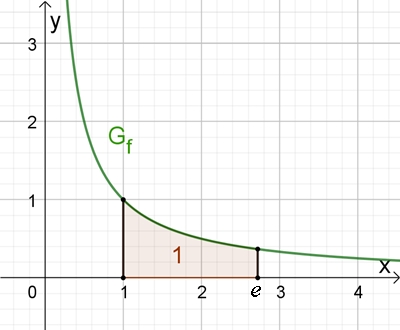
Gegeben:  f(x) = 1/x, x ϵ ℝ

Dann gilt: 

Die Fläche unter dem Graphen von f  von x = 1 bis x = e  beträgt  1 F.E.

Sowohl π als auch e sind transzendente Zahlen, da sie nicht Lösung eines Polynoms P(x) = a₀ + a₁x + a₂x² + a₃x³ + …  sind.

Außerdem sind sie irrationale Zahlen, da sie nicht als Quotient zweier ganzer Zahlen darstellbar sind.