|
Kreisringe in regelmäßigen
Vielecken
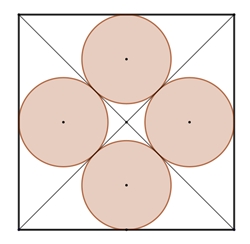
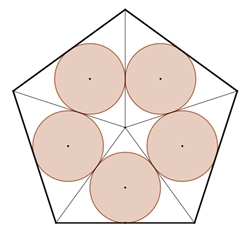
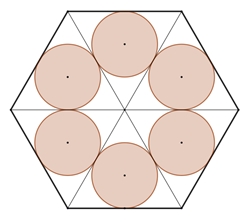
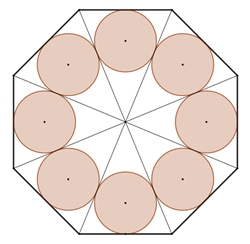
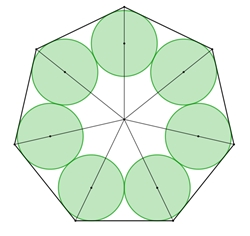
Kreisringe berühren ein reguläres n-Eck von
innen.
Anteil der Kreisflächeninhalte
zu den Flächeninhalten der n-Ecke in Abhängigkeit von n. 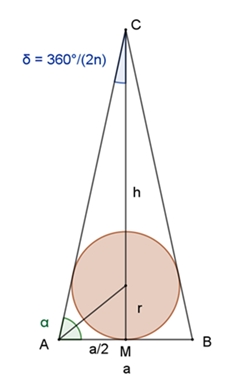
α = 90° –
360°/(2n) mit 180° =
π:
α =
π/2 –
π/n
α/2 =
π/4
–
π
/ (2n)
r /(a/2) = tan(π/4
–
π /(2n))
r = a/2٠tan(π/4
–
π /(2n))
h/(a/2) = tan(π/4
–
π /(2n))
h =
a/2٠tan(π/4
–
π /(2n))
Kreisflächeninhalt K = r2
π: K = (a/2٠tan(π/4
–
π /(2n)))2
π
Inhalt der Dreiecksfläche D =
a h/2 = a2/
(4 tan(π/n))
Flächenverhältnis n K/(n D) = K/D
K/D =
(a/2٠tan(π/4
–
π /(2n)))2
π / (a2/(4
tan(π/n)))
K/D = (tan(π/4
–
π/(2n)))2
tan(π/n)
π
Tabelle
Graphische Darstellung 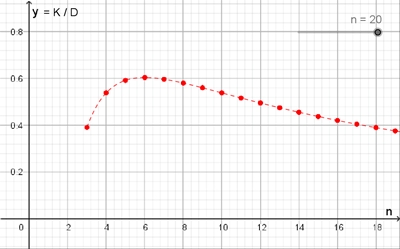
Das Maximum des Flächenverhältnisses K/D
wird für n = 6, d.h. für den Kreisring im regulären Sechseck erreicht. Das
Flächenverhältnis ist von der Seitenlänge a des regelmäßigen Vielecks
unabhängig.
Für n gegen ∞
geht K/D gegen 0.
2. Fall 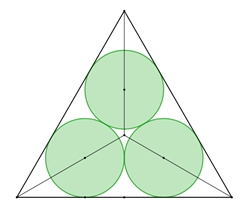 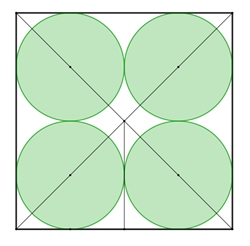
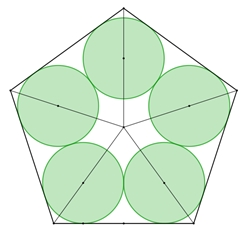 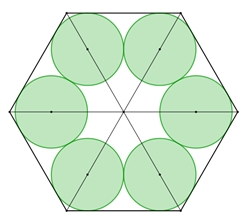
 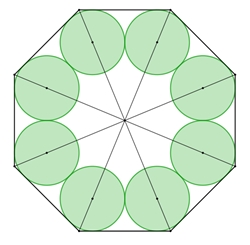 
α = 90° –
360°/(2n) und 180° =
π
α =
π/2
–
π/n
r/(1–r) = tan(π/2
–
π/n)
r = tan(π/2
–
π/n)
– r tan(π/2
–
π/n)
r (1 + tan(π/2
–
π/n))
= tan(π/2
–
π/n)
r = tan(π/2
–
π/n)
/
(1 +
tan(π/2
–
π/n))
Grüne Kreisfläche K = r2
π
Flächeninhalt Dr des Drachens ABCD = doppelter Flächeninhalt des Dreiecks
BCD
Dr = 2٠1٠h/2 = h = tan(α) = tan(π/2
–
π/n)
Flächenverhältnis n K
/
(n Dr) = K
/
Dr
K
/ Dr = (tan(π/2
–
π/n)
/
(1 +
tan(π/2
–
π/n)))2
π
/ tan(π/2
–
π/n)
Tabelle
Graphische Darstellung
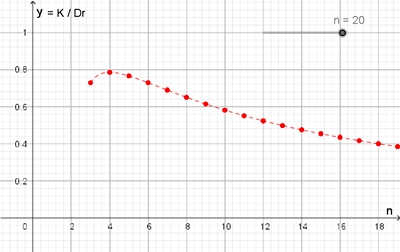
Das Maximum des Flächenverhältnisses K/Dr
wird für n = 4, d.h. für den Kreisring im Quadrat, erreicht. Das
Flächenverhältnis ist von der Seitenlänge a des regelmäßigen Vielecks
unabhängig.
Für n gegen ∞
geht K/Dr gegen 0.
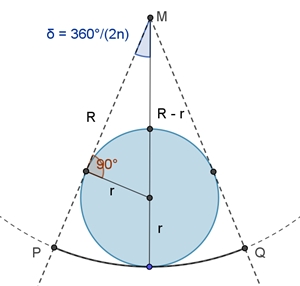
Kreisringe im Kreis
Kreisringe berühren einen Umkreis. 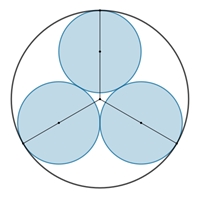 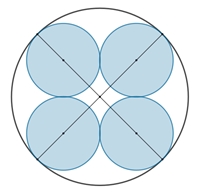 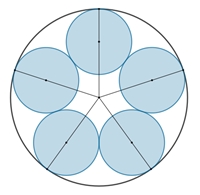 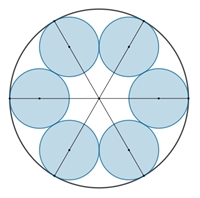 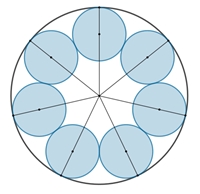 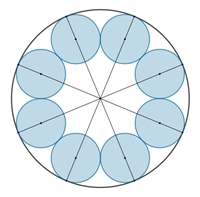
Anteil der blauen
Kreisflächeninhalte zum Flächeninhalt des Umfangskreises in Abhängigkeit von
n.
δ =
360°/ (2n)
mit 180° =
π: δ
=
π/n
r/(R
–
r) = sin(π/n)
r = R
sin(π/n)
/ (1 +
sin(π/n))
Flächeninhalt Kb der n blauen Kreise Kb = n R 2 (sin(π/n) / (1 + sin(π/n)))2 πFlächeninhalt Ku des Umfangskreises: R 2 π
Flächenverhältnis Kb/Ku: Kb/Ku = n (sin(π/n) / (1 + sin(π/n))) 2
Tabelle
Graphische Darstellung
Das Maximum des Flächenverhältnisses Kb/Ku
wird für n = 4 erreicht. Das Flächenverhältnis ist vom Radius R des
Umfangskreises unabhängig.
Für n gegen ∞
geht Kb/Ku gegen 0.
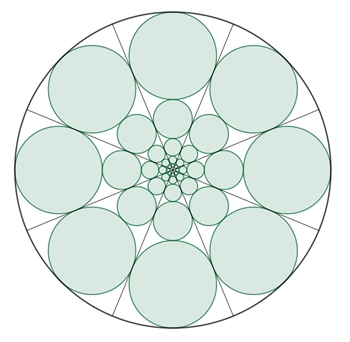
Kreisketten im regulären n-Eck
und im Kreis
(s.
Kreisketten) 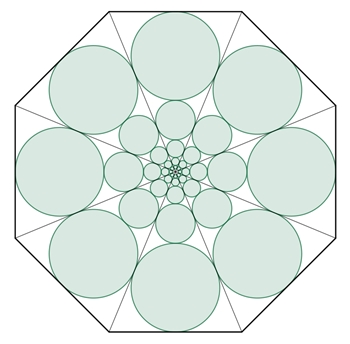
 Zurück Zurück zur Startseite |