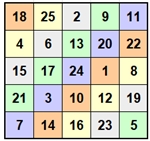
Magische Quadrate der Ordnung 5

Ein natürliches magisches Quadrat der Ordnung 5 mit den natürlichen Zahlen von 1 bis 25 besitzt 275 305 224 Grundformen (1973 von Richard Schroeppel berechnet) und 7 mal 275305224 weitere Darstellungsformen, die durch Spiegelungen und Drehungen aus den Grundformen hervorgehen. Das heißt, es gibt insgesamt 2 202 441 792 verschiedene Darstellungsformen. Auf jede der 275 305 224 Grundformen können die Abbildungen der Diedergruppe D4 angewandt werden.
Die Zeilen-, Spalten- bzw. Diagonal-Summen des magischen 5x5-Quadrats ergeben jeweils 65.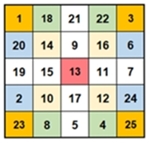
Mag_Quadrat_spez 

 

In diesem speziellen magischen 5x5-Quadrat liefern die Zahlen in den gleichfarbigen, symmetrisch liegenden Zellen zusammen mit der Zahl in der roten Zelle in der Mitte ebenfalls die Summe 65. Diese Eigenschaft bleibt bei der Anwendung der Diedergruppe D4 oder bei den Abbildungen in der Menge A erhalten.


 

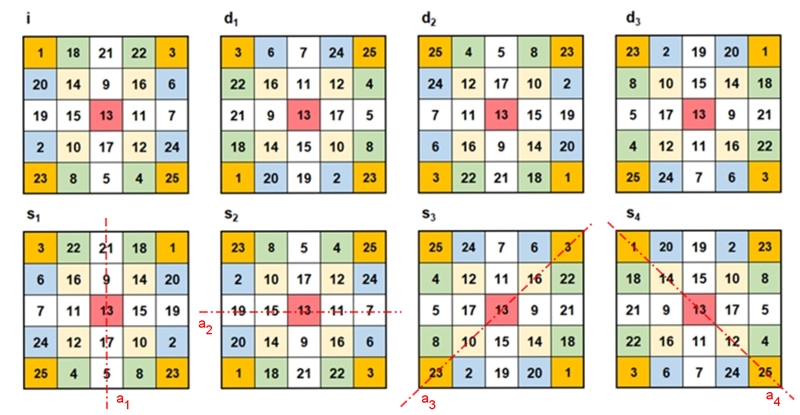
1) Die Diedergruppe D4 und das magische 5x5-Quadrat

Das vorgegebene magische Quadrat der Ordnung 5 wird als Grundform gewählt und 7 weitere Darstellungsformen entstehen durch Drehungen und Spiegelungen aus der Grundform.

Bezeichnungen:

d1,2,3   :    Drehung um 90°, 180°, 270° gegen den Uhrzeigersinn mit Drehzentrum M (Quadratmitte)

i = d4 :  identische Abbildung = Drehung um 360° gegen den Uhrzeigersinn mit Drehzentrum M.

s1,2,3,4    :   Spiegelung an der Achse a1, a2, a3, a4.

MQ5-D4

D4 = { i, d1, d2, d3, s1, s2, s3, s4 } bildet die  Diedergruppe D4 der Ordnung 8 mit der Verknüpfungstafel (Gruppentafel) siehe: Magisches 3x3-Quadrat. Die Diedergruppe D4 bildet jedes magische 5x5-Quadrat wieder auf ein magisches 5x5-Quadrat ab.

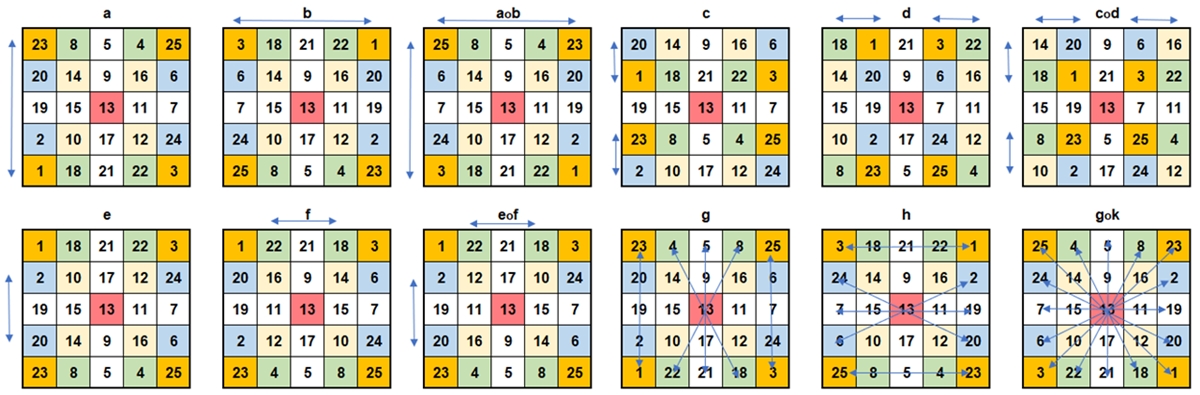
2) Weitere Abbildungen A für das spezielle magische 5x5-Quadrat

Bezeichnungen:

a :  Vertauschen der 1. und 5. Zeile.
b :  Vertauschen der 1. und 5. Spalte.
c :  Vertauschen der 1. und 2 und der 4. und 5. Zeile.
d :  Vertauschen der 1. und 2 und der 4. und 5. Spalte.
e :  Vertauschen der 2. und 4. Zeile.
f :  Vertauschen der 2. und 4. Spalte.
g, h, goh :  Vertauschen wie in den magischen Quadraten angezeigt
 o :  Verknüpfung zweier Abbildungen

Die Menge der Abbildungen A = {a, b, aob, c, d, cod, e, f, eof, g, h, goh} bildet das spezielle magische 5x5-Quadrat wieder auf ein spezielles magisches 5x5-Quadrat ab.

Abbildungen a-h                                           

Bei diesen speziellen magischen Quadraten kann man sich auf Grund der Abbildungen A mit einer geringeren Zahl (1/12) an Grundformen begnügen.

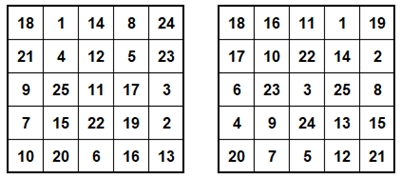
Weitere Beispiele für zufällig ausgewählte magische Quadrate der Ordnung 5.

a) Magische 5x5-Quadrate mit den gleichen speziellen Eigenschaften

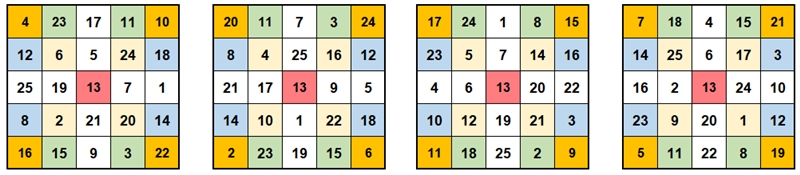
MG5-4spez

b) Pandiagonale magische 5x5-Quadrate

MQ5-4pan

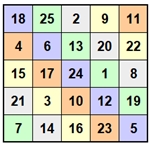
c) Magische 5x5-Quadrate ohne weitere Eigenschaften

MQ5-2allg 

 

Hier liefert die Menge der Abbildungen A keine magischen Quadrate.

 

 

Bemerkung:

Die große Anzahl von magischen Quadraten der Ordnung 5 überrascht zunächst.

Begründet ist dies durch die große Anzahl der möglichen Anordnungen von 25 verschiedenen Zahlen.

Die natürlichen Zahlen von 1 bis 25 können auf  25! = 1٠2٠3٠... ٠25 = 15511210043330985984000000 verschiedene Anordnungen aneinandergereiht werden oder in einem 5x5-Quadrat die 5 mal 5 Zeilen ausfüllen.

Der Anteil der magischen Quadrate beträgt dabei nur
2202441792 / 15511210043330985984000000 ≈ 1,4٠10-16.


Zurück
Zurück zur Startseite