|
Klassifizierung von Parketten (Kachelungen, englisch: Tessellation) Periodische Parkettierungen
Ein Parkettstein (Kachel) ist eine Figur, die durch eine endlich lange sich
nicht schneidende Linie eingeschlossen wird. Bedecken diese Parkettsteine
eine Ebene lückenlos und ohne Überlappungen, spricht man von einer
Parkettierung (Kachelung).
Hier werden nur Parkettsteine mit geradlinigen Kanten
betrachtet und Parkettsteine durch Vielecke (Dreieck,
Viereck, Fünfeck und Sechseck) dargestellt. Bei der Klassifizierung von Parketten mit kongruenten
Parkettsteinen spielen die Eckpunkte eine entscheidende Rolle. Umläuft man einen einzelnen Parkettstein gegen den
Uhrzeigersinn und notiert für jeden Eckpunkt seinen Wert, so erhält man eine
Sequenz von natürlichen Zahlen, die bis auf zyklische Vertauschungen für
alle Parkettsteine des Parketts dieselbe ist. Man bezeichnet diese Sequenz
der Wertigkeiten der Eckpunkte auch als Knüpfmuster des
betreffenden Parketts. Dieses Knüpfmuster kennzeichnet das Parkett. Man kann sich die Struktur des Parketts auch als ein
dehnbares Netz aus Fäden und Knoten, den Eckpunkten, vorstellen. Eine
Verzerrung des Netzes ändert nichts an den Eigenschaften der Knoten des
Netzes.
Der Mineraloge und Kristallograph Fritz
Laves zeigte 1931, dass es genau 11 verschiedene Knüpfmuster für Parkette
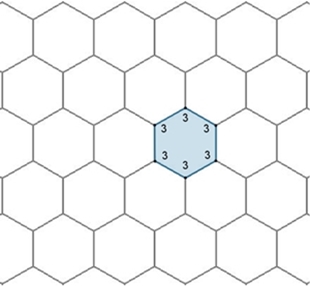
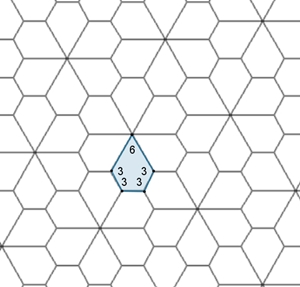
gibt. Parkett 1: (3,3,3,3,3,3) Parkett 2: (3,3,3,3,6)
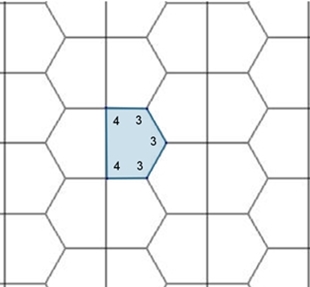
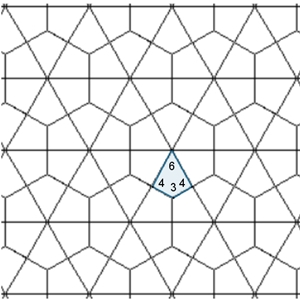
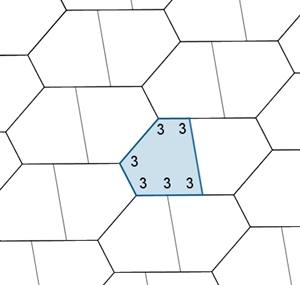
Parkett 3: (3,3,3,4,4)
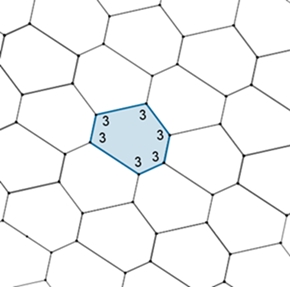
Parkett 1
kann auch mit
einem asymmetrischen Sechseck oder
einem Fünfeck als Parkettstein dargestellt werden.
Beispiel:
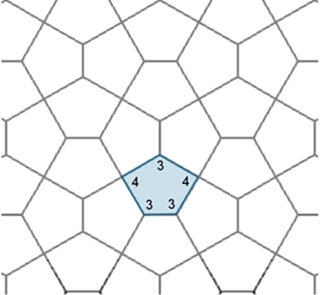
Bei der Parkettierung mit Fünfecken als
Parkettsteine wurden bisher 15 verschiedene Fünfeckformen gefunden. Sie
können verschiedenen Knüpfmustern zugeordnet werden.
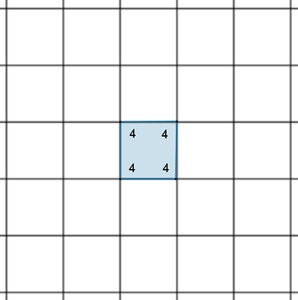
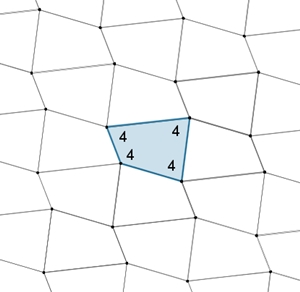
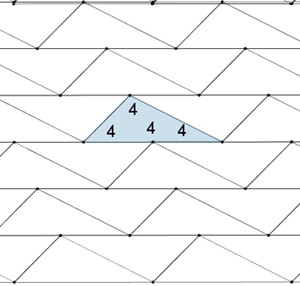
In Parkett 7 wird der
Parkettstein durch ein Quadrat dargestellt. Der Parkettstein kann aber auch
ein beliebiges konvexes Viereck oder ein
Dreieck sein.
Beispiel:
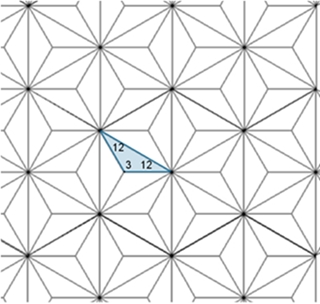
Der Parkettstein für Parkett 5
ist ein konvexer Drachen mit den Innenwinkeln 60°, 90°, 120° und 90°.
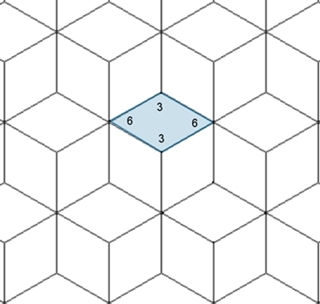
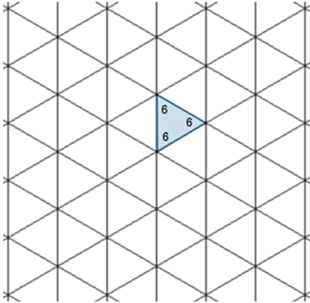
Der Parkettstein für Parkett 6
ist eine Raute mit den Innenwinkeln 60° und 120°
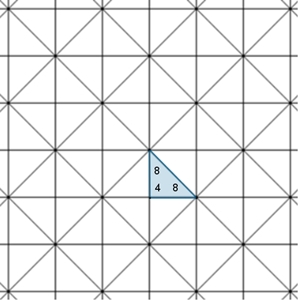
Der Parkettstein für Parkett 8
ist ein gleichschenklig rechtwinkliges Dreieck.
Der Parkettstein für Parkett 9
ist ein gleichschenkliges Dreieck mit den Basiswinkeln 30°.
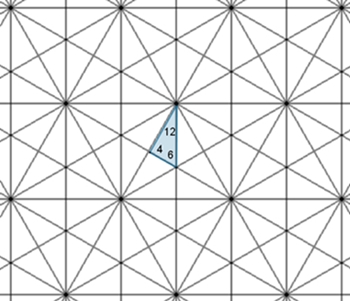
Der Parkettstein für Parkett 10
ist ein rechtwinkliges Dreieck mit den weiteren Innenwinkeln 30° und 60°.
Der Parkettstein für Parkett 11
ist ein beliebiges Dreieck Parkettierungen können aber auch an Hand von Gruppeneigenschaften klassifiziert werden. Dies führt zu den
17
Symmetriegruppen eines periodischen Musters.
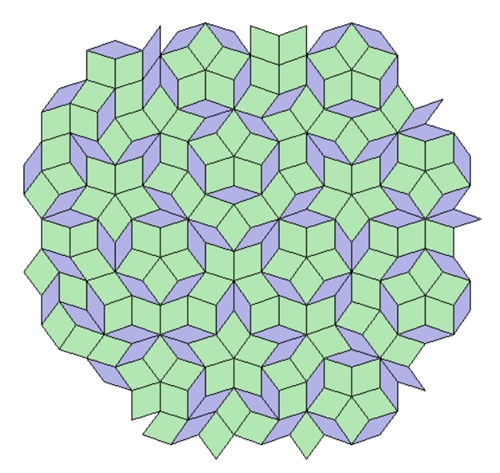
Nicht-periodische Parkettierungen Professor Sir Roger
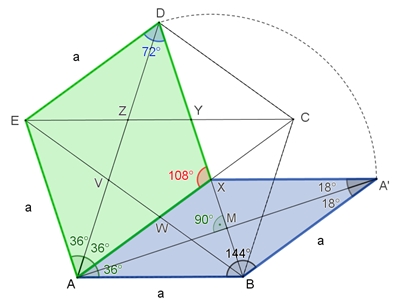
Penrose hat 1974 mit Hilfe zweier Kacheln (große und kleine Raute) eine
nicht-periodische
Parkettierung erzeugt. Eine nicht-periodische Penrose-Parkettierung
Große und kleine Raute im regulären Fünfeck
Mit einer Pfeil-Kachel kann man sowohl nicht-periodische wie periodische Parkettierungen erzeugen.
Nicht-periodische Parkettierung,
periodische Parkettierung mit der
Pfeil-Kachel
Pfeile in gleicher Richtung werden mit
gleicher Farbe gekennzeichnet.
Der pensionierte Druckanlagentechniker
David
Smith hat im November 2022 die Hut-Kachel (engl. hat-tile) entworfen, die
als einzelner Parkettstein (Einstein-Kachel) die Ebene vollständig
nicht-periodisch parkettiert und es gibt damit keine periodische
Parkettierung. Dabei müssen aber auch gespiegelte Parkettsteine zugelassen
werden.
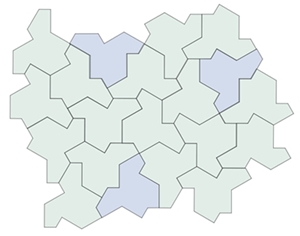
Nicht-periodische Parkettierug mit
Hut-Kacheln (gespiegelte Kacheln blau)
Eine neu entwickelte Kachel mit der
Bezeichnung Spectre soll nur eine nicht-periodische
Parkettierung mit nur einer Kachel (Einstein-Kachel) erzeugen, gefunden im Mai 2023
von David Smith, Joseph Samuel Myers, Craig S. Kaplan und Chaim
Goodman-Strauss.
Nicht-periodische Parkettierug mit
Spectre-Kacheln
Quellen:
Spektrum der Wissenschaften 10.23: Der doppelte Einstein
Vampir-Kachel löst den
«Einstein» ab - Galaxus
Animierte Parkette
Eine Parkettierung der Ebene besteht aus einer Menge
von Parkettsteinen oder Grundmustern, die die Ebene ohne Überlappungen und ohne
Lücken bedeckt.
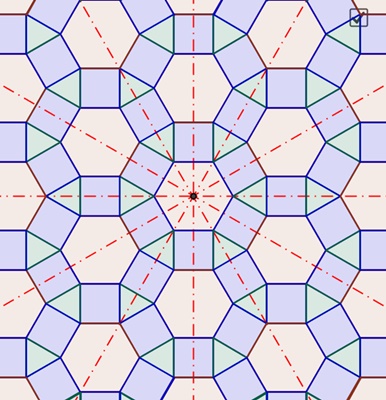
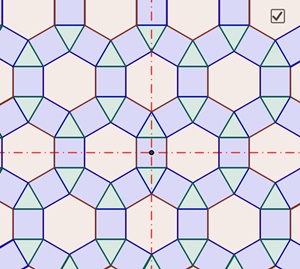
Muster der Gruppe p6m mit 6 Symmetrieachsen und sechszähliger Rotation:
Animation des
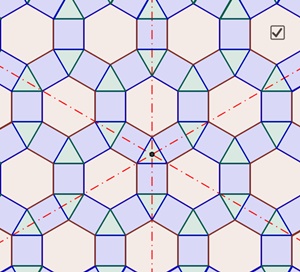
Musters der Gruppe p6m Untergruppen von p6m mit 3 Symmetrieachsen und dreizähliger Rotation und mit 2 Symmetrieachsen und zweizähliger Rotation:
Animation linkes Muster Animation rechtes Muster
Als Grundmuster werden bei den folgenden Bildern Rauten und Quadrate verwendet:
Bayerisches Rautenmuster als Vorlage für eine Parkettierung:
Bilder erstellt mit GeoGebra
Literatur- und Quellenangaben: Parkettierung
https://de.wikipedia.org/wiki/Parkettierung Parkettierungen im Matheunterricht
http://othes.univie.ac.at/36556/1/2015-01-21_0509371.pdf Frank Heinrich:
Parkettierungen I
http://www.mathematikinformation.info/pdf/MI39Heinrich.pdf Zurück Zurück zur Startseite |
