Primzahlenmuster

Es werden gleich lange Reihen von natürlichen Zahlen gebildet.
Primzahlen werden durch ●, Nichtprimzahlen durch + dargestellt.

    Zeilenbreite 30,  Zahlen von 1 bis 1200

  +●●+●+●+++●+●+++●+●+++●+++++●+

  ●+++++●+++●+●+++●+++++●+++++●+

  ●+++++●+++●+●+++++●+++●+++++●+

  ++++++●+++●+●+++●+●+++●+++++++

  ++++++●+++●+++++●+●+++++++++●+

  ●+++++●+++++●+++●+++++●+++++●+

  ●+++++++++●+●+++●+●+++++++++++

  ●+++++++++++●+++●+●+++●+++++●+

  ●+++++++++●+++++●+++++●+++++●+

  ●+++++●+++●+●+++++++++●+++++++

  ++++++●+++●+●+++●+++++++++++++

  ●+++++●+++++++++●+●+++●+++++●+

  ++++++●+++++●+++++●+++●+++++●+

  ++++++●+++●+++++++●+++++++++●+

  ●+++++++++●+●+++++●+++●+++++●+

  ++++++●+++●+●+++●+++++++++++●+

  ++++++●+++●+++++++●+++●+++++●+

  ++++++++++●+●+++++++++++++++++

  ●+++++●+++++++++●+++++●+++++●+

  ●+++++●+++++++++●+++++●+++++●+

  ●+++++●+++++●+++●+●+++++++++++

  ●+++++++++●+●+++●+++++●+++++●+

  ●+++++++++++●+++●+++++●+++++++

  ●+++++++++●+++++++●+++++++++●+

  ++++++●+++++●+++++●+++●+++++++

  ●+++++●+++●+++++++●+++●+++++++

  ++++++●+++++++++●+++++++++++●+

  ●+++++++++●+●+++●+●+++++++++●+

  ++++++++++++●+++●+●+++●+++++++

  ++++++●+++●+●+++●+++++++++++++

  ++++++●+++●+++++++●+++++++++●+

  ++++++●+++●+++++●+++++●+++++++

  ++++++●+++●+++++●+++++●+++++++

  ●+++++●+++++++++++●+++●+++++●+

  ●+++++++++●+●+++++●+++++++++●+

  ●+++++++++●+●+++++●+++++++++++

  ++++++●+++●+●+++●+++++●+++++●+

  ++++++●+++++●+++++●+++++++++++

  ++++++++++●+●+++++++++●+++++++

  ●+++++++++●+++++●+++++●+++++++

   Primzahlen insgesamt:  196

     Zeilenbreite 30,  1200 Zahlen von 99 991  bis 101 190

  ●+++++++++++●+++++++++++++++●+

  ++++++++++++++++++++++●+++++●+

  ++++++●+++++++++++●+++++++++++

  ++++++++++++++++++++++●+++++●+

  ++++++++++++++++++●+++++++++++

  ++++++++++●+●+++++++++++++++●+

  ++++++++++++●+++++●+++●+++++++

  ++++++●+++++●+++++++++++++++++

  ++++++●+++++++++++++++++++++++

  ++++++●+++●+++++++●+++++++++++

  ●+++++●+++++++++++++++●+++++++

  ++++++++++++●+++++++++●+++++++

  ++++++●+++●+●+++++++++++++++●+

  ++++++++++●+●+++++++++●+++++++

  ●+++++●+++++++++++++++++++++++

  ++++++●+++++++++++●+++++++++●+

  ++++++++++++●+++++++++●+++++++

  ●+++++++++●+++++●+●+++●+++++++

  ++++++●+++++++++●+●+++++++++●+

  ++++++++++++++++++++++++++++++

  ●+++++++++++++++++●+++●+++++++

  ●+++++++++++++++++++++++++++●+

  ++++++++++++++++++●+++●+++++++

  ++++++++++++●+++++●+++●+++++++

  ++++++++++++++++++++++●+++++++

  ●+++++●+++++++++++++++++++++●+

  ++++++++++++++++●+++++++++++●+

  ●+++++++++●+++++++++++●+++++●+

  ++++++++++++++++●+++++●+++++++

  ++++++++++++++++++++++++++++++

  ++++++++++++++++●+++++●+++++++

  ++++++●+++●+++++●+++++●+++++++

  ++++++●+++++++++++++++++++++++

  ●+++++●+++++++++++●+++++++++●+

  ++++++++++●+++++●+++++++++++++

  ++++++++++●+++++++++++●+++++++

  ++++++++++●+++++++●+++++++++++

  ++++++●+++●+●+++●+●+++++++++++

  ++++++++++●+++++++●+++++++++●+

  ●+++++++++++●+++++++++●+++++++

   Primzahlen insgesamt:  100

Bereits aus der Primzahlfunktion ergibt sich, dass die Anzahl der Primzahlen
in gleich breiten Intervallen mit zunehmender Größe abnimmt.

Bei gerader Zeilenbreite sind die Primzahlen in senkrechter Richtung angeordnet.

     Zeilenbreite 43,  Zahlen von 1 bis 1978

  +●●+●+●+++●+●+++●+●+++●+++++●+●+++++●+++●+●

  +++●+++++●+++++●+●+++++●+++●+●+++++●+++●+++

  ++●+++++++●+++●+●+++●+●+++●+++++++++++++●++

  +●+++++●+●+++++++++●+●+++++●+++++●+++●+++++

  ●+++++●+●+++++++++●+●+++●+●+++++++++++●++++

  +++++++●+++●+●+++●+++++●+●+++++++++●+++++●+

  ++++●+++++●+●+++++●+++●+●+++++++++●++++++++

  +++++●+++●+●+++●+++++++++++++●+++++●+++++++

  ++●+●+++●+++++●+++++++●+++++●+++++●+++●++++

  +●+++++++●+++●+++++++●+++++++++●+●+++++++++

  ●+●+++++●+++●+++++●+++++++●+++●+●+++●++++++

  +++++●+++++++●+++●+++++++●+++●+++++●+++++++

  ++++●+●+++++++++++++++++●+++++●+++++++++●++

  +++●+++++●+●+++++●+++++++++●+++++●+++++●+●+

  ++++●+++++●+++●+●+++++++++++●+++++++++●+●++

  +●+++++●+++++●+●+++++++++++●+++●+++++●+++++

  ++●+++++++++●+++++++●+++++++++●+++++++●++++

  +●+++++●+++●+++++++●+++++●+++●+++++++●+++●+

  ++++++++++++●+++++++++●+++++++++++●+●++++++

  +++●+●+++●+●+++++++++●+++++++++++++●+++●+●+

  ++●+++++++++++++●+++●+●+++●++++++++++++++++

  +++●+++●+++++++●+++++++++●+++++++●+++●+++++

  ●+++++●+++++++++++++●+++●+++++●+++++●++++++

  +●+++++●+++++++++++●+++●+++++●+●+++++++++●+

  ●+++++●+++++++++●+●+++++++++●+●+++++●++++++

  +++++++++++●+++●+●+++●+++++●+++++●+++++++●+

  ++++●+++++●+++++++++++++++++++++●+●++++++++

  +●+++++++●+++++++++●+++++●+++++●+++++++●+++

  ++++++++●+++●+++++●+++++●+●+++++●++++++++++

  +●+++++++++●+++++++++++++++++●+●+++●+++++●+

  ●+++++●+++●+●+++●+++++++++++●+●+++++●++++++

  +++++++++++++++++++++++++++●+++++●+++++●+++

  ++++●+++++++++++++++++●+++++++++●++++++++++

  +++●+++●+●+++●+++++●+++++++●+++●+●+++++●+++

  ++++++++●+++++++++●+●+++●+●+++●+++++●++++++

  +++++●+++++++++++●+++++++●+++++++++++●+++++

  ●+++●+++++●+++++++●+++●+++++++●+++●++++++++

  +++++●+++●+++++●+●+++●+++++●+●+++++●+++++++

  ++●+++++++++++++++++++●+++++●+++●+●++++++++

  +++++++++++++++●+++●+●+++++++++●+++++++++++

  ●+●+++++++++●+++++++●+++++●+++++●+++++●++++

  +++++++++++++●+++++●+++●+●+++++++++++●+++++

  ++++●+++++++++++●+++++++●+++++++++++++++●++

  +++++++++++●+++++●+++●+●+++●+●+++++++++●+++

  ++++++++●+++++●+++++●+++++++++++++++++●+●++

  +++++++++++++●+●+++++++++++++++++++++●+++++

Die Primzahlen sind hier vorzugsweise in diagonaler Richtung von rechts oben nach links unten angeordnet.

     Zeilenbreite 55,  Zahlen von 1 bis 2970

  +●●+●+●+++●+●+++●+●+++●+++++●+●+++++●+++●+●+++●+++++●++

  +++●+●+++++●+++●+●+++++●+++●+++++●+++++++●+++●+●+++●+●+

  ++●+++++++++++++●+++●+++++●+●+++++++++●+●+++++●+++++●++

  +●+++++●+++++●+●+++++++++●+●+++●+●+++++++++++●+++++++++

  ++●+++●+●+++●+++++●+●+++++++++●+++++●+++++●+++++●+●++++

  +●+++●+●+++++++++●+++++++++++++●+++●+●+++●+++++++++++++

  ●+++++●+++++++++●+●+++●+++++●+++++++●+++++●+++++●+++●++

  +++●+++++++●+++●+++++++●+++++++++●+●+++++++++●+●+++++●+

  ++●+++++●+++++++●+++●+●+++●+++++++++++●+++++++●+++●++++

  +++●+++●+++++●+++++++++++●+●+++++++++++++++++●+++++●+++

  ++++++●+++++●+++++●+●+++++●+++++++++●+++++●+++++●+●++++

  +●+++++●+++●+●+++++++++++●+++++++++●+●+++●+++++●+++++●+

  ●+++++++++++●+++●+++++●+++++++●+++++++++●+++++++●++++++

  +++●+++++++●+++++●+++++●+++●+++++++●+++++●+++●+++++++●+

  ++●+++++++++++++●+++++++++●+++++++++++●+●+++++++++●+●++

  +●+●+++++++++●+++++++++++++●+++●+●+++●+++++++++++++●+++

  ●+●+++●+++++++++++++++++++●+++●+++++++●+++++++++●++++++

  +●+++●+++++●+++++●+++++++++++++●+++●+++++●+++++●+++++++

  ●+++++●+++++++++++●+++●+++++●+●+++++++++●+●+++++●++++++

  +++●+●+++++++++●+●+++++●+++++++++++++++++●+++●+●+++●+++

  ++●+++++●+++++++●+++++●+++++●+++++++++++++++++++++●+●++

  +++++++●+++++++●+++++++++●+++++●+++++●+++++++●+++++++++

  ++●+++●+++++●+++++●+●+++++●+++++++++++●+++++++++●++++++

  +++++++++++●+●+++●+++++●+●+++++●+++●+●+++●+++++++++++●+

  ●+++++●+++++++++++++++++++++++++++++++++●+++++●+++++●++

  +++++●+++++++++++++++++●+++++++++●+++++++++++++●+++●+●+

  ++●+++++●+++++++●+++●+●+++++●+++++++++++●+++++++++●+●++

  +●+●+++●+++++●+++++++++++●+++++++++++●+++++++●+++++++++

  ++●+++++●+++●+++++●+++++++●+++●+++++++●+++●++++++++++++

  +●+++●+++++●+●+++●+++++●+●+++++●+++++++++●+++++++++++++

  ++++++●+++++●+++●+●+++++++++++++++++++++++●+++●+●++++++

  +++●+++++++++++●+●+++++++++●+++++++●+++++●+++++●+++++●+

  ++++++++++++++++●+++++●+++●+●+++++++++++●+++++++++●++++

  +++++++●+++++++●+++++++++++++++●+++++++++++++●+++++●+++

  ●+●+++●+●+++++++++●+++++++++++●+++++●+++++●++++++++++++

  +++++●+●+++++++++++++++●+●+++++++++++++++++++++●+++++●+

  ++++++●+++++●+++●+●+++●+++++++●+++++●+++++++++●+●++++++

  +++●+++++++++++++●+++++++++●+++++●+++++++++++●+●+++●+●+

  ++++++++●+++++++++++●+●+++++++++++++++●+●+++++●+++●+●++

  +++++++●+++++++●+++++++++++++++++●+++++++++++++++++++++

  ++●+++●+++++●+++++++●+++++++++++++++●+●+++●+++++++●++++

  +++++++++++●+●+++●+++++++●+++++●+++++●+++●+++++++++++●+

  ●+++++++++++++++++++++●+++++●+●+++++●+++●+++++●++++++++

  +++++●+++++●+++●+●+++++●+++●+++++●+++++++++++●+++++●+++

  ++●+++++++++++++●+++●+++++●+++++++++++●+++++++●+++++●++

  +●+++++++++++++++++++++++++●+++++++++++++++++●+++++++++

  ●+++++++●+++●+++++●+●+++++●+++++++++++++++++++++●++++++

  +++++●+●+++++++++++++++●+++++++●+++●+++++++++++●+++++++

  ++++++●+++++++++●+●+++●+++++++●+++++●+++++●+++●+●+++●++

  +++●+++++++●+++●+●+++++●+++++++++●+●+++++++++●+++++++●+

  ++●+++++++++++++●+++++++++●+++++++++++●+●+++++●+++●+●++

  +++++++++++++●+++++++++++++●+++●+++++●+++++++●+++++●+++

  ●+++++++++++++++++●+++++++●+++++++++●+++++●+++++●++++++

  +●+++++++++●+++++++++++●+++++++++++++●+++●+++++●+++++●+

Bei ungerader Zeilenbreite sind die Primzahlen unterschiedlich gut in beiden Diagonalrichtungen angeordnet.

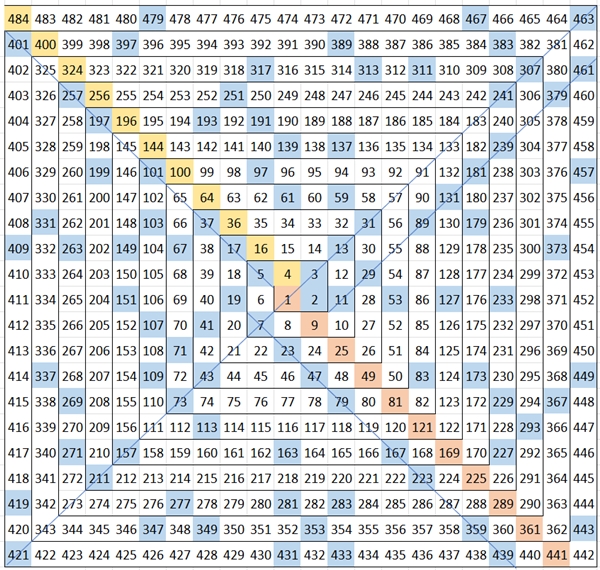
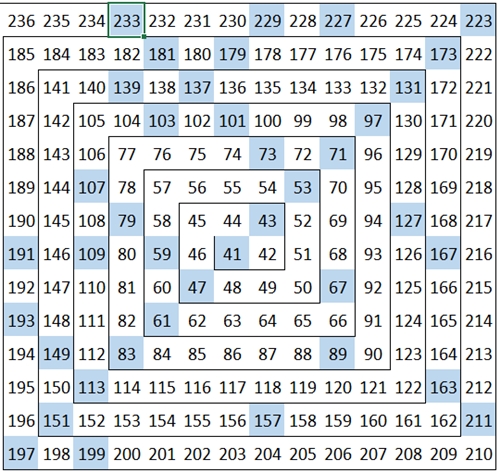
Bei der Ulam-Spirale werden die natürlichen Zahlen spiralförmig angeordnet:

Mit blauer Farbe sind die Primzahlen dargestellt, mit gelber Farbe die geraden Quadratzahlen und mit rosa Farbe die ungeraden Quadratzahlen.

Es gibt eine Vorzugsrichtung der Primzahlen in Diagonalrichtung, da sich die ungeraden Zahlen in Richtung der Diagonalen befinden und die Primzahlen mit Ausnahme der Zahl 2 ungerade Zahlen sind.

Die Zahlen der Halbdiagonale von 5 ausgehend nach links oben kann durch die Rekursion
a_n+1 = a_n + 4 + 8٠n mit a₀ = 1 und n = 0, 1, 2, 3, … berechnet werden.

Die Primzahlen auf der von links unten nach rechts oben verlaufenden Diagonalen werden durch die Formel
n² – n + 1 für n von 2 bis 23 erfasst:
3, 7, 13, 21, 31, 43, 57, 73, 91, 111, 133, 157, 183, 211, 241, 273, 307, 343, 381, 421, 463,
die durchgestrichenen Zahlen sind keine Primzahlen; sie kommen in der Diagonalen ebenfalls vor.

Startet man statt mit 1 mit der Zahl 41, so liefert die Formel n² – n + 41 für n von 1 bis 40 Primzahlen, die in der Diagonalen von links unten nach rechts oben auftauchen:

41, 43, 47, 53, 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281, 313, 347, 383, 421, 461, 503, 547, 593, 641, 691, 743, 797, 853, 911, 971, 1033, 1097, 1163, 1231, 1301, 1373, 1447, 1523, 1601,
n = 41 liefert  1681 = 41², n = 42 liefert 1763 = 41٠43, n = 43 liefert wieder eine Primzahl; es kommen anschließend Primzahlen und nicht Primzahlen vor.

Bereits Leonhard Euler (1707 – 1783)  hat mit der Formel n² + n +17 für n von 0 bis 15 Primzahlen erzeugt.

Es wird vermutet, dass es unendlich viele Primzahlzwillinge gibt, das sind Primzahlen, die die Differenz 2  haben.

Andererseits kann der Abstand zwischen zwei aufeinanderfolgenden Primzahlen beliebig groß werden.

Wie zufällig ist nun die Anzahl der Primzahlen pro Zeile im „Zahlenteppich“ mit einer vorgegebenen Zeilenbreite?

Weiterführende Internetseiten:

Ulam-Spirale – Wikipedia

http://de.wikipedia.org/wiki/Primzahlzwilling