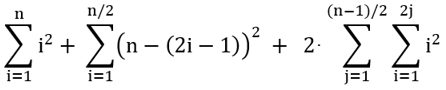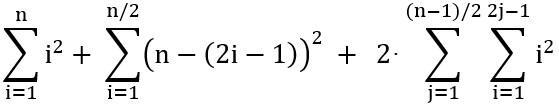Herleitung einer Formel für die Anzahl von Quadraten im Quadratgitter

Es wird dabei vorausgesetzt, dass die Eckpunkte der Quadrate auf Schnittpunkten des Quadratgitters liegen.

Kennzeichnung von Quadraten im Quadratgitter:

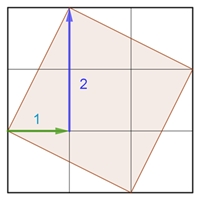
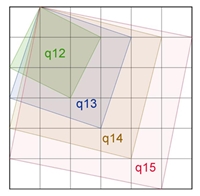
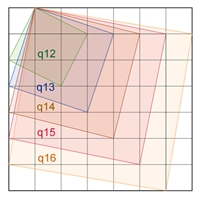
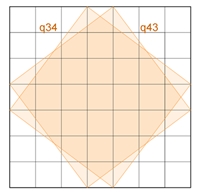
   q12 bedeutet: Quadrat in der links dargestellten Lage

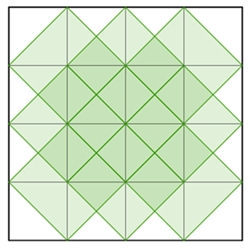
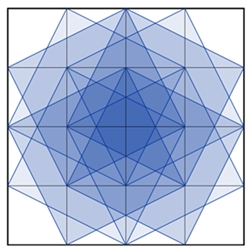
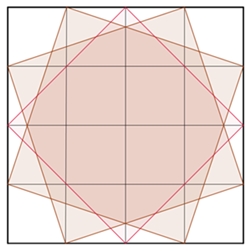
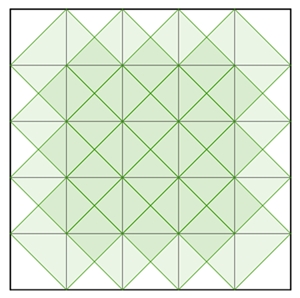
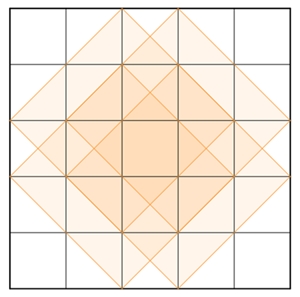
Darstellung der Quadrate, deren Eckpunkte auf Gitterpunkten eines Quadratgitters n*n liegen, und deren Seiten parallel zu den Gitterlinien verlaufen.

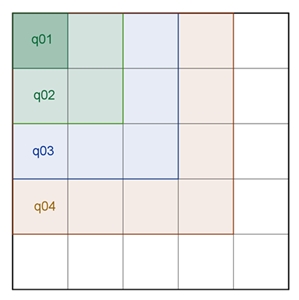
5*5-Quadratgitter:

25 q01 + 16 q02 + 9 q03 + 4 q04 + 1  = 55

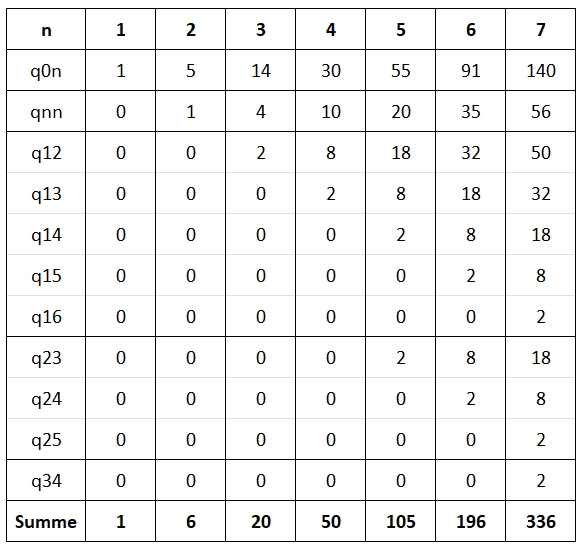
Anzahl der Quadrate q0n längs der Gitterlinien in einem Quadratgitter n*n für n von 1 bis 7:

1, 5, 14, 30, 55, 91, 140

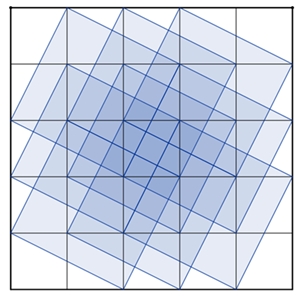
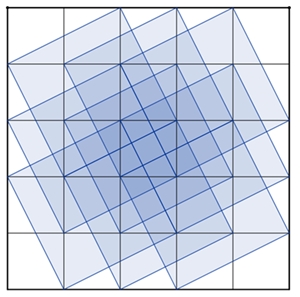
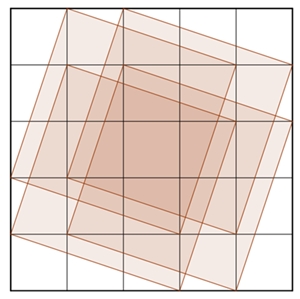
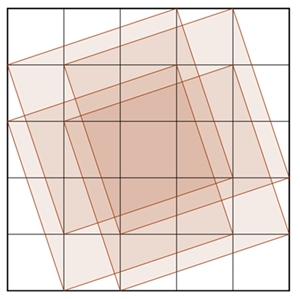
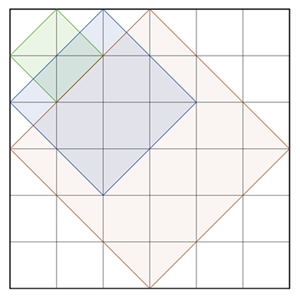
Darstellung der Quadrate, deren Eckpunkte auf Gitterpunkten eines Quadratgitters n*n liegen, und deren Seiten nicht parallel zu den Gitterlinien verlaufen.

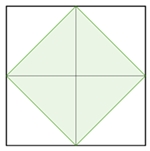
   1 Quadrat im Quadratgitter 2*2

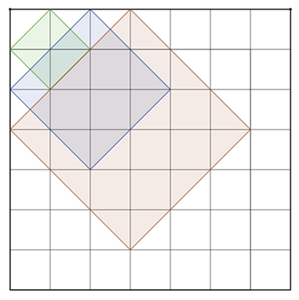
  Anzahl der Quadrate im Quadratgitter 3*3:

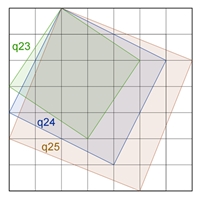
  4 q11 + 1 q12 + 1 q21 = 6

Anzahl der Quadrate im Quadratgitter 4*4

          9 q11        +     4 q12 + 4 q21  +  1 q13 + 1 q31 + 1 q22   =   20

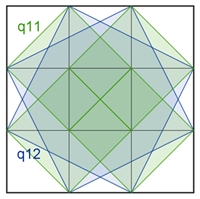
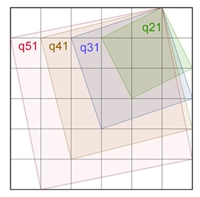
Anzahl der Quadrate im Quadratgitter 5*5

            16 q11              +               9 q12            +            9 q21              +               4 q13             +             4 q31          +            4 q22          +        1q14+1q41 +1q23+1q32  = 50

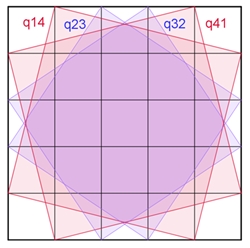
Anzahl der Quadrate im Quadratgitter 6*6

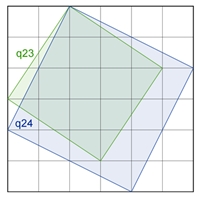
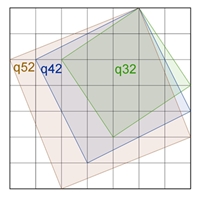
 25 q11 + 9 q22 + 1 q33 + (16 q12 + 9 q13 + 4 q14 + 1 q15) ⸱ 2     +     (4 q23  +  1 q24) ⸱ 2     =   105

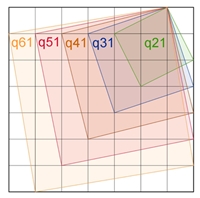
Anzahl der Quadrate im Quadratgitter 7*7

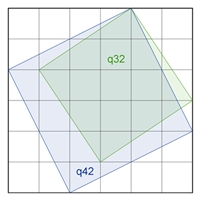
36 q11 + 16 q22 + 4 q33  + (25 q12 + 16 q13 + 9 q14 + 4 q15 + 1 q16) ⸱ 2    +     (9 q23 + 4 q24 + 1 q25) ⸱ 2         +          1 q34 + 1 q43   =  196

Anzahl der hier dargestellten Quadrate qxy (x ≠y) im Quadratgitter n*n für n von 1 bis 7:

0, 1,  6,  20, 50, 105, 196

Anzahl der Quadrate q0n längs der Gitterlinien in einem Quadratgitter n*n für n von 1 bis 7:

1, 5, 14, 30, 55, 91, 140

Anzahl der Quadrate in einem Quadratgitter n*n für n von 1 bis 7 insgesamt:

1, 6, 20, 50, 105, 196, 336

Tabelle für die Anzahl der Quadrate im Quadratgitter n*n in Abhängigkeit von qxy

Formel für die Gesamtzahl der Quadrate eines Quadratgitters n*n:

Für n gerade:

Für n ungerade:

Die Anzahl der Quadrate in einem Quadratgitter n*n lässt sich auch mit Hilfe folgender Polynomfunktion darstellen:

f(x) = 1/12 x⁴ + 1/3 x³ + 5/12 x² + 1/6 x