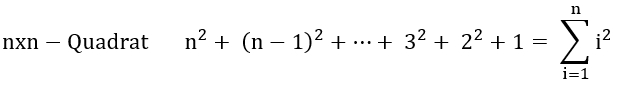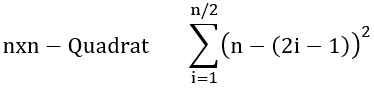|
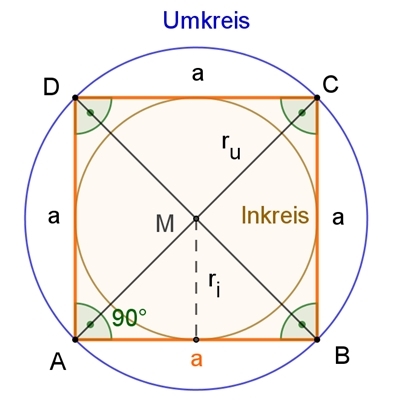
Das Quadrat
Umfang u = 4 a Inkreisradius ri =Umkreisradius
ru
=
Innenwinkel
α = β = 𝛾 = δ = 90°
Diagonallänge
d =
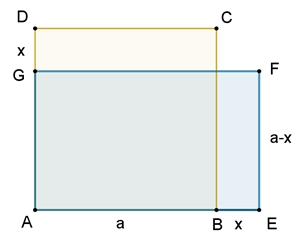
Das Quadrat hat unter den Rechtecken mit gleichem Umfang den größten Flächeninhalt:
Umfang des Quadrats uQ
= 4a
Umfang des Rechtecks uR
= 2(a+x) + 2(a–x) = 4a
Flächeninhalt des Quadrats AQ
= a²
Flächeninhalt des Rechtecks AR
= (a+x)(a–x) = a² – x²
Daraus folgt:
AQ
> AR
für x > 0
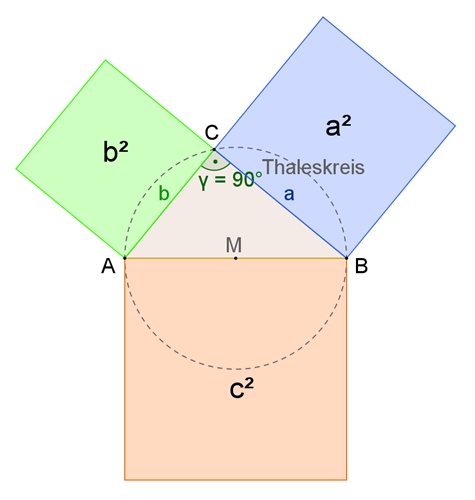
a² + b² = c²
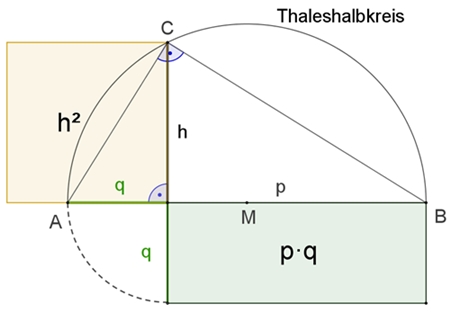
Die Quadratur des Rechtecks mit Hilfe des
Höhensatzes
Die eine Seite des Rechtecks sei der
Hypotenusenabschnitt p und die andere Seite der Hypotenusenabschnitt q eines
rechtwinkligen Dreiecks.
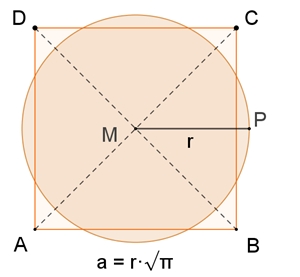
Die Quadratur des Kreises
Ein Quadrat mit dem gleichen Flächeninhalt eines
Kreises kann nicht konstruiert werden, da die Wurzel aus π nicht
konstruierbar ist.
Flächeninhalt des Kreises:
r2π
Flächeninhalt des Quadrats:
Quadratzahlen
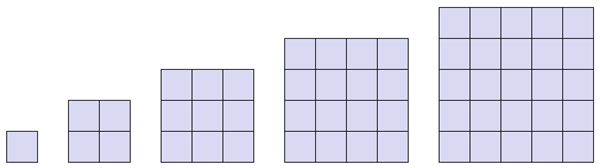
Wenn die Seitenlänge eines Quadrats n-fach so groß wird, wird die Fläche des
Quadrats n²-fach so groß
Entsprechend
gehören zu den natürlichen Zahlen 1, 2, 3, 4, 5, …, n die Quadratzahlen 1, 4,
9, 16, 25, …, n².
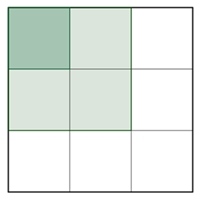
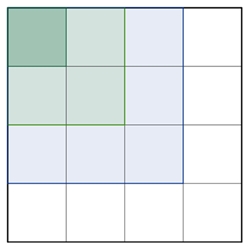
Anzahl der Quadrate eines Quadratgitters
a)
Anzahl der Quadrate längs der Gitterlinen
Quadrat-Typ
Anzahl der Quadrate
1x1
–
Quadrat
1
2x2
–
Quadrat 4 + 1 = 5
3x3
–
Quadrat
9 + 4 (2x2-Quadrate) + 1 = 14
4x4
–
Quadrat
16 + 9 (2x2-Quadrate) + 4 (3x3-Quadrate) + 1 = 30
5x5
–
Quadrat
25 + 16 (2x2-Quadrate) + 9 (3x3-Quadrate) + 4 (4x4-Quadrate) + 1 = 55 . . .
Für n = 2, 3, …, 11 erhält man als Anzahl von Quadraten: 1, 5, 14, 30, 55, 91, 140, 204, 285, 385
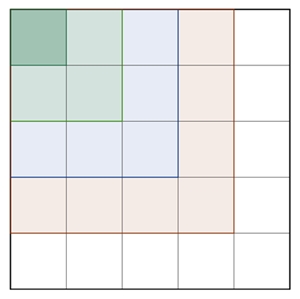
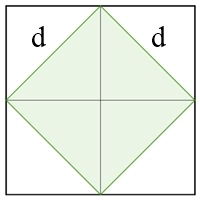
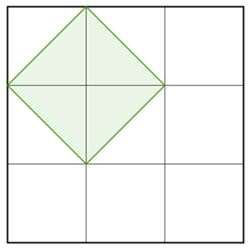
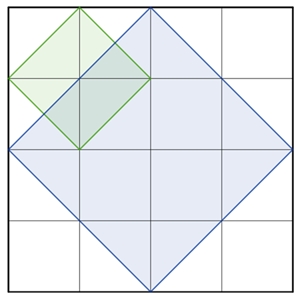
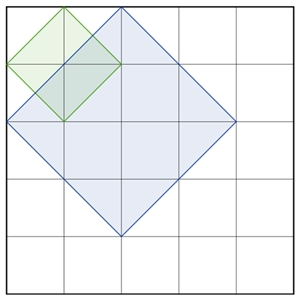
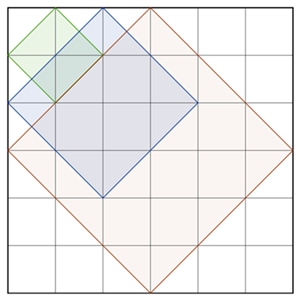
b) Anzahl der Quadrate längs der Diagonalen zu den Gitterlinien
Quadrat-Typ
Anzahl zusätzlicher schiefer Quadrate
2x2 – Quadrat
1
3x3 – Quadrat
4 (dxd-Quadrate)
4x4 – Quadrat
9 (dxd-Quadrate) + 1 (2dx2d-Quadrat) = 10
5x5 – Quadrat
16 (dxd-Quadrate) + 4 (2dx2d-Quadrate) = 20
6x6 – Quadrat
25 (dxd-Quadrate) + 9 (2dx2d-Quadrate) + 1 ((3dx3d-Quadrat) = 35 . . .
Für n = 1, 2, 3, …, 10 erhält man als Anzahl von Quadraten:
1, 4, 10, 20,
35, 56, 84, 120, 165, 220
c) Anzahl aller Quadrate in einem
Quadratgitter n*n:
→Lösung
Ein natürliches
(normales) magisches Quadrat der Ordnung (Kantenlänge) n ist eine
quadratische Anordnung der Zahlen 1, 2, 3, ..., n2,
wobei die Summen jeder Zeile, jeder Spalte und jeder der beiden Diagonalen
den gleichen Wert besitzen.
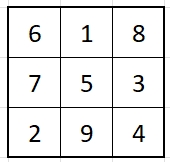
Magisches 3x3-Quadrat
Lateinische Quadrate
Ein lateinisches Quadrat ist ein quadratisches Schema mit n Reihen
und n Spalten, wobei jedes Feld mit einem von n verschiedenen Symbolen
belegt ist, so dass jedes Symbol in jeder Zeile und in jeder Spalte jeweils
genau einmal auftritt. Die natürliche Zahl n wird Ordnung des lateinischen
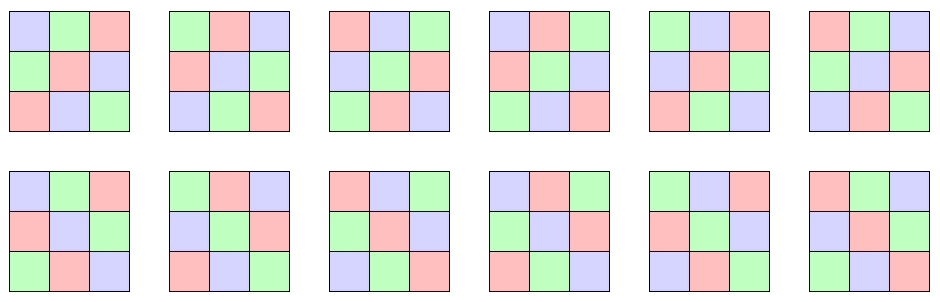
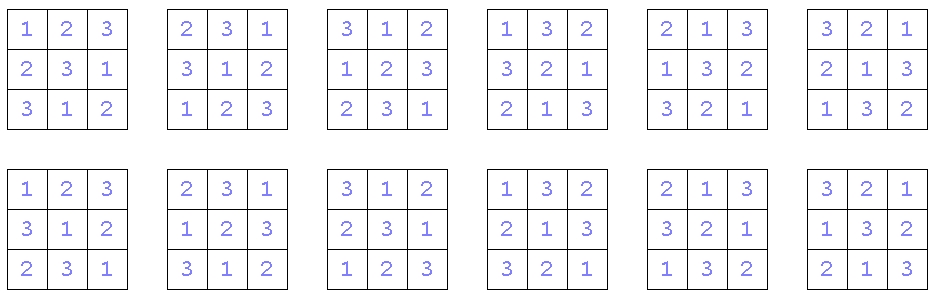
Quadrats genannt. Die 12 lateinische Quadrate der Ordnung 3, mit Farben und mit Zahlen:
Durch Spiegelungen, Drehungen um 90° und zyklische
Spaltenvertauschungen können aus einem lateinischen Quadrat der Ordnung 3
alle anderen erzeugt werden.
Anzahl der verschiedenen lateinische Quadrate der Ordnung n = 1, 2, 3, 4, 5,
6, 7, … :
3-Quadrat:
3!٠2!
= 12
4-Quadrat:
4!٠3!٠2²
= 576
5-Quadrat:
5!٠4!٠23٠7
=
161280
6-Quadrat:
6!٠5!٠26·3·72
= 812851200
7-Quadrat:
7!٠6!٠210·3·5·1103
=
61479419904000 Es ist kein Bildungsgesetz für die Zahlenfolge
bekannt. Ein lateinisches
Quadrat der Ordnung 9 mit der Zusatzbedingung, dass in der Aufteilung in 9
3×3-Quadrate in jedem dieser Quadrate alle Ziffern von 1 bis 9 jeweils genau
einmal auftreten, führt zu dem Zahlenrätsel
Sudoku.
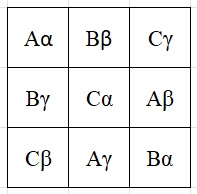
Griechisch-lateinische Quadrate Ein griechisch-lateinisches Quadrat (GLQ) oder Eulersches Quadrat der Größe n ist ein quadratisches Schema mit n Zeilen und n Spalten, bei dem in jedem der der n⸱n Felder ein Zeichen aus einer Menge L und eines aus einer anderen Menge G eingetragen ist. Dabei muss in jeder Zeile und auch in jeder Spalte jedes Element aus L und ebenso jedes Element aus G genau einmal stehen und jedes lateinisch-griechische Paar darf nur einmal vorkommen.
Der Mathematiker Leonhard Euler nannte diese Felder
griechisch-lateinische Quadrate, da er Buchstaben aus dem griechischen und
lateinischen Alphabet für die Werte verwendete.
Es wird auch als orthogonales lateinisches
Quadrat bezeichnet.
L = {A, B, C}, G = {α, β, γ}
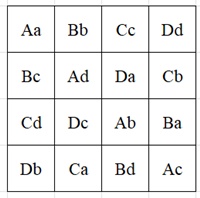
GLQ 4x4
L = {A, B, C, D}, G = {a, b, c, d}
GLQ 5x5
Die Parkettierung der Ebene nur mit gleich großen Quadraten
Quadrate in archimedischen Parkettierungen
Die
Quadratur von Quadraten
Unter der Quadratur von Quadraten versteht man eine Parkettierung eines
gegebenen Quadrats mit kleineren Quadraten, deren Seitenlängen ganzzahlige
Werte haben.
Eine perfekte Quadratur von Quadraten ist eine Quadrat-Parkettierung, die
keine kongruenten Teilquadrate enthält.
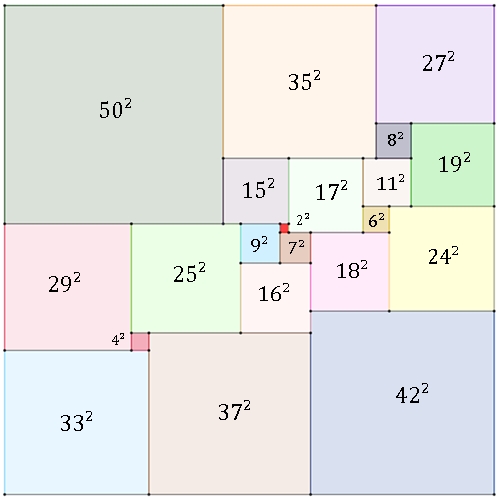
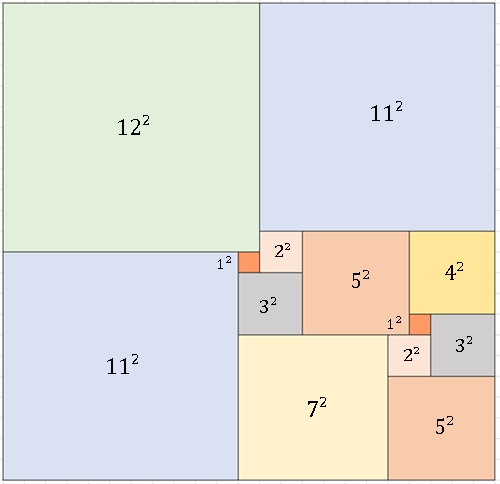
Kleinstmögliche perfekte Quadratur der Ordnung 21;
A. J. W. Duijvestijn fand 1978 mit Computerhilfe die perfekte Quadratur der Ordnung 21 und bewies, dass dies die geringstmögliche Ordnung und zugleich die einzige dieser Ordnung ist.
Eine unperfekte Quadratur von
Quadraten ist eine Quadrat-Parkettierung, die mehrere kongruente Teilquadrate enthält.
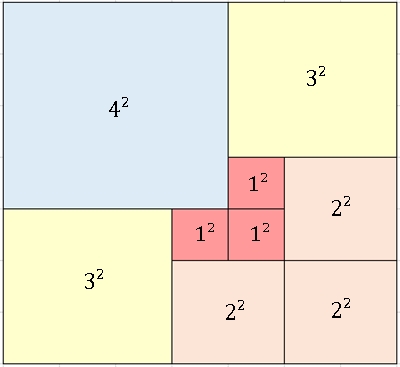
Kleinstmögliche unperfekte Quadratur der Ordnung 13 mit höchstens zwei
kongruenten Teilquadraten;
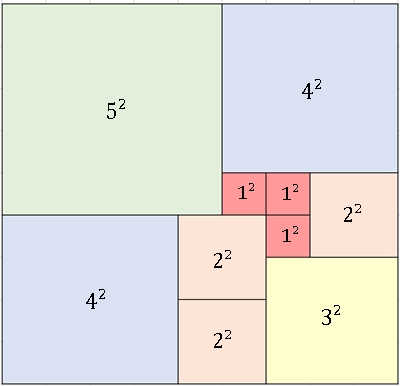
Unperfekte Quadratur der Ordnungen 9 und 10 mit höchstens drei kongruenten
Teilquadraten
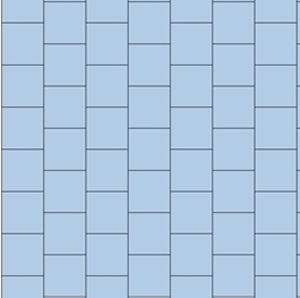
Optische Täuschung mit Quadraten
Die grauen Linien sind tatsächlich parallel
(Café-Wand-Illusion, entdeckt 1898 durch A. H. Pierce, USA).
Wenn man die schwarzen Quadrate hellgrau
färbt, sieht man die grauen Linien als Parallelen.
Die linken Linien des Schachbrettmusers sind parallel, wie das rechte
Bild zeigt. Die kleinen Quadrate bewirken die optische Täuschung.
Diese und die untere optische Täuschung (ohne Animation) hat der japanische Psychologieprofessor
Akiyoshi
Kitaoka auf
Akiyoshi's illusion pages
Durch die dunklen und hellen kleinen Kreuze scheinen sich im Quadratmuster Wellen zu bilden; dies ist bei einfarbigen Kreuzen nicht der Fall.
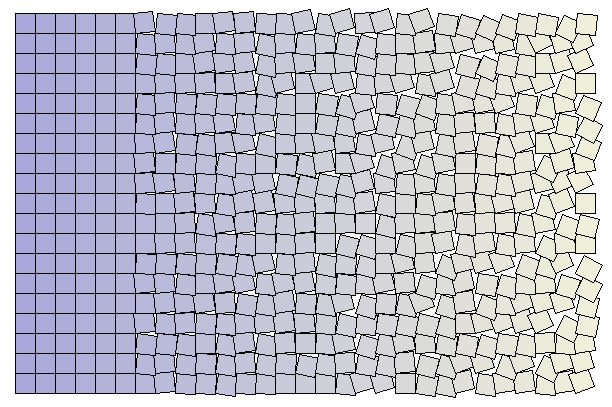
Quadrate, von der Ordnung zur Unordnung Mosaik-Quadrate
Die Bilder wurden mit geogebra dargestellt oder mit Python programmiert. Zurück Zurück zur Startseite |