Das Heptagramm – der siebenzackige Stern

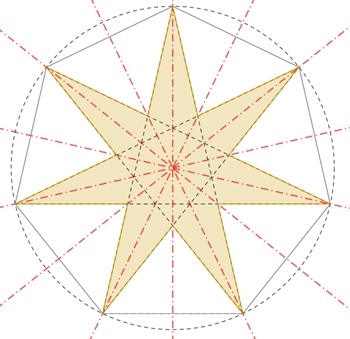
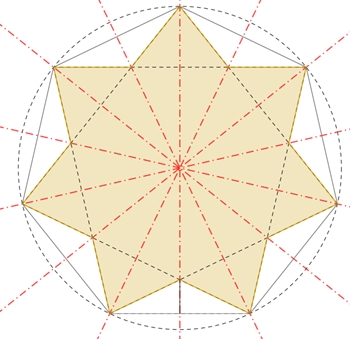
Das Heptagramm ist ein siebenzackiger Stern, dessen Eckpunkte die Eckpunkte eines regulären Siebenecks sind. Es besitzt 7 Symmetrieachsen. Es gibt zwei unterschiedliche Formen:
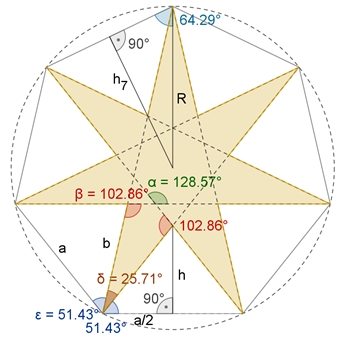
{7/3}-Heptagramm und {2/2}- Heptagramm.

{7/3}-Heptagramm

Winkelberechnungen

α = 5·180°/7 = 900°/7 ≈ 128,57°

β‘ = 180° – 2 α‘ = 180° – 2 (180° – α) = 2 α – 180° = 1800°/7 – 180° = 540°/7

β = 180° – β‘ = 720°/7 ≈ 102,86°

δ = 360° – (α + 2 β) = 360° – (900°/7 + 1440°/7) = 180°/7 ≈ 25,71°

2 ε + δ = α

ε = (α – δ)/2 = 360°/7 ≈ 51,43°

Berechnung von b und R in Abhängigkeit von der Seitenlänge a des regulären Siebenecks:

cos(360°/7) = a/2 / b

b = a / (2 cos(360°/7))

b ≈ 0,802 a

cos(α /2) = a/2 / R

R = a / (2 cos(α /2))

R ≈ 1,152 a

Der Umfang u des {7/3}-Heptagramms beträgt u = 14 b ≈ 11,23 a

Flächeninhalt A des {7/3}- Heptagramms ist gleich dem Flächeninhalt des regulären Siebenecks mit Seitenlänge a minus 7 Dreiecksflächen A_△ mit der Seitenlänge a und der Höhe h.

Flächeninhalt A₇ des regulären Siebenecks mit Seitenlänge a:
A₇ = 7·1/2·a h₇         NR: h₇² = R² – (a /2)²  (Pythagoras)
                                         h₇² ≈ 1,328 a² – 1/4 a² = 1,078 a²
                                         h₇ ≈ 1,038 a

A₇ ≈ 3,5·1,038 a² = 3,63 a²

A_△ = 1/2·a·h                NR: h² = b² – (a/2)²  (Pythagoras)

                                             h² ≈ 0,393 a²

                                             h ≈ 0,627 a

A_△ ≈  0,313 a²

A =  A₇  – 7 A_△ ≈ 3,63 a² – 7·0,313 a² = 1,44 a²

Flächeninhalt A des {7/3}-Heptagramms beträgt A ≈ 1,44 a²

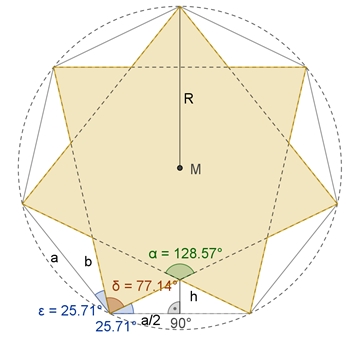
{7/2}-Heptagramm