Neunzackiger Stern

Die Eckpunkte eines neunzackigen Sterns sind die Eckpunkte eines regulären Neunecks. Er besitzt 9 Symmetrieachsen. Es gibt drei unterschiedliche Formen:
{9/4}-{9/3}-{9/2}-Stern

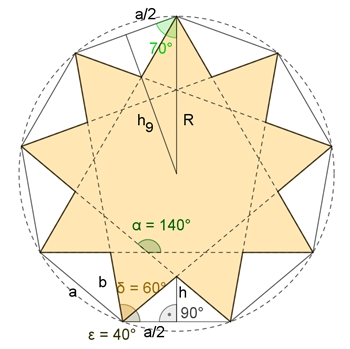
{9/3}-Stern

Winkelberechnungen

α = 7·180°/9 = 140°  (Innenwinkel im regulären Neuneck)

2 ε + δ = α

ε = (α – δ)/2 = 40°

Berechnung von b und R in Abhängigkeit von der Seitenlänge a des regulären Neunecks:

cos(40°) = a/2 / b

b = a / (2 cos(40°))

b ≈ 0,653 a

Der Umfang u des {9/3}-Sterns beträgt u = 18 b ≈ 11,75 a

cos(70°) = a/2 / R

R = a / (2 cos(70°))

R ≈ 1,46 a

Der Flächeninhalt A des {9/3}- Sterns ist gleich dem Flächeninhalt A₉ des regulären Neunecks mit Seitenlänge a minus 9 Dreiecksflächen A_△ mit der Seitenlänge a und der Höhe h.

Flächeninhalt A₉ des regulären Neunecks mit Seitenlänge a:
A₉ = 9·1/2·a h₉         NR: h₉² = R² – (a/2)²  (Pythagoras)
                                         h₉² ≈ 2,137 a² – 0,25 a² = 1,887 a²
                                         h₉ ≈ 1,374 a

A₉ ≈  6,181 a²

A_△ = 1/2·a·h                NR: h² = b² – (a/2)²   (Pythagoras)

                                             h² ≈ 0,176 a²

                                             h ≈ 0,42 a

A_△ ≈  0,21 a²

A =  A₉  – 9 A_△ ≈  6,181 a² – 9·0,21 a² ≈ 4,29 a²

Flächeninhalt A des {9/3}-Sterns beträgt A ≈ 4,29 a²

Bemerkung:

In der Bahai-Religion gilt der neunzackige Stern als Symbol für Vollkommenheit und Einheit.

Zurück

Zurück zur Themenseite
Zurück zur Startseite