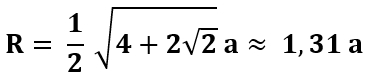Das Oktogramm – der Achtstern

Das Oktogramm ist ein achtzackiger Stern, dessen Eckpunkte die Eckpunkte eines regulären Achtecks sind. Es besitzt 8 Symmetrieachsen. Es gibt zwei unterschiedliche Formen:
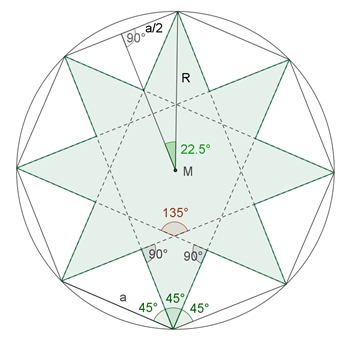
{8/3}-Oktogramm und {8/2}-Oktogramm.

{8/3}-Oktogramm

Berechnung von b und R in Abhängigkeit von der Seitenlänge a des regulären Achtecks:

b² + b² = a² (Pythagoras)

b = √2/2 a

Der Umfang u des {8/3}-Oktogramms beträgt u = 16 b = 8√2 a

sin(22,5°) = a/2 / R  (Sinussatz)

R = a / (2 sin(22,5°)

Flächeninhalt A des {8/3}-Oktogramms ist gleich dem Flächeninhalt des regulären Achtecks mit Seitenlänge a minus 4 Quadrate der Seitenlänge b.

Flächeninhalt A₈ des regulären Achtecks mit Seitenlänge a:
A₈ = 8·1/2·a h         NR: h² = R² – (a  /2)² (Pythagoras)
                                       h² = 1/4 ( 4 + 2√2) a² – 1/4 a² = 1/4 (3 + 2√2) a²

A₈ = 2 √(3 + 2√2) a² = (2 + 2√2) a²             Begr.: 4 (3 + 2√2) = (2 + 2√2)²

                                                                                 12 + 8√2 = 4 + 8√2 + 8

A = (2 + 2√2) a² – 4 ·1/2 a² =  2√2 a²

Flächeninhalt A des {8/3}-Oktogramms beträgt A = 2√2 a² ≈ 2,83 a²

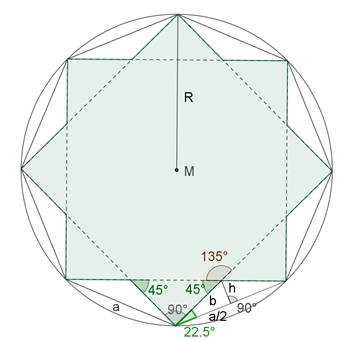
{8/2}-Oktogramm

cos(22,5°) = a/2 / b

b = a /(2 cos(22,5°)

b = 1/2 √(4 – 2√2) a

Der Umfang u des {8/2}-Oktogramms beträgt u = 16 b:

Flächeninhalt A des {8/2}-Oktogramms ist gleich dem Flächeninhalt des regulären Achtecks A₈ mit Seitenlänge a minus 8 Dreiecksflächen A_△ mit der Seitenlänge a und der Höhe h.

A_△ = 1/2·a·h                      NR: h² + (a/2)² = b²

                                                   h² =  1/4 (4 – 2√2) a² – 1/4 a² = 1/4 (3 – 2√2)

                                                   h = 1/2 √(3 – 2√2)

 A_△ = 1/4 √(3 – 2√2) a² = 1/4 (√2 – 1) a²

Flächeninhalt A des {8/2}-Oktogramms: 

A =  A₈ – 8 A_△ = (2 + 2√2) a² – 2 (√2 – 1) a²

A = 4 a²