|
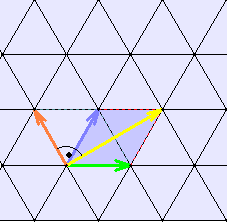
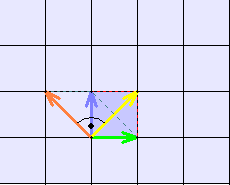
Parkette mit regelmäßigen Vielecken und spiralförmige Parkette 1) Platonische oder reguläre Parkettierungen, halbreguläre Parkettierungen Eine Parkettierung der Ebene besteht aus einer Menge von Parkettsteinen oder Grundmustern, die die Ebene ohne Überlappungen und ohne Lücken bedeckt. Als Grundmuster werden hier nur regelmäßige Vielecke betrachtet. Platonische oder reguläre Parkettierungen, die genau ein Grundmuster benötigen, entstehen nur durch das gleichseitige Dreieck, Quadrat oder regelmäßige Sechseck. Parkettstein: gleichseitiges Dreieck Quadrat reguläres Sechseck
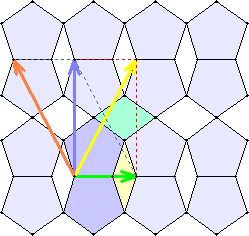
Durch schrittweise Verschiebung des Grundmusters in Richtung oder Gegenrichtung des grünen oder blauen Pfeils entsteht die reguläre Parkettierung.
Der grüne und
blaue Pfeil sind Repräsentanten zweier linear unabhängiger Vektoren
Durch
Linearkombination von
Die
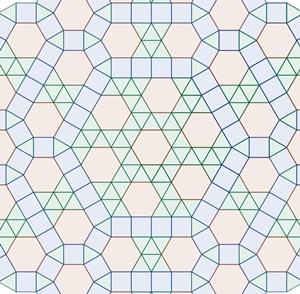
Linearkombination Halbreguläre Parkettierungen entstehen bei Verwendung von mehr als einem Grundmuster. Beispiele:
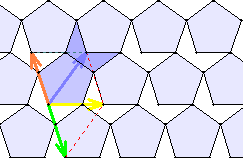
Zwei verschiedene Grundmuster: Regelmäßiges Fünfeck und konkaves Fünfeck mit gleich langen Seiten. Der orange Pfeil ist hier der Gegenpfeil zum grünen Pfeil.
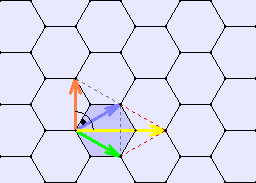
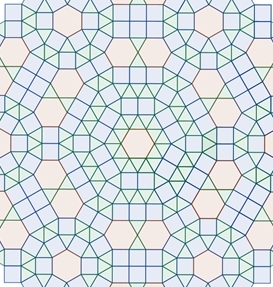
Drei verschiedene Grundmuster:
Zwei symmetrische
regelmäßige Fünfecke und zwei verschiedene Rauten.
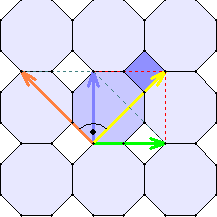
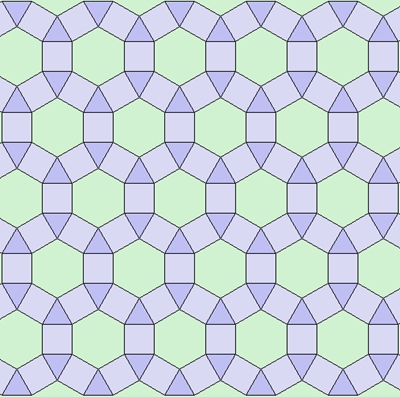
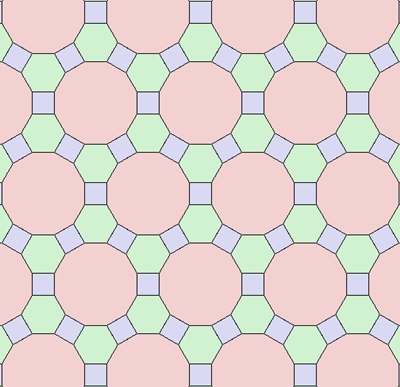
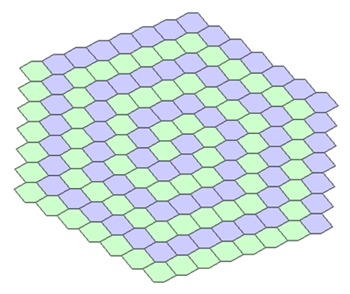
Zwei verschiedene Grundmuster: Ein regelmäßiges Achteck und ein Quadrat. (archimedische Parkettierung)
Die Verschiebungseigenschaften sind die gleichen wie bei der regulären Parkettierung. 2) Archimedische Parkette
Parkette, in denen zwei
oder drei verschiedene regelmäßige n-Ecke mit gleich langen Seiten vorkommen
und deren Ecken gleichartig aufgebaut sind, d.h. in denen die regelmäßigen
n-Ecke in gleicher Anzahl und Reihenfolge aneinander stoßen, heißen
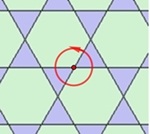
archimedische Parkettierungen. Kennzeichnung über eine Parkettecke: Bei einer Drehung um einen Eckpunkt wird der Reihe nach die Eckenzahl der Vielecke angegeben, z.B.
Auf ein Dreieck folgt ein Sechseck, dann wieder ein Dreieck und ein Sechseck.
Die 8 verschiedenen archimedischen
Parkettierungen
Die platonischen und archimedischen
Parkettierungen werden homogene Parkettierungen genannt.
3)
Semireguläre und weitere nicht homogene Parkettierungen
Werden als
Grundform beliebige regelmäßige Drei-, Vier- und Sechs-Ecke mit
gleicher Kantenlänge verwendet, so ergeben sich ohne Einschränkung bei der
archimedischen Parkettierung - dass an jedem Punkt, an dem die Ecken
zusammenstoßen, immer die gleiche Kombination der drei Vielecke
zusammenstoßen müssen - weitere mögliche Parkettierungen.
Parkettierungen,
für die zwar als Grundform beliebige regelmäßige Vielecke mit gleicher
Kantenlänge verwendet werden, bei denen aber an den Punkten, an denen die
Ecken der Vielecke zusammenstoßen, eine von zwei möglichen Kombinationen von
Vielecken auftritt, nennt man semireguläre oder 2-uniforme
Parkettierungen.
Beispiele:
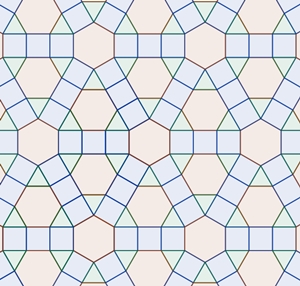
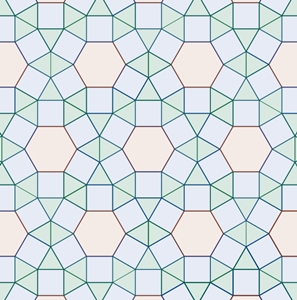
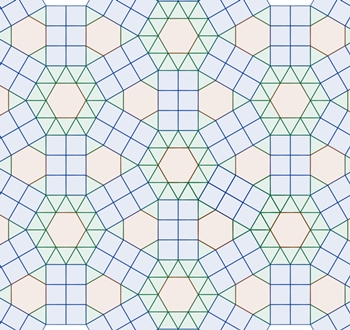
3-4-6-4, 3-4-4-6 3-4-6-4, 3-3-4-3-4 3-4-4-6, 3-6-3-6
Weder homogene noch
semireguläre Parkettierungen
Beispiele:
3-3-3-3-6, 3-3-4-3-4, 3-3-3-4-4, 3-3-3-3-6, 3-3-3-4-4, 3-3-3-3-6, 3-3-3-4-4, 3-3-4-3-4,
3-4-4-6, 4-4-4-4
3-3-4-3-4, 3-4-4-6, 3-4-6-4
3-4-4-6, 3-4-6-4,
3-6-3-6
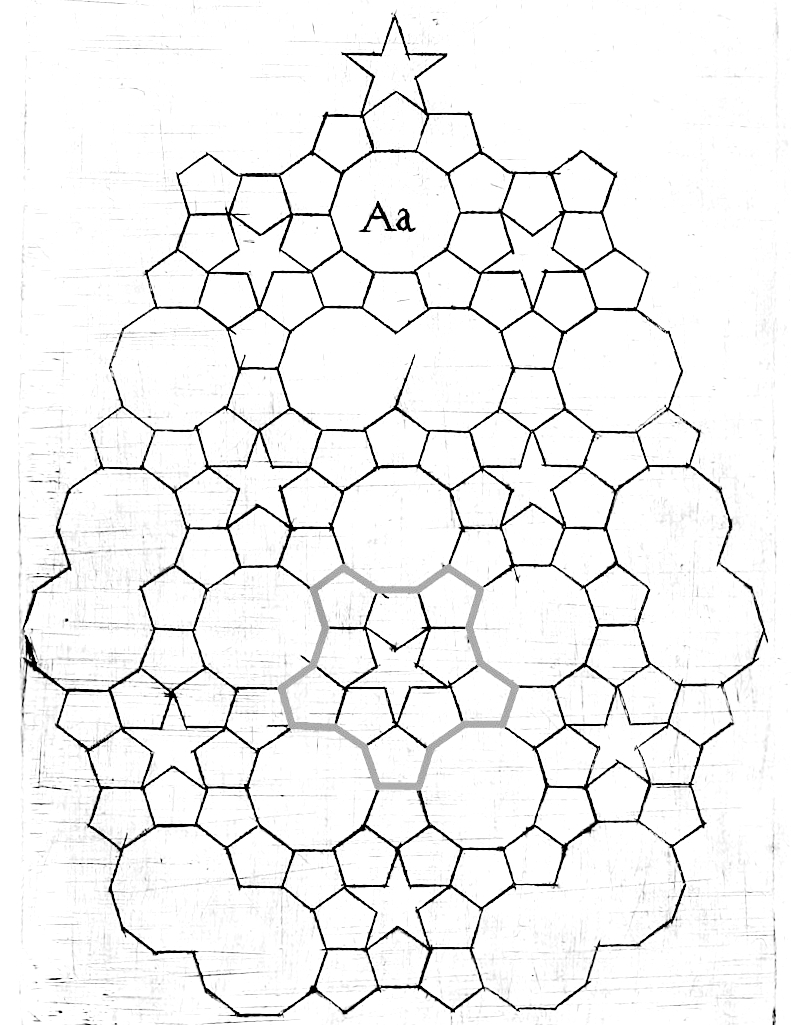
4) Kepler-Parkett
Johannes Kepler (1571 – 1630) hat sich auch mit Parkettierungen mit Fünfecken beschäftigt. Er wusste, dass man mit Fünfecken allein die Ebene nicht parkettieren kann. Von ihm stammt nebenstehende Figur. (s. Parkette bei Johannes Kepler)
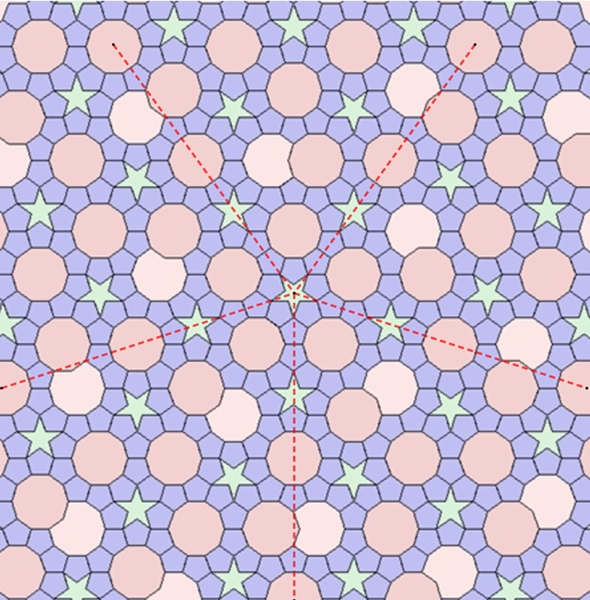
Wenn man neben Pentagramm (Fünfstern), regulärem Fünfeck und regulärem
Zehneck auch ein sonst reguläres Zehneck mit einem konkaven Eckteil zulässt,
lässt sich die Ebene parkettieren. Das Parkett hat dann eine 5fache Rotationssymmetrie
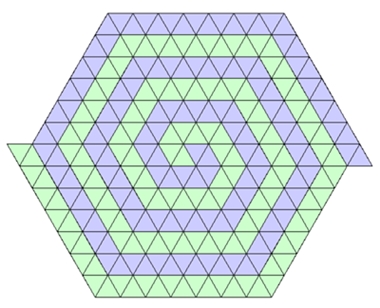
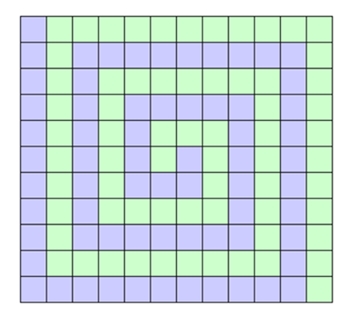
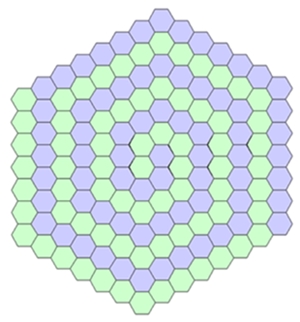
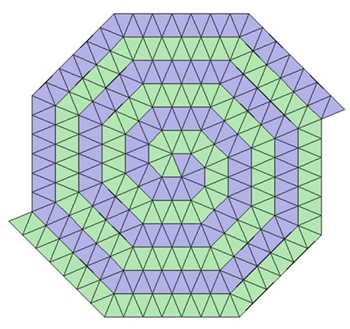
5) Zweifache spiralförmige Parkette (Spiralparkette)
Mit dem regulären Dreieck, Viereck und Sechseck als Parkettstein lassen sich
auch spiralförmige Parkette erzeugen.
Diese sind nicht-periodisch und besitzen auch keine Achsensymmetrie. Bei
Vernachlässigung der Farbgebung besitzen sie jedoch eine Rotationssymmetrie
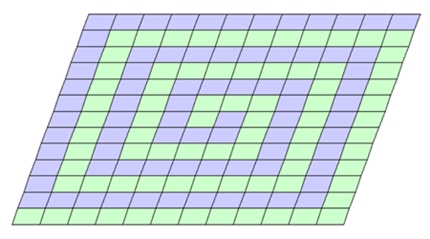
Die Scherung
der Parkettsteine liefert wieder spiralförmige Parkette, z.B.:
Die Parkettsteine sind dann beliebige Dreiecke, beliebige Parallelogramme
und Sechsecke mit jeweils gleich langen gegenüberliegenden Seiten
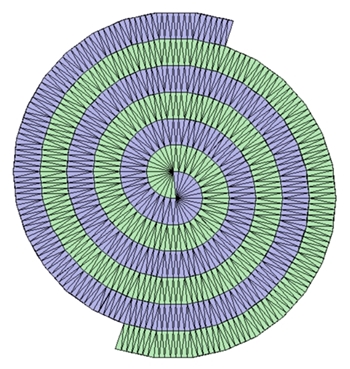
Wenn man als Parkettsteine gleichschenklig spitzwinklige Dreiecke verwendet
nähert sich die Spiralform bei zunehmend spitzerem Winkel immer besser der
Archimedischen
Spirale an. Spitze Winkel:
45°
30°
12°
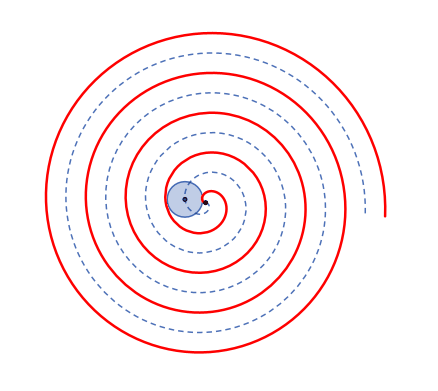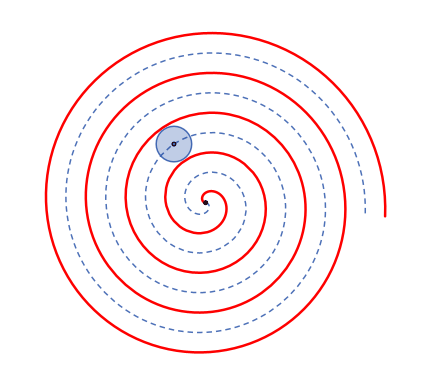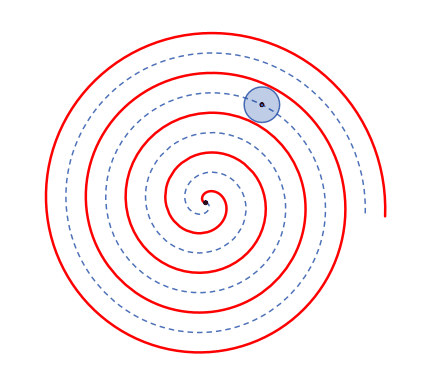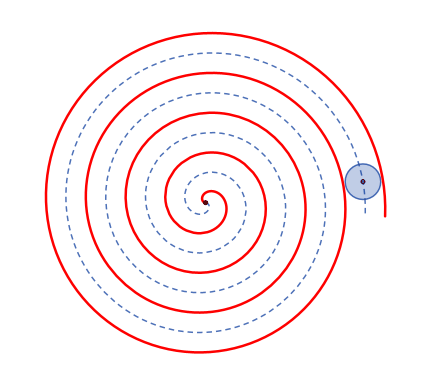
Überlagerung von
Kreisevolvente (rot)
Bei der
Kreisevolvente ist der
Abstand
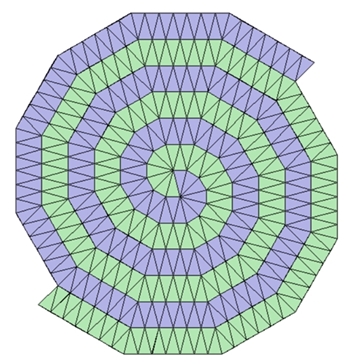
6) Einfache spiralförmige Parkette (Spiralparkette)
Mit dem
gleichseitigen konkaven Fünfeck, Siebeneck und Neuneck als Parkettsteine lassen
sich einfache spiralförmige Parkette erzeugen.
Parkettstein:
Fünfeck
Siebeneck
Neuneck
Die grünen 3-5-7-Ecke sind in Spiralrichtung
linksgedreht, die blauen 3-5-7-Ecke rechtsgedreht.
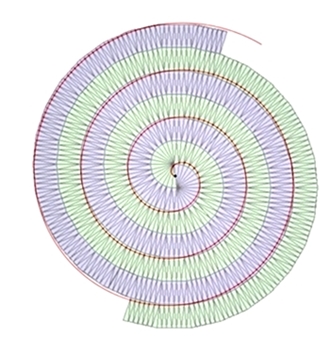
Überlagerung von Kreisevolvente (rot) und Neuneck-Spirale:
Eine Siebzehneck-Spirale etwas farbiger:
7) Parkettähnliche mehrfache Spiralen 3fache, 5fache und 7fache Spirale mit sich
überdeckenden Kreisen
Zurück Zurück zur Startseite |