Parkette bei Johannes Kepler

Johannes Kepler (Weil der Stadt 27.12.1571  – 15.11.1630 Regensburg) war Mathematiker, Physiker, Astronom, Astrologe und Naturphilosoph. Er verfasste 1619 in lateinischer Sprache das Werk Harmonices Mundi Libri V (5 Bücher zur Harmonie der Welt), in dem er auch das dritte Keplersche Gesetz veröffentlichte.

Im 2. Buch über die Kongruenz harmonischer Figuren enthält das Werk Abhandlungen zur Geometrie, unter anderem zur Parkettierung der Ebene mit regulären Vielecken. Kepler verwendet für Parkettierung das Wort Kongruenz und fortsetzbar.

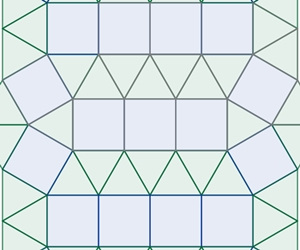
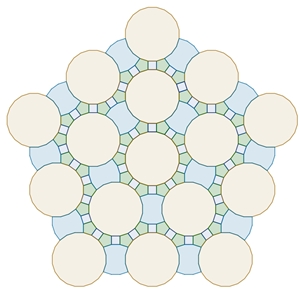
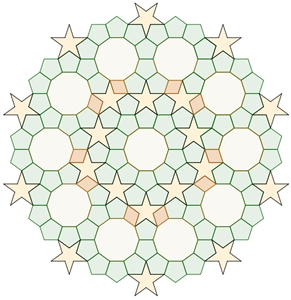
Im Buch enthalten sind Konstruktionen seiner Parkettierungen oder Parkettierungsversuche, die im Folgenden zu sehen sind. Die einzelnen Figuren sind mit Buchstaben bezeichnet.

Blatt 1                                                                           Blatt 2

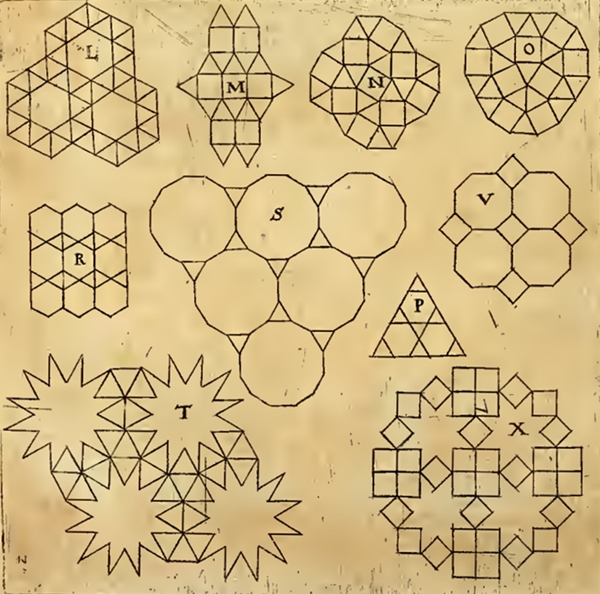
Bei den meisten Konstruktionen bzw. Zeichnungen ist die Art der Parkettierung klar. Es gibt aber auch Beispiele wie die Figuren M, N und O in Blatt 2, wo es mehrere Möglichkeiten einer Parkettierung gibt.

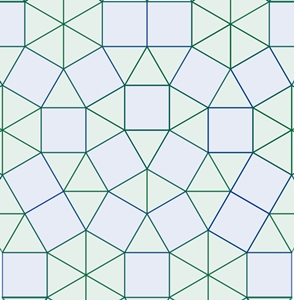
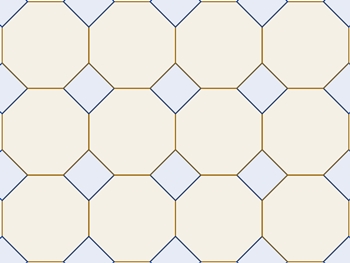
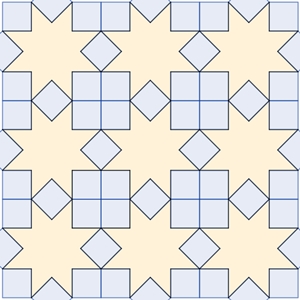
Folgende Konstruktionen wurden für eine Parkettierung nach den Vorlagen von Kepler in Blatt 1 und 2 durchgeführt.

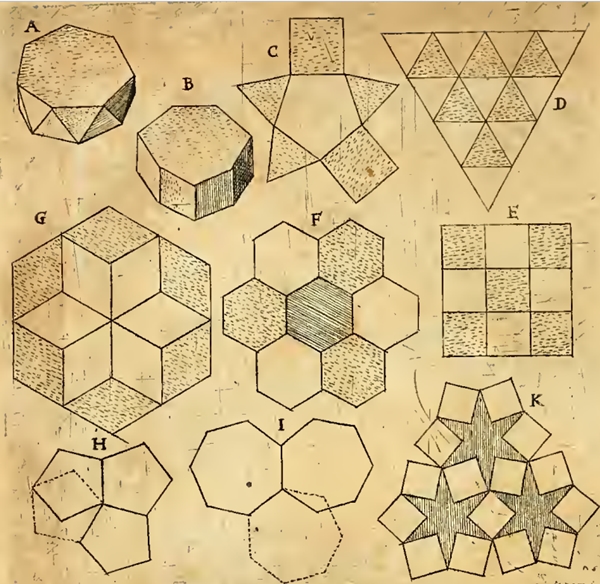
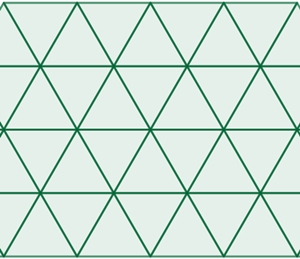
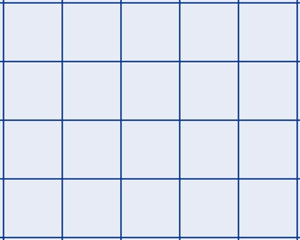
Die Figuren D, E und F sind einfache Parkettierungen mit nur einem regulären Polygon (Vieleck) als Parkettstein, u.z. mit gleichseitigem Dreieck, Quadrat und regulärem Sechseck. Es gibt nur diese drei sogenannten platonischen Parkettierungen, was auch Kepler erkannte.

Bei den weiteren Parketten sind 6 der 8 archimedischen Parkettierungen enthalten.

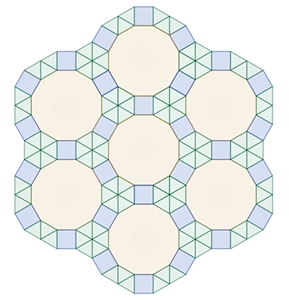
   Die Figur K hat als Parkettsteine ein Quadrat und einen regulären Sechseckstern.

Die Figuren M, N und O haben jeweils 2 verschiedene Parkettsteine als Bausteine für eine Parkettierung,
u. z. gleichseitiges Dreieck und Quadrat.

Die Figuren L, P und R haben auch jeweils 2 verschiedene Parkettsteine als Bausteine für eine Parkettierung,
u. z. gleichseitiges Dreieck und reguläres Sechseck.

Die Figuren S, V, T und X haben auch jeweils zwei unterschiedliche Parkettsteine für eine Parkettierung, kurz:
Figur S: 3-12-Eck, Figur V: 4-8-Eck, Figur T: 3eck-12eckstern, Figur X: 4eck-8eckstern

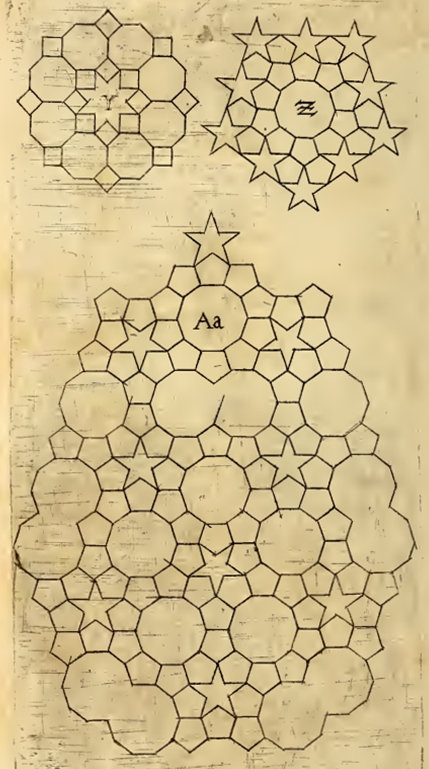
Die Figur Y hat drei verschiedene Parkettsteine,
u.z. Quadrat, reguläres Achteck und regulären Achteckstern.

Blatt 3                                                          Blatt 4                                                               Blatt 5 (Teil)

Folgende Konstruktionen wurden für eine Parkettierung nach den Vorlagen von Kepler in Blatt 3, 4 und 5 (Teil) durchgeführt.

Die Figur Aa besteht aus regulären Fünfecken, regulärem Fünfeckstern, regulärem Zehneck und einem eingedrückten Zehneck, das zur Parkettierung benötigt wird. Kepler schreibt dazu in seinem Werk:

Structura est laborisissima et artificiosissima visenda ad eandem literam Aa.
(Die Struktur ist sehr beschwerlich und sehr kunstvoll, zu sehen bei denselben Buchstaben Aa.)

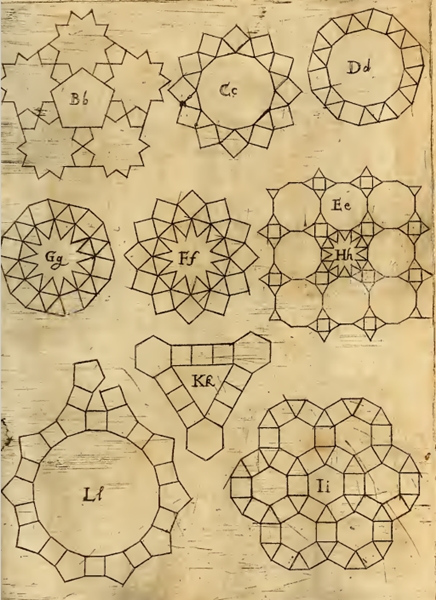
Die Figur Bb besteht aus zwei unterschiedlich großen regulären Fünfecken und einem regulärem Zehneckstern. Mit Hilfe eines eingedrückten Zehnecksterns lässt sich die Figur fortsetzen, ähnlich wie bei Figur Aa. Dies wusste auch Kepler.

Die Figuren Cc und Dd haben als Parkettsteine ein gleichseitiges Zwölfeck, ein Quadrat und ein gleichseitiges Dreieck. Diese können Vorlage für eine Parkettierung sein. Für Kepler sind die Figuren Cc und Dd nicht forsetzbar.

Figur Gg entspricht Figur Dd mit einem regulären Zwölfeckstern und 12 gleichseitigen Dreiecken im Zwölfeck, Figur Ff entspricht Figur Cc mit einem regulären Zwölfeckstern und 12 gleichseitigen Dreiecken im Zwölfeck. Mit den Figuren H, I, Z und Ll kann es keine Parkettierung geben.

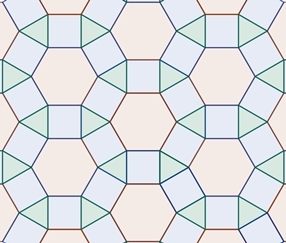
Die Figuren Ee und Hh mit regulärem Zwölfeck, gleichseitigem Dreieck und Quadrat dienen ohne und mit regulärem Zwölfeckstern als Parkettsteine für eine Parkettierung.

Die Figuren Kk und Ii lassen sich mit gleichseitigem Dreieck, Quadrat und regulärem Sechseck als Parkettsteine zu einem Parkett fortsetzen.

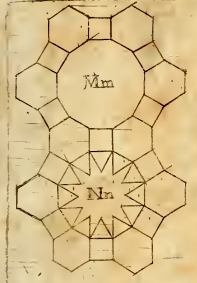
Die Figuren Mm und Nn haben drei bzw. vier unterschiedliche Parkettsteine, kurz:
Figur Mm: 4-6-12-Eck, Figur Nn: 3-4-6-Eck-12eckstern.

Die Figur Y hat drei verschiedene Parkettsteine, u.z. Quadrat, reguläres Achteck und regulären Achteckstern.

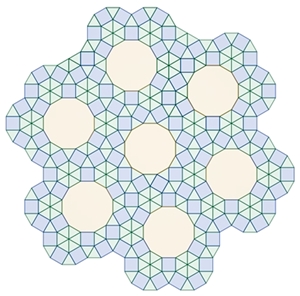
Mögliche Parkettierung von Figur Ll mit Hilfe eines doppelt eingedrückten Zwölfecks, vorgegebene Parkettsteine sind Quadrat, reguläres Fünfeck und reguläres Zwanzigeck.

Mögliche Parkettierung von Figur Z mit Hilfe einer Raute, vorgegebene Parkettsteine sind reguläres Fünfeck, reguläres Zehneck und regulärer Fünfeckstern.

Bemerkung:

Während es die Kunst der Mosaike schon seit Jahrtausenden gibt, hat das Studium der Mosaike in der Mathematik erst in der Neuzeit begonnen.

Johannes Kepler war einer der ersten Mathematiker, der Studien über Parkettierungen mit regelmäßigen Vielecken (regelmäßigen Polygonen) durchführte.

Kepler argumentiert bei fortsetzbaren Formen von einem gemeinsamen Eckpunkt der angrenzenden regelmäßige Polygone aus. Die Summe der Eckwinkel der angrenzenden Polygone muss 4 Rechte (360°) ergeben. Dann ergibt sich keine Lücke. Dies untersucht er für Formen, die aus einzelnen oder mehreren regelmäßigen Polygonen bestehen.

Er spricht von Kongruenz in der Ebene, wenn die einzelnen Ecken mehrerer regelmäßiger Figuren so in einem Punkt zusammenstoßen, dass keine Lücke übrigbleibt.

Die Kongruenz heißt vollkommen, wenn die zusammenstoßenden Ecken jeder regelmäßigen Figur alle in derselben Art zusammenstoßen, so dass also die Anordnung der Ecken in jedem Punkt die gleiche ist und sich ins Unendliche fortsetzen lässt.

Er spricht von vollkommenster Kongruenz, wenn die zusammenstoßenden regelmäßigen Figuren in der Ebene von gleicher Art sind (das ist bei der platonischen Parkettierung der Fall).

Auch heute werden die Parkette über die Eckpunkte klassifiziert (s. Klassifizierung von Parketten).

Quelle:

Harmonices Mundi Libri V