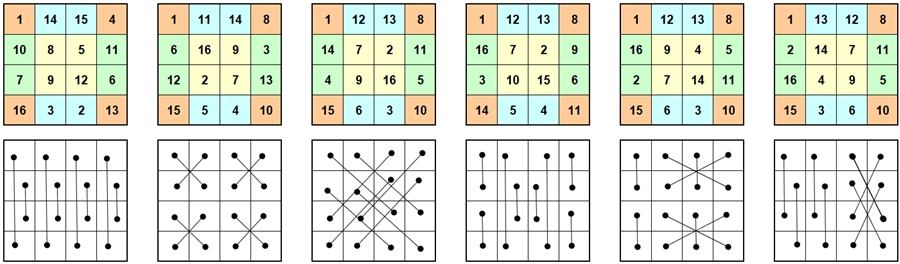
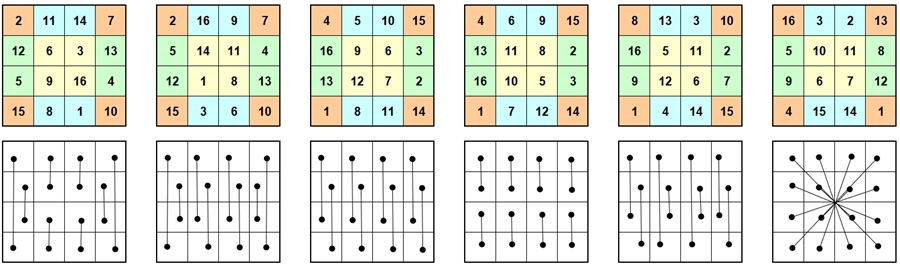
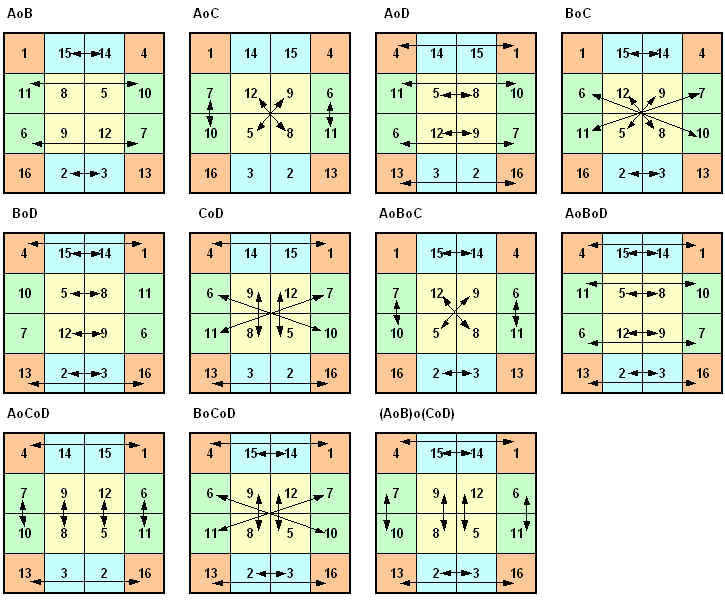
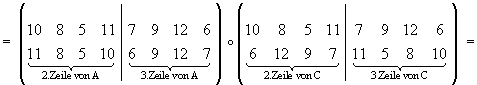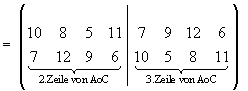Magische Quadrate der Ordnung 4 und Gruppeneigenschaften

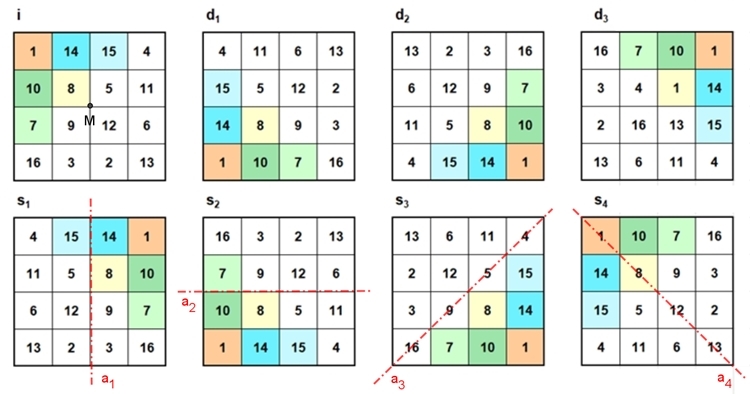
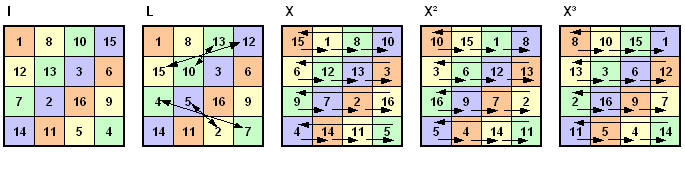
Ein natürliches magisches Quadrat der Ordnung 4 mit den natürlichen Zahlen von 1 bis 16 besitzt 880 Grundformen und 7 mal 880 weitere Darstellungsformen, die durch Spiegelungen und Drehungen aus den Grundformen hervorgehen. Das heißt, es gibt insgesamt 7040 verschiedene Darstellungsformen. Auf jede der 880 Grundformen können die Abbildungen der Diedergruppe D₄ angewandt werden.
Die Zeilen-, Spalten- bzw. Diagonal-Summen des magischen 4x4-Quadrats ergeben jeweils 34.

Mag_4x4-Quadrat

Im magischen 4x4-Quadrat liefern die Zahlen in den gleichfarbigen, symmetrisch liegenden Zellen ebenfalls die Summe 34.

1. Gruppeneigenschaften bei magischen Quadraten

a) Die Diedergruppe D₄ der Ordnung 8.

Ein bestimmtes magisches Quadrat der Ordnung 4 wird als Grundform gewählt und 7 weitere Darstellungsformen entstehen durch Spiegelungen und Drehungen aus der Grundform.

Bezeichnungen:

d_1,2,3 : Drehung um 90°, 180°, 270° gegen den Uhrzeigersinn mit Drehzentrum M (Quadratmitte)

i = d₄ : identische Abbildung = Drehung um 360° gegen den Uhrzeigersinn mit Drehzentrum M.

s_1,2,3,4 : Spiegelung an der Achse a₁, a₂, a₃, a₄.

Mag_4*4-Quadrat-D4

D₄ = { i,d₁, d₂, d₃, s₁, s₂, s₃, s₄} bildet die Diedergruppe D₄ der Ordnung 8 mit der Verknüpfungstafel (Gruppentafel) siehe: Magisches 3x3-Quadrat.

b) Die Gruppen G₈ und G₁₆ der Ordnungen 8 und 16

Die verschiedenen Grundformen besitzen teilweise ebenfalls Gruppeneigenschaften bezüglich der Abbildungen, die die Grundformen ineinander überführen.
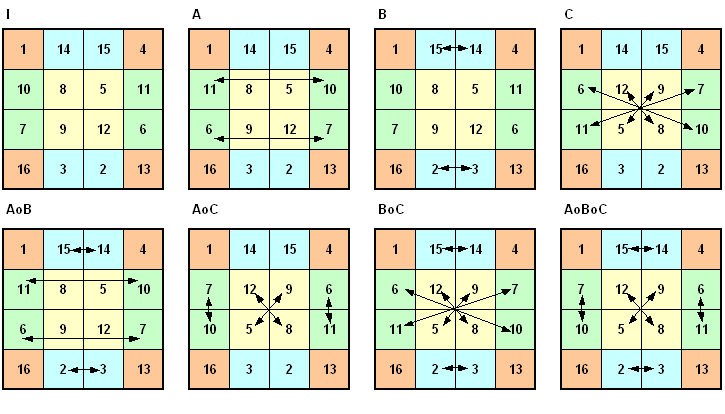
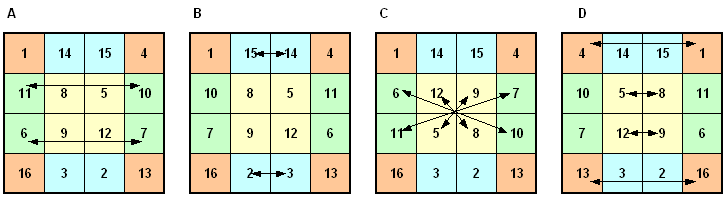
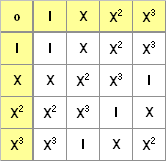
Zunächst wird eine spezielle Untergruppe von Abbildungen der Ordnung 8 bei magischen Quadraten dargestellt, bei der die Eckwerte 1, 4, 13, 16 (im Uhrzeigersinn) fest bleiben.

Bezeichnungen:

I : identische Abbildung (mit vorgegebener Grundform)

A, B, C : vorgegebene elementare Abbildungen (s.u.)

o : Verknüpfung (Hintereinanderausführung) zweier Abbildungen von links nach rechts

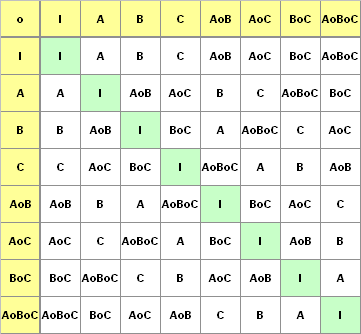
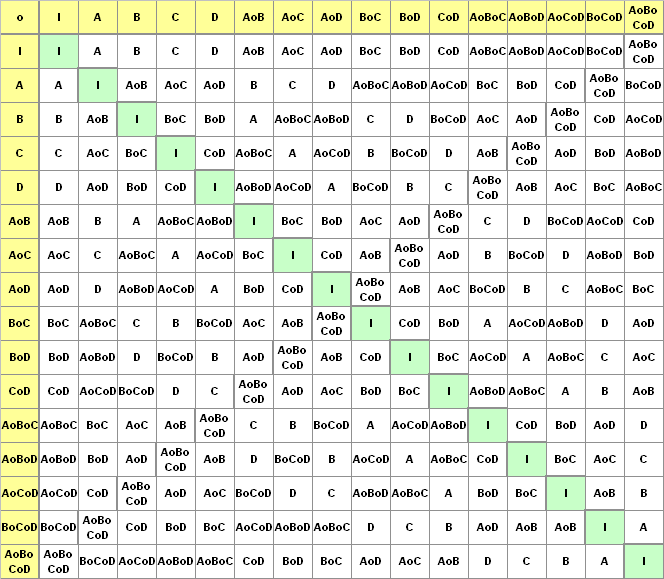
G₈ = { I, A, B, C, AoB, AoC, BoC, AoBoC } bildet eine Untergruppe der Ordnung 8. Die Untergruppe wird von den elementaren Abbildungen A, B und C erzeugt. Die Quadrate bleiben dabei magische Quadrate.

Folgende Verknüpfungstafel stellt eine Gruppentafel dar, wobei die 1. Abbildung in der linken Spalte steht:

Bemerkungen:

Die Untergruppe der Ordnung 8 ist ähnlich strukturiert wie die Diedergruppe der Ordnung 8 .

Es gibt hier jedoch keine zyklische Untergruppe, d.h. es fehlen als Abbildungen die Drehungen.
Die Gruppentafel ist symmetrisch bezüglich der Diagonalen durch I aufgebaut.
Dies ist begründet durch die Gültigkeit des Kommutativ- und Assoziativgesetzes.

Durch Hinzunahme der elementaren Abbildung D entsteht eine Untergruppe mit 16 Elementen.

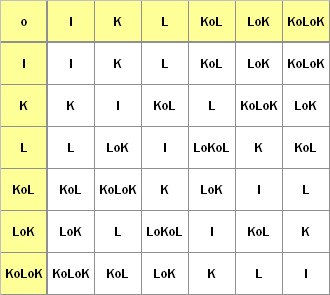
G₁₆ = { I, A, B, C, D, AoB, AoC, AoD, BoC, BoD, CoD, AoBoC, AoBoD, AoCoD, BoCoD, AoBoCoD } bildet eine Untergruppe der Ordnung 16. Die Untergruppe wird von den elementaren Abbildungen A, B, C und D erzeugt und besitzt 6 Zweifachverknüpfungen, 4 Dreifachverknüpfungen und eine Vierfachverknüpfung.

Folgende Verknüpfungstafel stellt die zugehörige, zur Diagonalen durch I symmetrische Gruppentafel dar:

Bemerkung:

Die Gruppe G₈ ist eine Untergruppe von G₁₆ .

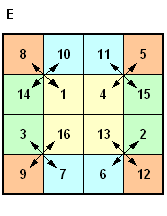
Durch Hinzunahme der elementaren Abbildung E entsteht eine Gruppe G₃₂der Ordnung 32, in der die vorhergehenden Gruppen als Untergruppen enthalten sind. Die Gruppe G₃₂ wird von 5 elementaren Abbildungen erzeugt und besitzt neben der identischen Abbildung 10 Zweifachverknüpfungen, 10 Dreifachverknüpfungen, 5 Vierfachverknüpfungen und eine Fünffachverknüpfung. Die Quadrate bleiben dabei symmetrische magische Quadrate.

Bemerkungen:

Die aufgeführten Abbildungsgruppen erfassen nur einen kleinen Teil aller Abbildungsgruppen.

Durch die Hinzunahme weiterer elementarer Abbildungen können die Abbildungsgruppen erweitert werden.
Die Verknüpfung zweier Abbildungen muss nicht wieder ein magisches Quadrat ergeben. Es kann auch ein eingeschränkt magisches Quadrat, z.B. halbmagisches Quadrat, entstehen.

Mit Hilfe der Matrizenschreibweise lassen sich Abbildungen leichter verknüpfen. Falls die erste und vierte Zeile des magischen Quadrats bei der Verknüpfung keine Rolle spielen, z.B.

A o C

2. Gruppeneigenschaften bei pandiagonalen magischen Quadraten

Es gibt insgesamt 48 verschiedene Grundformen von pandiagonalen magischen (panmagischen) Quadraten.

Werden die Grundformen mit Hilfe der Diedergruppe D₄ gespiegelt und gedreht, entstehen insgesamt 48 * 8 = 384 verschiedene Darstellungsformen pandiagonaler magischer Quadrate. Die folgenden pandiagonalen magischen Quadrate sind außerdem symmetrisch und vollkommen perfekt.

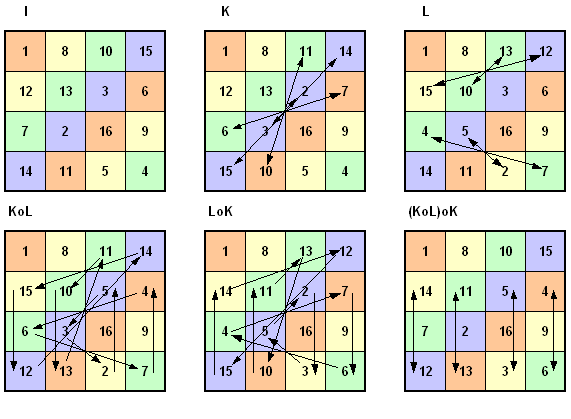
Bezeichnungen:

I : identische Abbildung (vorgegebene Grundform: pandiagonales magisches Quadrat)

K, L : vorgegebene elementare Abbildungen (s.u.)

o : Verknüpfung (Hintereinanderausführung) zweier Abbildungen

Folgende nicht-kommutative Gruppe H₆ der Ordnung 6 ist eine Untergruppe der Abbildungsgruppe, die alle 384 Formen erzeugt.
H₆ = { I, K, L, KoL, LoK, KoLoK }

Es gilt: KoLoK = LoKoL

(KoL)² = (KoL)o(KoL) = (KoLoK)oL = (LoKoL)oL = (LoK)o(LoL) = LoK
(LoK)² = (LoK)o(LoK) = KoL

Zugehörige nicht-kommutative Gruppentafel:

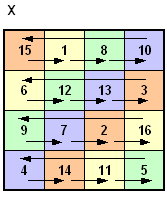
Folgende zyklische Gruppe Z₄ = { X, X², X³, X⁴ = I } der Ordnung 4 ist eine Untergruppe der Abbildungsgruppe, die alle 48 verschiedenen Grundformen erzeugt.

Erzeugende Abbildung X: Zugehörige Gruppentafel mit X²= XoX, usw.: