Rhombendodekaeder und Rhombentriakontaeder

Es gilt der Polyedersatz von L. Euler (1707 – 1783): e + f = k + 2
e = Anzahl der Ecken, f = Anzahl der Flächen, k = Anzahl der Kanten

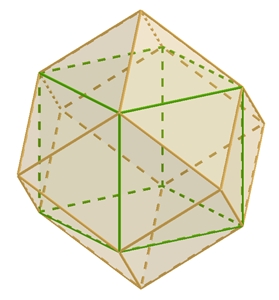
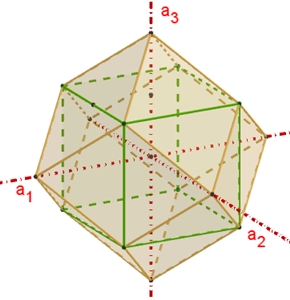
Das Rhombendodekaeder

Das Rhombendodekaeder ist ein Polyeder mit 12 Rauten (Rhomben), 14 Ecken und 24 Kanten. An sechs der Ecken grenzen vier Kanten und an die übrigen acht Ecken grenzen drei Kanten. Nach Polyedersatz von Euler: 12 + 14 = 24 + 2.

Das Rhombendodekaeder entsteht durch Aufsetzen einer Pyramide auf die quadratischen Seitenflächen eines Würfels.

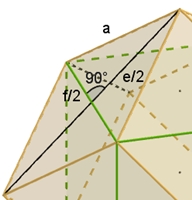
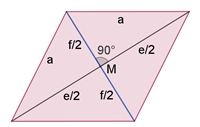
Die Würfelkanten bilden die Diagonale f der Raute mit der Seitenlänge a.

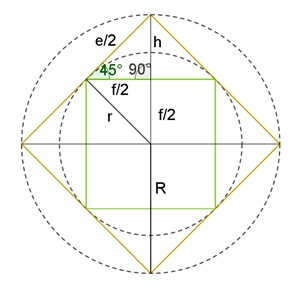
Querschnitt durch das Rhombendodekaeder

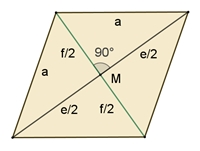
Nur wenn die Höhe h der Pyramide gleich der halben Würfelkante ist (h = f/2), schneiden die Verbindungsstrecken benachbarter Pyramidenspitzen die Würfelkanten senkrecht. Dadurch entsteht eine ebene Raute mit den Diagonalen e und f.

(e/2)² = (f/2)² + (f/2)²   (Pythagoras)

e = f √2

 f und e in Abhängigkeit von a:
f²/4 + e²/4 = a² (Pythagoras)
f²/4 + f²/2 = a²

f² = 4/3 a²
f  = 2/3 √3 a  und  e = 2/3 √6 a

Flächeninhalt A_R der Raute in Abhängigkeit von a:

A_R = e·f / 2 = √2/2 f² 

A_R = 2/3 √2 a²

Oberflächeninhalt A des Rhombendodekaeders: A = 12 A_R = 8√2 a² ≈ 11,314 a²

Berechnung des Volumeninhalts V des Rhombendodekaeders:

Volumeninhalt V_P einer aufgesetzten Pyramide:

V_P = 1/3 f² h = 1/6 f³  (Pythagoras)

V = f³ + 6·V_P  = 2 f³

V = 2 (2/3 √3 a)³

Volumeninhalt V des Rhombendodekaeders: V = 16/9 √3 a³ ≈ 3,079 a³  

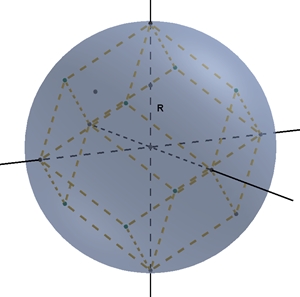
Radius R der Umkugel durch die Pyramidenspitzen des Rhombendodekaeders: R = f = 2/3 √3 a ≈ 1,155 a

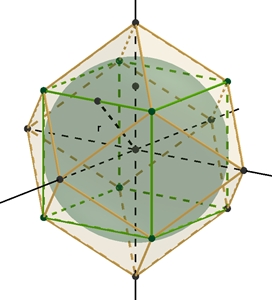
Radius r der Inkugel des Rhombendodekaeders: r = 1/3 √6 a ≈ 0,816 a

r² = f²/4 + f²/4 = f²/2
r = √2/2 f = 1/3 √6 a

Rhombendodekaeder mit Umkugel und mit Inkugel

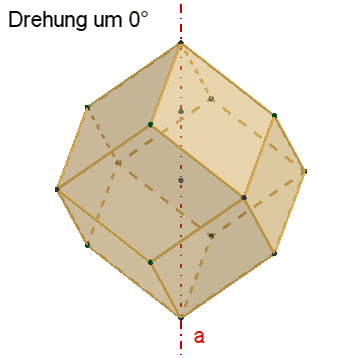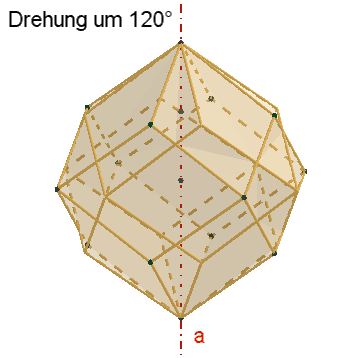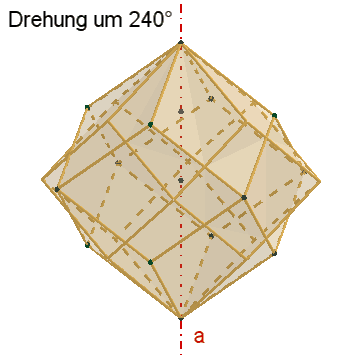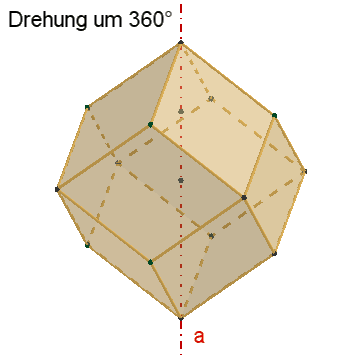
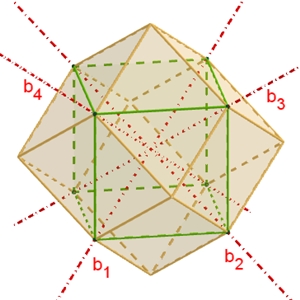
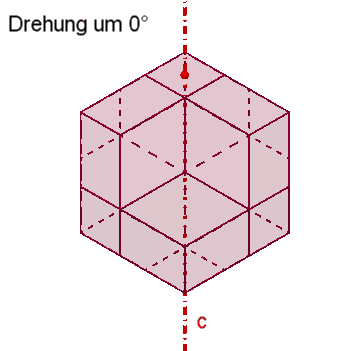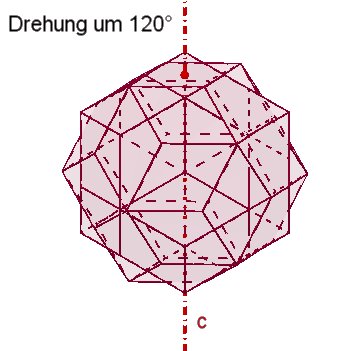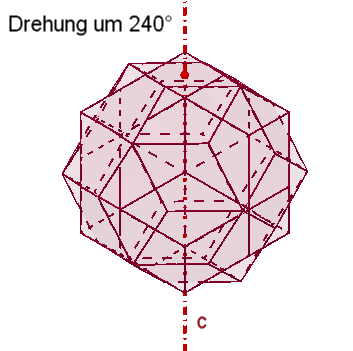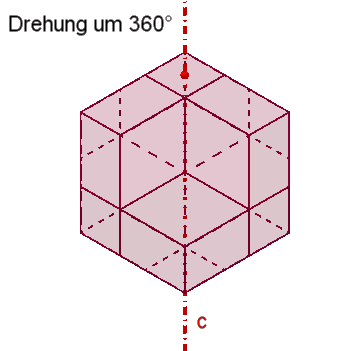
Symmetrie des Rhombendodekaeders:

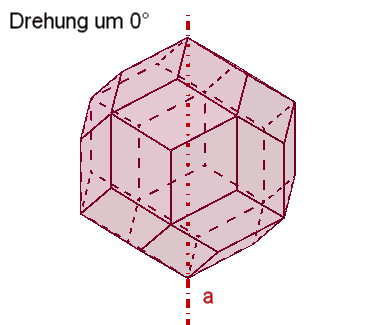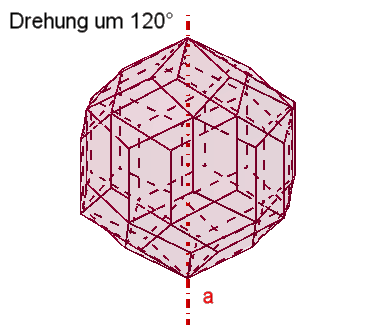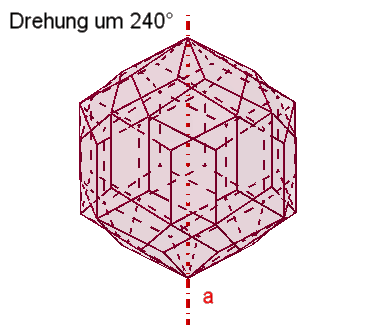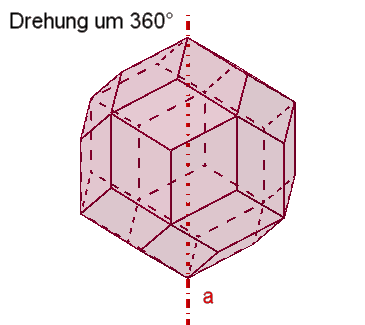
Das Rhombendodekaeder besitzt

3 vierzählige Drehachsen a durch die 6 Pyramidenspitzen,

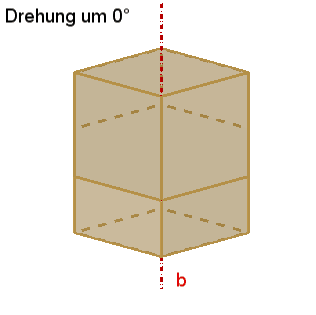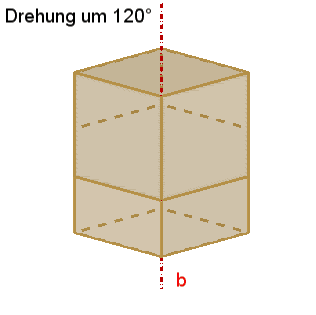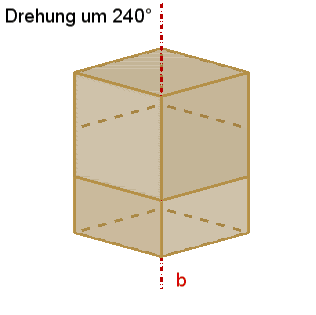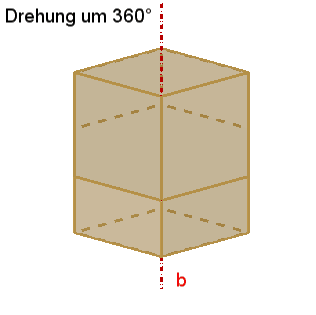
4 dreizählige Drehachsen b durch die 8 Würfelecken,

6 zweizählige Drehachsen c durch die Mitten gegenüberliegender Seitenflächen.

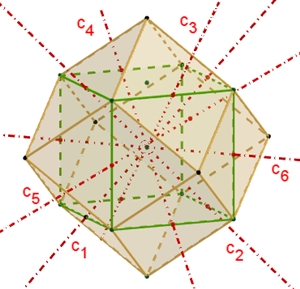
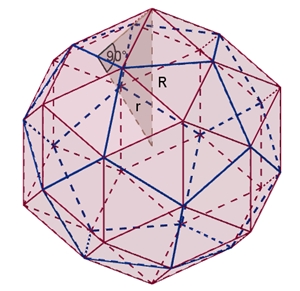
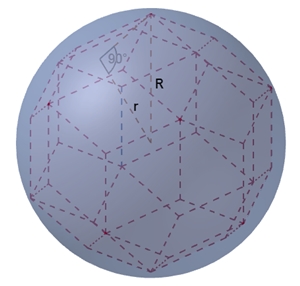
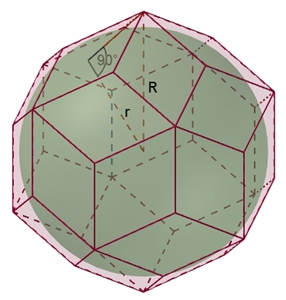
Das Rhombentriakontaeder

Das Rhombentriakontaeder besitzt 30 Rauten, 32 Ecken und 60 Kanten. An 12 der Ecken grenzen 5 Kanten und an die übrigen 20 Ecken grenzen 3 Kanten an. Das Längenverhältnis der Diagonalen der Rauten ist gleich der goldenen Schnittzahl.
Nach Polyedersatz von Euler: 30 + 32 = 60 + 2.

Das Rhombentriakontaeder entsteht durch Aufsetzen gleich großer Pyramiden auf die Seitenflächen (reguläre Fünfecke) eines Dodekaeders.

Die Dodekaederkanten bilden die Diagonale f der Raute mit der Seitenlänge a.

Es gilt: e/f = τ ≈ 1,618
(τ ist goldene Schnittzahl)

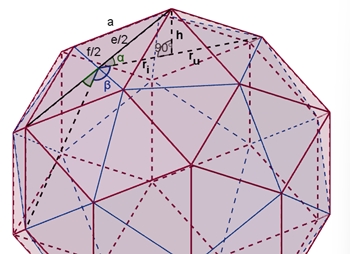
Begründung für e/f = τ

Der Winkel zwischen zwei Seitenflächen des Dodekaeders beträgt β = 180° - arctan(2).

Dann muss für den Winkel α gelten 2 α + β = 180°, damit eine ebene Raute mit den Diagonalen e und f entstehen kann. Dies ist der Fall für e = f/2 (1 + √5).

(f/2)² + (e/2)² = a²  (Pythagoras)
f²/4 + f²/16 (6 + 2√5) = a²  

 f =  a √(50 – 10√5) / 5

 e =  a √(10√5 + 50) / 5

r_i = 1/2 f √(1 + 2/√5) (Inkreisradius des regulären Fünfecks)

cos(α) = r_i / (e/2)

cos(α) = 1/2 f √(1 + 2/√5) / (a √(10√5 + 50) / 10)

cos(α) = 1/10 a √(50 – 10√5) √(1 + 2/√5) / (a √(50 + 10√5) / 10)

cos(α) = 1/10 √(50 + 10√5)

α = 1/2 arctan(1/3) + 22,5° ≈ 31,72°

Der Winkel zwischen zwei Dodekaederflächen beträgt β = 180° – arctan(2) ≈ 116,56°.

2 α + β = 2 (1/2 arctan(1/3) + 22,5°) + 180° – arctan(2) = 180°

Damit ist gezeigt, dass die Raute an der Kante des Dodekaeders nicht abknickt und ein ebenes Viereck ist mit  e = f · τ.

Flächeninhalt A_R der Raute in Abhängigkeit von a:

A_R = e·f / 2 = (1 + √5)/4 f² 

A_R = (1 + √5)/4 (50 – 10√5) / 25 a²

A_R = 2/5 √5 a²

Oberflächeninhalt A des Rhombentriakontaeder: A = 30 A_R = 12√5 a²  ≈ 26,833 a²

Berechnung des Volumeninhalts V des Rhombentriakontaeders:

Volumeninhalt V_P einer aufgesetzten Pyramide:

Flächeninhalt des regulären Fünfecks mit der Kantenlänge f : 

A₅ = f²/4 √(25 + 10√5)

A₅ = a² (50 – 10√5) / 100 √(25 + 10√5)

A₅ = 1/2 √(10 + 2√5) a²

Berechnung der Höhe h und des Volumeninhalts V_P der Pyramide:

h² = (e/2)² – r_i²;  r_i² = 1/4 f ²(1 + 2/√5) = (50 – 10√5) (1 + 2/√5) / 100 a²

h² = a² (50 + 10√5) / 100 –  (50 – 10√5) (1 + 2/√5) / 100 a²

h = √5/5 a

V_P = 1/3 A₅ h = 1/6  √(10 + 2√5) √5/5 a³

V_P = 1/30 √(50 + 10√5) a³

Volumeninhalt des Dodekaeders:

V_D = 1/4 (15 + 7√5) f³

V_D = 1/4 (15 + 7√5) (√(50 – 10√5) / 5)³ a³

V_D = 2/5 √(250 + 110√5) a³

Volumeninhalt des Rhombentriakontaeders:

V = V_D + 12·V_P 

V = 2/5 √(250 + 110√5) a³ + 12/30 √(50 + 10√5) a³ = 4 √(5 + 2√5) ≈ 12,31 a³   

Volumeninhalt V des Rhombentriakontaeders: V = 4 √(5 + 2√5) ≈ 12,311 a³

Berechnung des Radius R der Umkugel des Rhombentriakontaeders:

R = r_i (Dodekaeder) + h

R = f/20 √(250 + 110√5) + √5/5 a

R = a √(50 – 10·√5) / 100 √(250 + 110√5)  + √5/5 a

R = (1 + √5)/2 a

Radius R der Umkugel durch die Pyramidenspitzen R = (1 + √5)/2 a = τ a ≈ 1,618 a

Berechnung des Radius r der Inkugel des Rhombentriakontaeders:

r² = R² – (e/2)²  (Pythagoras)

r² = (6 + 2√5)/4 a² –  (10·√5 + 50) / 100 a²

r² = (2/5 √5 + 1) a²

r = √(25 + 10√5)/5 a ≈ 1,376 a

Radius der Inkugel r = √(25 + 10√5)/5 a ≈ 1,376

Rhombentriakontaeders mit Umkugel und mit Inkugel

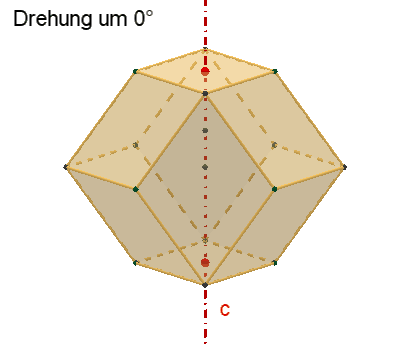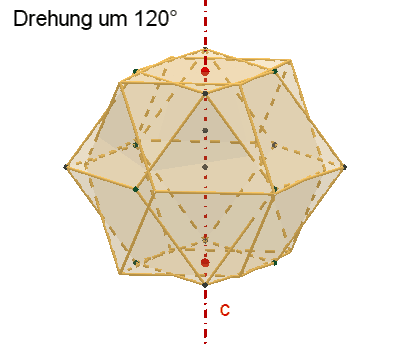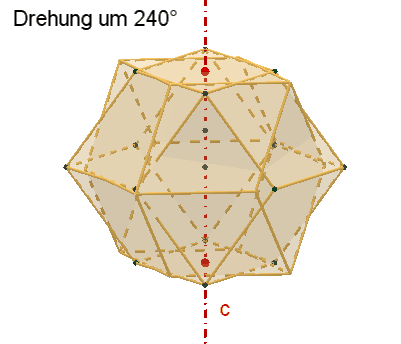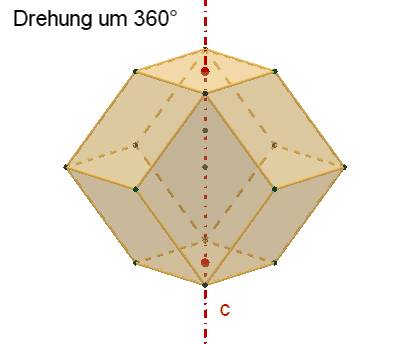
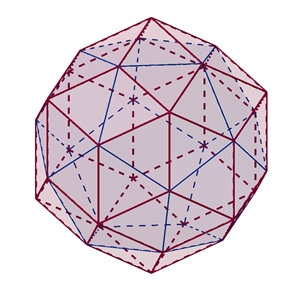
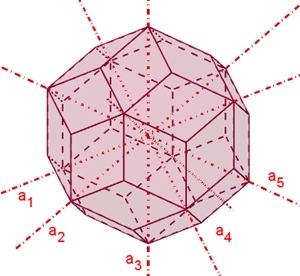
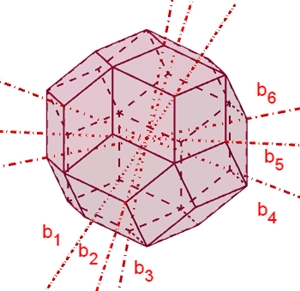
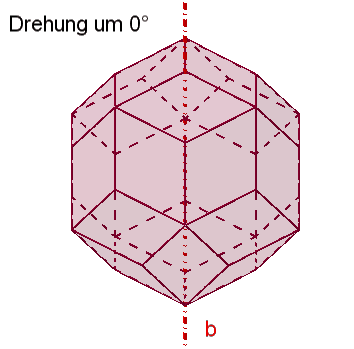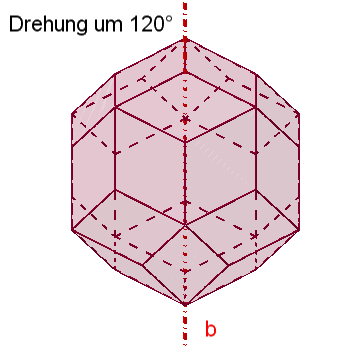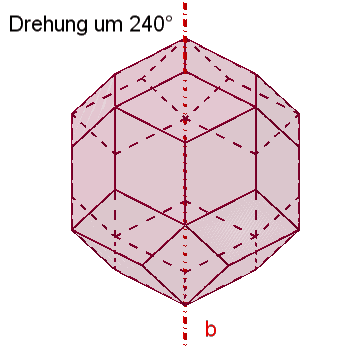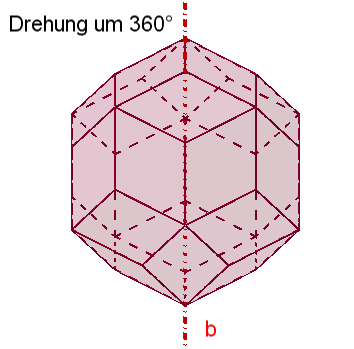
Symmetrie des Rhombentriakontaeders:

Das Rhombentriakontaeder besitzt

5 fünfzählige Drehachsen a durch die 10 Pyramidenspitzen,

6 dreizählige Drehachsen b durch die stumpfen Ecken der Rauten,

15 zweizählige Drehachsen c durch die Mittelpunkte der Rauten.

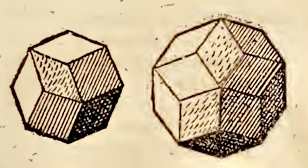
Geschichtliches

Die Polyeder Rhombendodekaeder und Rhombentriakontaeder wurden von Johannes Kepler im II. Buch der Harmonices Mundi (1619) S. 61 beschrieben:
„Vollkommenste räumliche Kongruenzen werden auch gebildet von halbregulären Figuren, nämlich von ebenen Rhomben, und zwar in zwei Fällen.“
(in Deutsch aus dem Lateinischen)

     Zeichnung des Rhombendodekaeders und Rhombentriakontaeders durch J. Kepler.

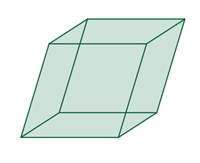
Johannes Kepler hat gezeigt, dass es nur diese zwei Rhomben-Polyeder gibt, wenn man den Würfel und das Rhomboeder nicht dazurechnet. Das Rhomboeder ist ein Polyeder, das von sechs kongruenten Rauten begrenzt wird.

               Würfel                               Rhomboeder