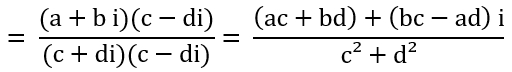Die komplexen Zahlen

Die komplexen Zahlen wurden als Erweiterung der reellen Zahlen eingeführt, um die Gleichung x² = – 1 lösbar zu machen.
Dazu wird die imaginäre Einheit i eingeführt, für die gilt: i² = – 1.

Kartesische Form der komplexen Zahl z:

z = a + b٠i,  kurz z = a + b i, i² = – 1, mit dem Realteil a und dem Imaginärteil b, a und b sind reelle Zahlen.

Polarform der komplexen Zahl z:

z = r٠(cos(φ) + i٠sin(φ)) = r٠e ^iφ, e = 2,7182818… Eulersche Zahl

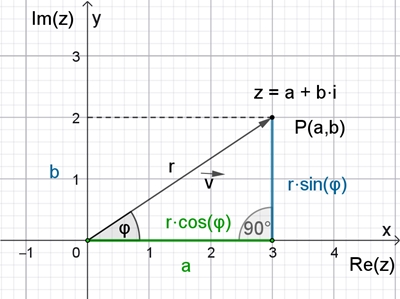
Anschauliche Darstellung von z in einer (komplexen) Ebene

Die komplexe Ebene kann einem kartesischen Koordinatensystem zugeordnet werden. Dann entspricht der komplexen Zahl z = a + b i der Punkt P(a,b) oder der Ortsvektor .

Addition und Subtraktion von komplexen Zahlen z = a + b i und w = c + d i

z + w = (a + b i) + (c + d i) = (a + c) + (b + d) i

z – w = (a + b i) – (c + d  i) = (a – c) + (b – d) i 

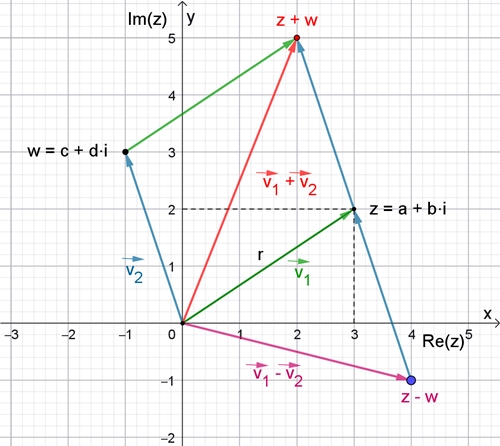
Anschauliche Darstellung der Addition und Subtraktion in der Ebene

Die Addition bzw. Subtraktion von komplexen Zahlen kann auch mit Hilfe der Vektoraddition bzw. Vektorsubtraktion dargestellt werden.

Multiplikation komplexer Zahlen mit i² = – 1

In Koordinatenform:

z ٠ w = (a + b i)٠ (c + d  i) = a c + a d i + b c i + b d i² = (a c  – b d) + (a d + b c) i

In Polarform mit z = r e ^iα und w = s e ^iβ :

z٠ w = r٠ s ٠  e ^i(α+β)

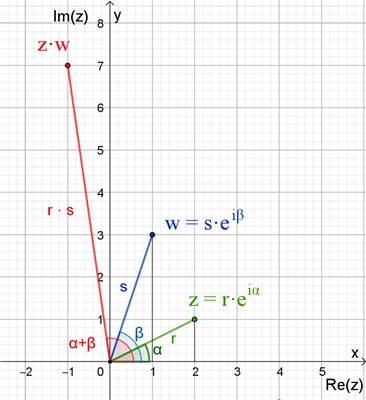
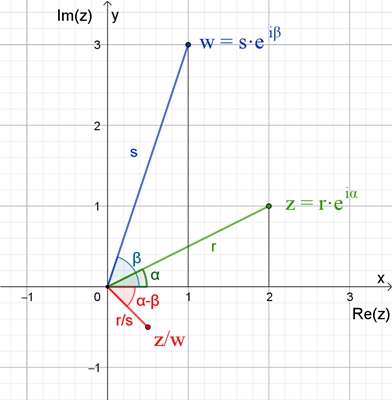
Anschauliche Darstellung der Multiplikation in der Ebene

Division komplexer Zahlen mit i² = – 1

In Koordinatenform:

z / w = (a + b i) / (c + d i) =

In Polarform mit z = r e ^iα und w = s e ^iβ

z / w = r / s ٠  e ^i(α–β)

Anschauliche Darstellung der Division in der Ebene

Gesetze

Kommutativgesetz, Assoziativgesetz und Distributivgesetz gelten auch für die komplexen Zahlen.

Das Kommutativgesetz
der Addition:  z₁ + z₂ = z₂ + z₁, der Multiplikation:  z₁ ٠ z₂ = z₂ ٠ z₁

Das Assoziativgesetz
der Addition:  z₁ + (z₂ + z₃) = (z₁ + z₂) + z₃, der Multiplikation: :  z₁ ٠ (z₂ ٠ z₃) = (z₁ ٠ z₂) ٠ z₃

Das Distributivgesetz
z₁ ٠ (z₂ + z₃) = z₁ ٠ z₂  + z₁ ٠ z₃

Zu jeder Zahl z = a + b i gibt es eine Zahl –z = – a – b i, mit z + (–z) = 0.

Zu jeder Zahl z = a + b i gibt es eine Zahl 1 / z = 1 / (a + b i) = (a – b i) / (a² + b²), wobei gilt:
z ٠ (1/z) = 1.

Mit diesen Eigenschaften ist die Menge ℂ der komplexen Zahlen ein Körper, da folgende Bedingungen erfüllt sind:

(ℂ, +) ist eine kommutative Gruppe mit dem neutralen Element 0.

(ℂ, ٠) ist eine kommutative Gruppe mit dem neutralen Element 1.

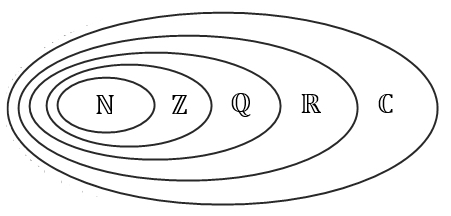
Die Menge ℂ mit Teilmengen

Mengendiagramm:

ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ  (⊂ : „ist echte Teilmenge von“)

ℕ = Menge der natürlichen Zahlen = {1, 2, 3, . . . }

ℤ = Menge der ganzen Zahlen = { . . . –3, –2 –1, 0 ,1, 2, 3, . . . }

ℚ = Menge der rationalen Zahlen = Menge aller Brüche von ganzen Zahlen

ℝ = Menge der reellen Zahlen = Menge aller Brüche und Wurzeln

ℂ = Menge der komplexen Zahlen

Die Mengen ℚ und ℝ stellen ebenfalls einen Körper dar.

Reelle Zahlen können geordnet werden, komplexe Zahlen jedoch nicht.

Anwendungen

Komplexe Zahlen werden oft benutzt, um Schwingungen und Wellen in der Physik und Elektrotechnik zu beschreiben.

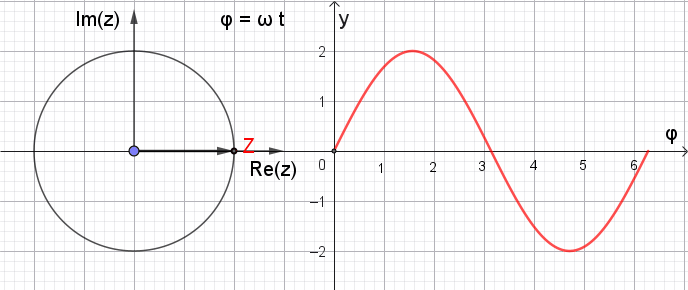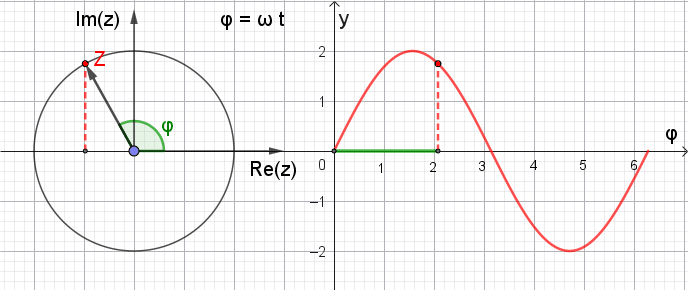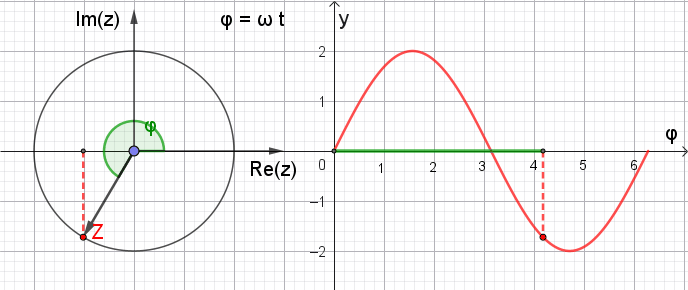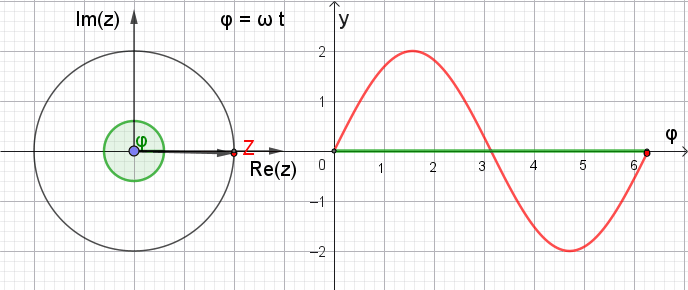
In einem Zeigerdiagramm kann eine harmonische Schwingung (Sinusschwingung) durch einen mit der Kreisfrequenz ωω um den Nullpunkt rotierenden Zeiger in der komplexen Ebene dargestellt werden, dessen Länge die Amplitude repräsentiert.

Zeigerdiagramm mit variablem φ

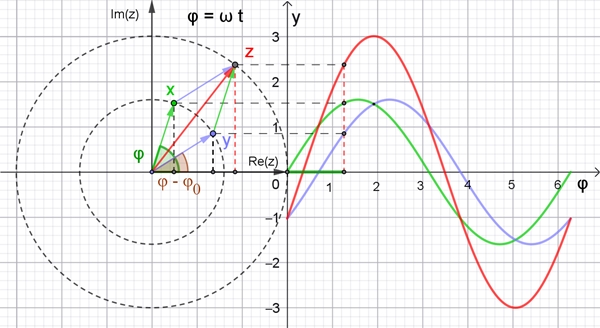
Zeigerdiagramm mit einer zusätzlich um φ₀ phasenverschobenen Sinusschwingung und der Überlagerung der beiden Sinusschwingungen

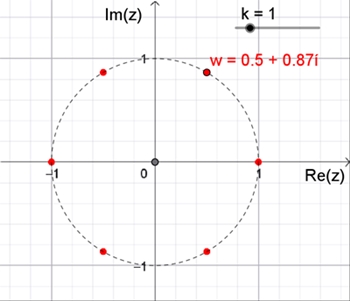
Die nnnn-ten Einheitswurzeln lassen sich in der komplexen Zahlenebene geometrisch anschaulich interpretieren: Sie sind die auf dem Einheitskreis (mit Mittelpunkt 0 und Radius 1) liegenden Ecken eines regelmäßigen nn-Ecks, wobei eine der Ecken die Zahl 11 ist, denn diese ist für jedes n≥1 n≥1 eine nn-te Einheitswurzel.

Beispiel: w = e ^{i 2πk / n} , n = 6, k ∊ {0, 1, 2, 3, 4, 5}

Komplexe Zahlen werden bei der Berechnung und Darstellung von Fraktalen verwendet, z.B. bei der Mandelbrotmenge.