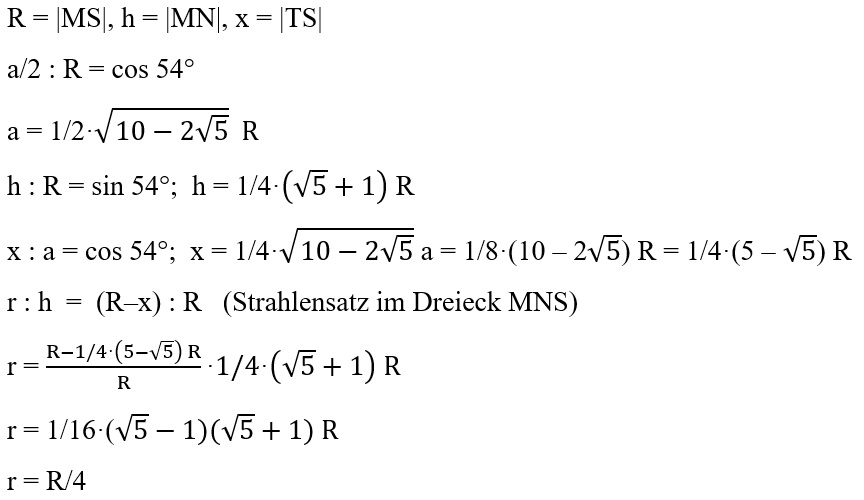|
Kreis und Vieleck 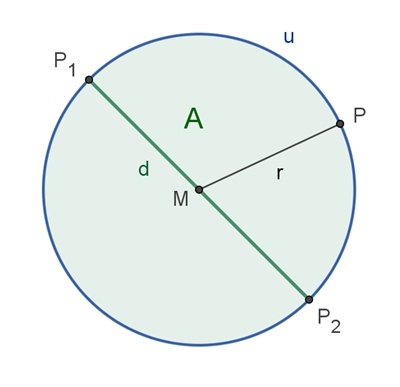
Der Kreis (Kreislinie) k ist die
Menge aller Punkte P einer Ebene, die von einem festen Punkt M (Mittelpunkt)
den gleichen Abstand r (Radius) haben, i.Z.
k = {P | |MP| = r}.
Mit einem Zirkel kann man die Kreislinie zeichnen.
Durchmesser d = 2٠r = 2 r
Die Kreisfläche ohne Kreislinie
heißt offene Kreisfläche, die Kreisfläche mit Kreislinie heißt
abgeschlossene Kreisfläche.
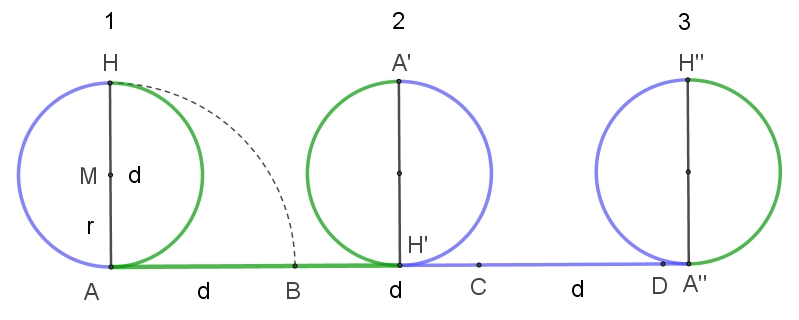
Wenn ein Kreis einmal abrollt, hat er eine Wegstrecke zurückgelegt, die
seinem Umfang entspricht und etwas länger als das Dreifache seines
Durchmessers ist. Der Faktor mit dem die Länge d des Durchmessers
multipliziert wird, um die Länge
u des Kreisumfangs zu erhalten,
wird als Kreiszahl π (pi) bezeichnet.
u = d٠π =
2 r π, π ≈ 3,1415926536 (auf 10 Nachkommastellen)
Flächeninhalt A
des Kreises:
A = r²
π
Begründung:
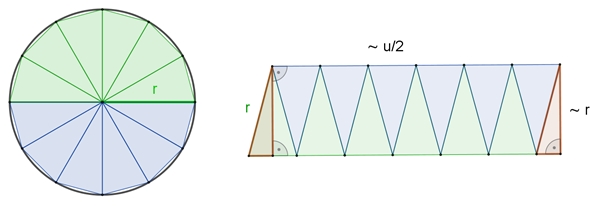
Die Kreisfläche wird durch ein eingepasstes reguläres n-Eck (n gerade
natürliche Zahl) in gleich große Dreiecke unterteilt und passend zu einem
Rechteck zusammengesetzt. Je größer die Eckenzahl n ist, umso mehr nähert
sich die Rechtecklänge dem halben Umfang u/2 an und die Rechteckbreite dem
Radius r an.
Kreisflächeninhalt A = u/2٠r = 2rπ : 2٠r
= r²π
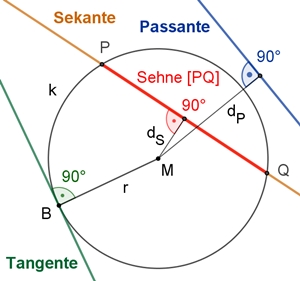
M ist der Mittelpunkt des Kreises k.
Die Passante hat keinen Punkt mit dem Kreis gemeinsam. Der
Abstand dP der Passante von M ist größer als r.
Die Sekante schneidet den Kreis in zwei Punkten P und Q.
Die Strecke [PQ] heißt Sehne. Der Abstand dS der Sekante oder
Sehne von M ist kleiner als r.
Die Tangente berührt den Kreis im Punkt B. Der Abstand der
Tangente von M ist gleich r.
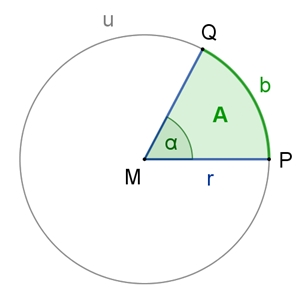
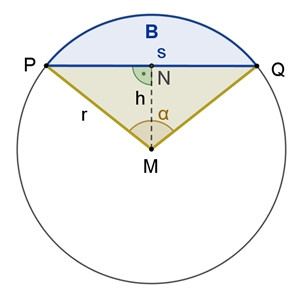
Der Kreissektor
Es gelten
folgende Proportionen mit u = 2rπ und Mittelpunktswinkel α im Gradmaß:
Daraus
folgt:
N ist der Mittelpunkt der Kreissehne [PQ] und s = |PQ|.
Im Dreieck MPN gilt:
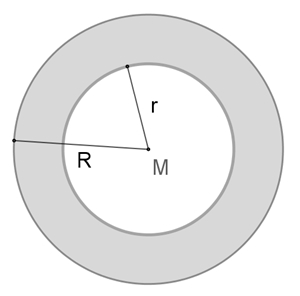
Flächeninhalt des
Kreisrings:
R²
π – r² π = (R² – r²) π
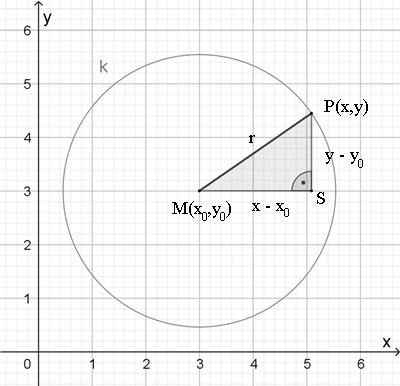
Koordinatengleichung
Für den Abstand r des Punktes P(x,y) vom Punkt M(x0,y0)
gilt:
(x – x0)² + (y – y0)² = r²
(Pythagoras im ΔMSP)
Spezialfall:
Einheitskreis
x² + y² = 1 mit M(0,0) und r = 1
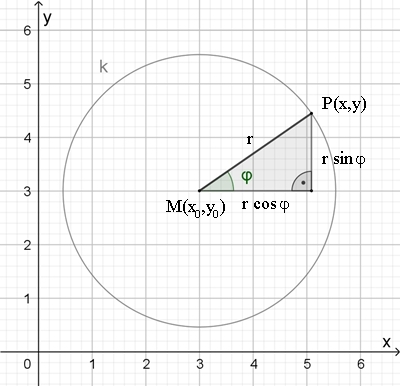
Parametergleichungen
x = x0 + r cos φ
0 ≤ φ ≤ 2 π
Geometrische Sätze zum Kreis
Umkreis und Inkreis des Dreiecks
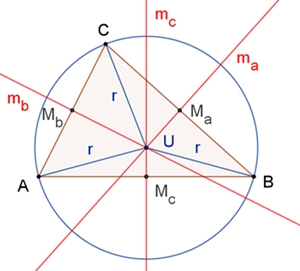
Satz von den
Mittelsenkrechten im Dreieck
Die drei Mittelsenkrechten der
drei Seiten eines Dreiecks schneiden sich in einem Punkt, dem Umkreismittelpunkt
U des Dreiecks.
Begründung s.
Lehrsätze im Dreieck
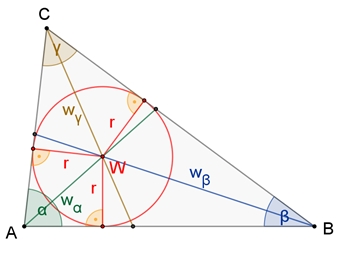
Satz von den
Winkelhalbierenden im Dreieck
Die drei Winkelhalbierenden der
drei Winkel eines Dreiecks schneiden sich in einem Punkt, dem Inkreismittelpunkt
W des Dreiecks.
Begründung s. Lehrsätze im Dreieck
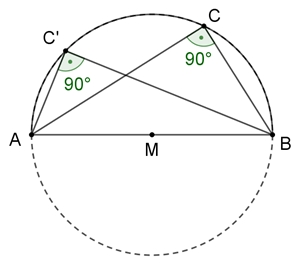
Satz des Thales
Ein Dreieck ABC hat genau dann bei C einen rechten Winkel, wenn die Ecke C
auf dem Halbkreis über [AB] liegt.
Begründung s. Lehrsätze im Dreieck
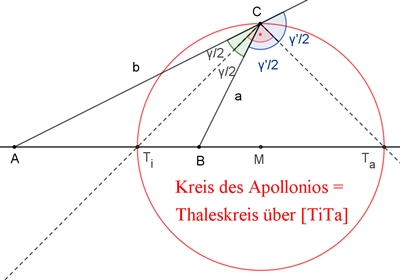
Der Apollonioskreis
Alle Punkte C, deren Entfernungen von zwei gegebenen Punkten A und B ein
festes Verhältnis b : a haben, liegen auf einem Kreis mit Durchmesser [TiTa].
Begründung:
wγ
und wγ‘ sind die Winkelhalbierenden zu
γ
und dem Nebenwinkel
γ‘ zu
γ,
wobei gilt:
Mit den parallelen Geraden TiC, BD und BE, TaC folgt unter zweimaliger
Anwendung der zentrischen Streckung mit Zentrum A:
Da
≮TiCTa
= 90° gilt, liegt C auf dem Thaleskreis über [TiTa].
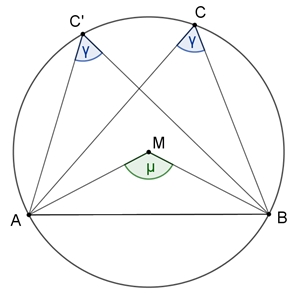
Umfangswinkel-Satz
Alle Umfangswinkel
γ
=
≮ACB
über derselben Sehne [AB] eines Kreises sind gleich groß.
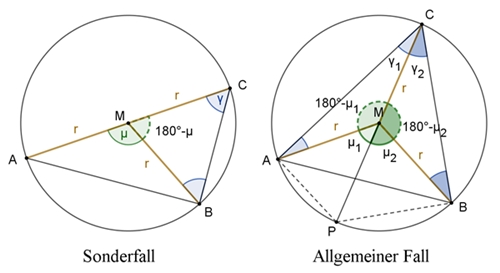
Mittelpunktswinkel-Satz
Liegen Umfangs- und
Mittelpunktswinkel auf derselben Seite einer Sehne [AB], so ist der
Mittelpunktswinkel doppelt so groß wie der Umfangswinkel.
S
Begründung:
Im Sonderfall gilt:
Im allgemeinen Fall gilt:
180°– μ1
+ 2γ1
= 180°
180°– μ2
+ 2γ2
= 180° μ = μ1 + μ2 = 2γ1 + 2γ2 = 2γ
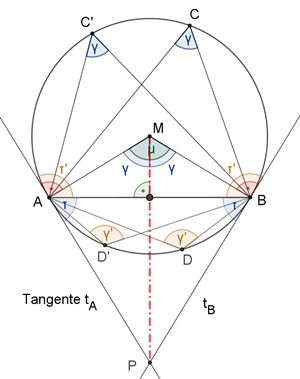
Sehnen-Tangenten-Winkel
Der Sehnen-Tangenten-Winkel τ
=
≮PAB ist halb so groß wie der zur
Sehne [AB] gehörige Mittelpunktswinkel μ und genau so groß wie der
Umfangswinkel
γ.
Die Umfangswinkel auf verschiedenen Seiten einer Sehne ergänzen sich zu
180°, da sich die zugehörigen Sehnen-Tangenten-Winkel τ
und
τ‘ zu 180° ergänzen.
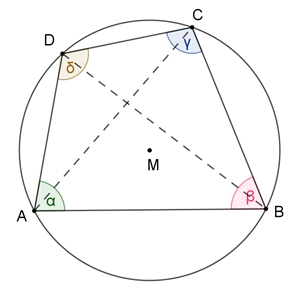
Sehnenviereck
Ein Viereck ist genau dann ein
Sehnenviereck, wenn sich gegenüberliegende Winkel zu 180° ergänzen, d.h.
wenn gilt:
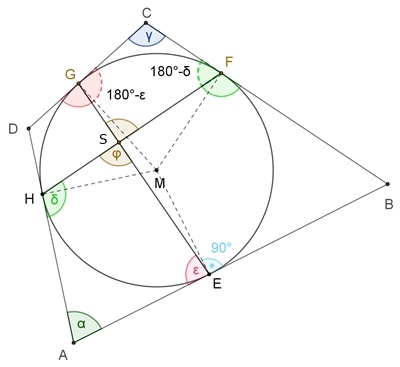
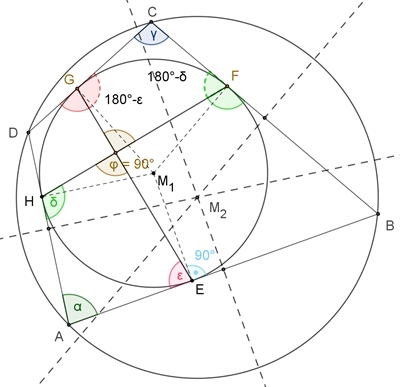
Sehnen-Tangenten-Viereck
Falls sich die Sehnen der gegenüberliegenden Berührpunkte des
Tangentenvierecks im rechten Winkel φ = 90° schneiden gilt:
Begründung:
I + II α +
γ + 180° = 360°
Entsprechend gilt: β + δ = 180°
Damit
entsteht ein Sehnen-Tangenten-Viereck,
d.h. das Viereck ABCD ist sowohl
Sehnenviereck als auch Tangentenviereck und besitzt einen Inkreis und einen
Umkreis.
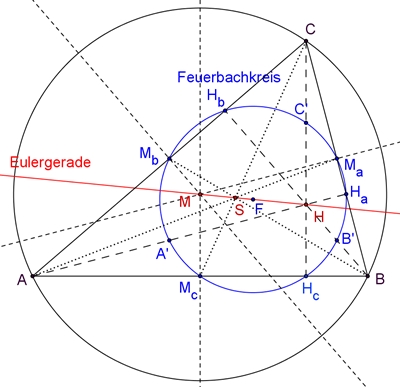
Feuerbachkreis und Eulergerade
Die Seitenmitten Ma, Mb,
Mc und die Höhenfußpunkte Ha, Hb, Hc eines
Dreiecks und die Mittelpunkte A’, B’, C’ zwischen den Dreiecksecken und dem
Höhenschnittpunkt liegen auf einem Kreis. Dieser Kreis heißt
Feuerbach-Kreis oder
Neunpunktekreis mit Mittelpunkt F.
Weitere Eigenschaften:
1. Die Eulersche Gerade geht auch durch den Mittelpunkt F des
Feuerbach-Kreises;
2. Die vier Punkte M, S, F und H sind vier harmonische Punkte mit dem
Teilverhältnis
3. Im Dreieck ABC besitzt der Feuerbach-Kreis einen halb so großen Radius
wie der
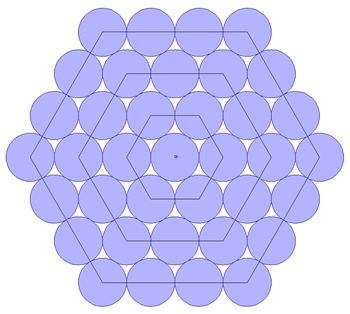
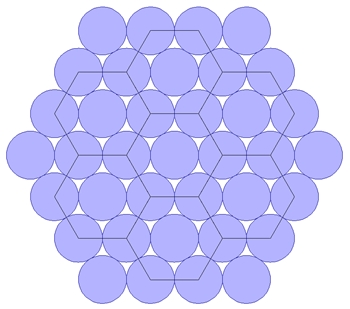
Die Mittelpunkte sich berührender Kreise sind Eckpunkte regulärer Sechsecke.
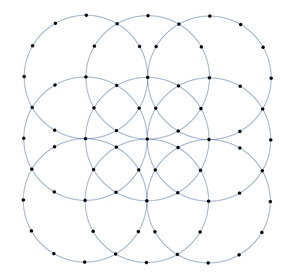
Der 12-Punkte-Kreis
Kreise in dieser Anordnung schneiden sich in
12 Punkten, die auf einem Kreis gleichen Abstand besitzen und damit die
Eckpunkte eines regelmäßigen Zwölfecks darstellen.
Ausgewählte
Konstruktionen an Kreisen Kreismittelpunkt konstruieren:
Die Mittelsenkrechten zweier Kreissehnen schneiden sich im Mittelpunkt M.
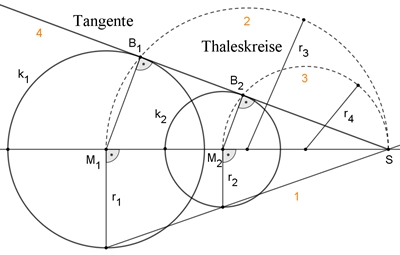
Tangente an zwei verschieden große Kreise konstruieren:
Die Ziffern 1 bis 4 geben die Reihenfolge der Konstruktion an.
Es gibt eine zu M1M2 spiegelbildlich liegende zweite
Tangente.
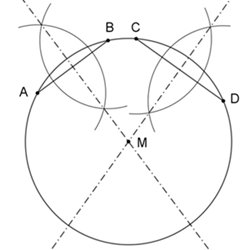
Konstruktion eines regulären Sechsecks:
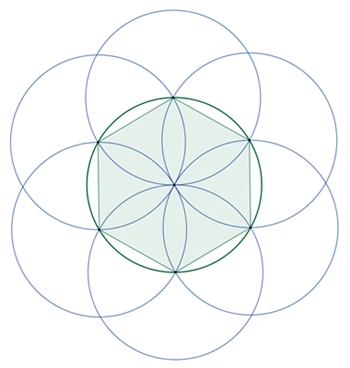
Die Mittelpunkte von 6 Kreisen, die auf einem gegebenen Kreis mit Radius r
den gleichen Abstand r haben, sind die Eckpunkte eines regulären Sechsecks.
Alle 7 Kreise haben damit den gleichen Radius r, der gleich der Seitenlänge
des regulären Sechsecks ist.
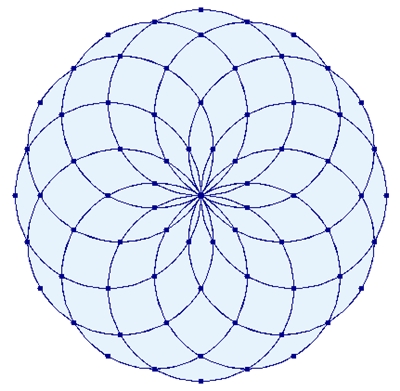
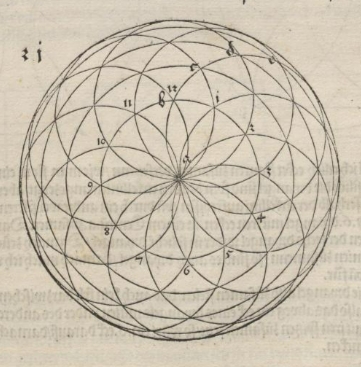
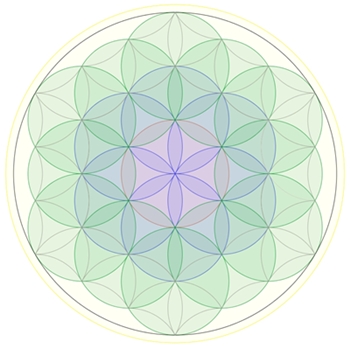
Mandala aus einer Reihe von derartig sich schneidenden Kreisen gebildet.
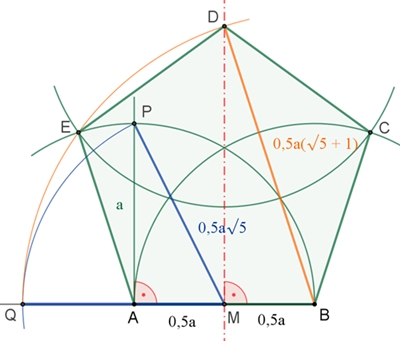
Konstruktion eines regulären Fünfecks mit gegebener Seite [AB] der Länge a:
P liegt:
Q liegt:
E liegt:
D liegt:
C liegt:
Es entsteht ein reguläres Fünfeck ABCDE, in dem die gleich langen Diagonalen
d im goldenen Schnitt zur Seitenlänge a stehen,
d : a = (√5 + 1)/2 : 1.
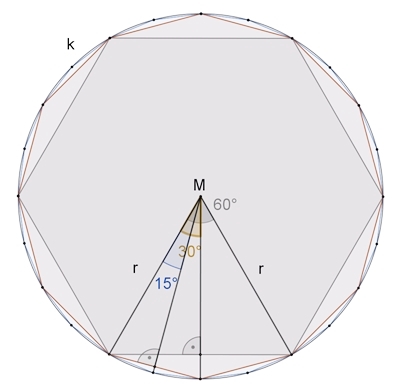
Annäherung des Kreises durch Vielecke
Näherung des Kreises durch ein reguläres 6-eck, 12-eck, 24-eck, 48-eck, …
liefert folgende Flächenberechnungen A6, A12, A24,
A48, …:
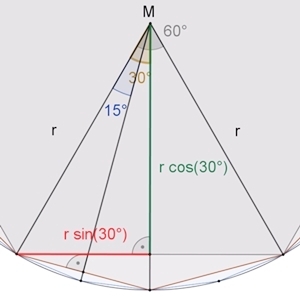
A6: 6٠1/2٠2٠r
sin(30°)٠r cos(30°)
≈ 2,60 r²
Die regulären Vielecke nähern sich mit zunehmender Eckenzahl dem
Flächeninhalt
π r² an. Es
gilt:
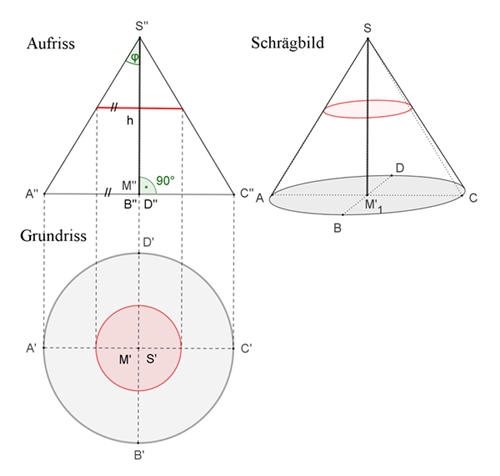
Der Kreis als Schnittfläche des geraden Kreiskegels mit einer zur Grundfläche parallelen Ebene im Grundriss, Aufriss und Schrägbild
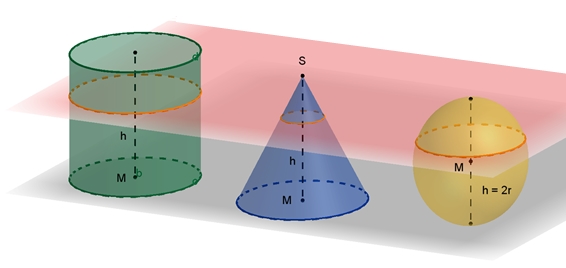
Kreise als Schnittflächen einer zur Grundebene parallelen Fläche mit Zylinder, Kegel und Kugel in Schrägbilddarstellung
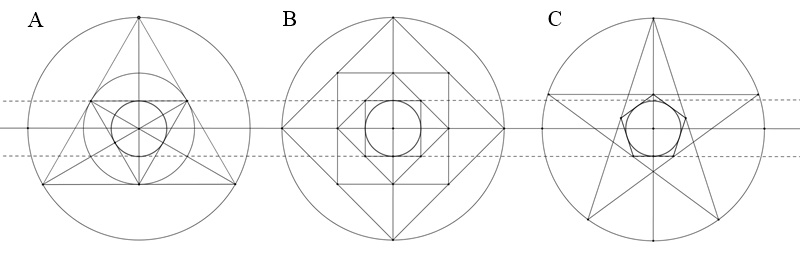
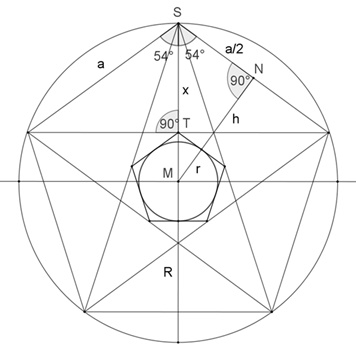
Umkreise und spezielle Inkreise von
regelmäßigem Dreieck, Viereck und Fünfeck
Bei gleich großem Umkreisradius R
ergeben sich in den Figuren gleich große Inkreise mit Radius r = R/4
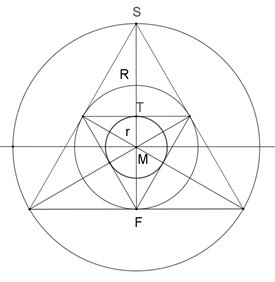
Der Höhenschnittpunkt im gleichseitigen Dreieck teilt die Höhe im Verhältnis
2:1.
Daraus folgt: |MF| = R/2
Im kleinen gleichseitigen Dreieck gilt dann entsprechend:
r = |MT| = 1/2⸱R/2 = R/4
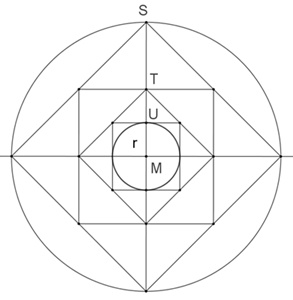
Begründung für B:
T ist der Mittelpunkt der Strecke MS und U
ist der Mittelpunkt der Strecke MT.
Daraus folgt: r = R/4
Foto von einem Teil der Fassade des
Kulturzentrums CNAD
in Mindelo, Kapverden. Jedem Farbton ist eine Note von c bis h zugeordnet
bzw. drückt einen Akkord, Rhythmus, Bass, Drums oder Pause aus. Die Musik
dazu ist vom kapverdischen Komponisten und Musiker Vasco Martins komponiert:
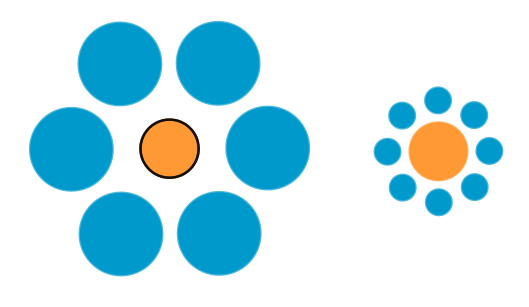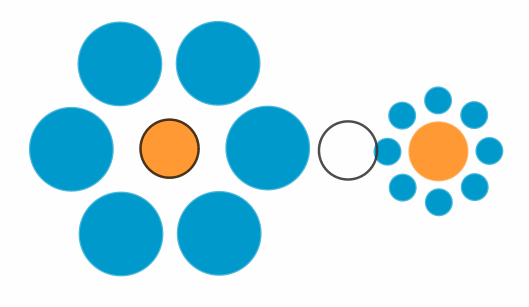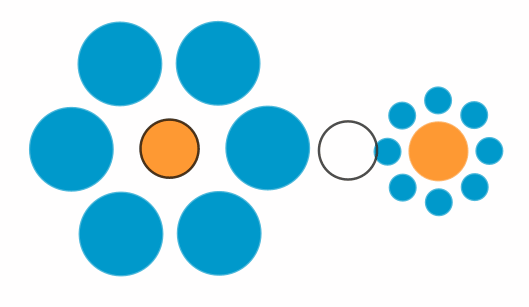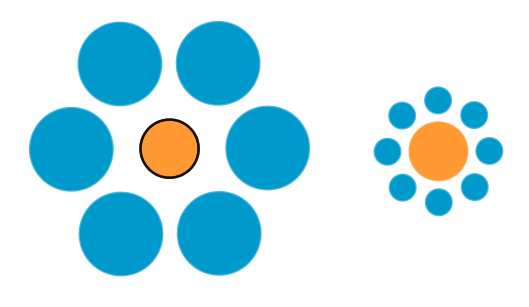
Optische Täuschungen mit Kreisen
oder Kreisbögen
Der linke orange Kreis ist genau so groß wie
der rechte (Ebbinghaus-Täuschung,
ca, 1890 entdeckt durch den Psychologen Hermann Ebbinghaus)
Der innere graue Kreisflächeninhalt ist genau so groß wie der Flächeninhalt
des äußeren gauen Kreisrings, wobei die Kreisringe gleichen Abstand r haben.
Kreisflächeninhalt innen: 9 r²
π
(Bullaugen-Illusion)
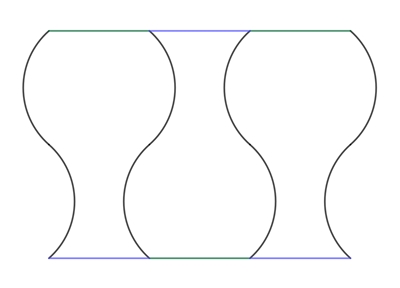
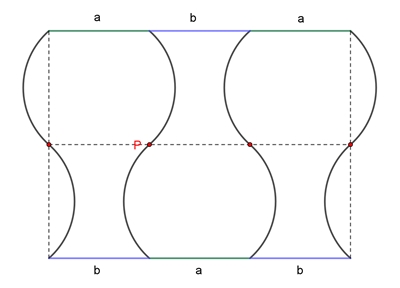
Die drei Vasenformen sind zueinander kongruent. Die mittlere Vasenform ist
die am Punkt P gespiegelte linke Vasenform. Die Kreisbögen sind an den roten
Punkten punktsymmetrisch, die Vasenformen sind achsensymmetrisch.
Es gilt: 2a + b = 2b + a
Daraus folgt: a = b
Die 6 farbig eingezeichneten Strecken sind gleich lang (1855 entdeckt durch
Johann J. Oppel)
Im linken Bild scheint man einen Kreis zu sehen, der im rechten Bild
eingezeichnet ist. (Kanizsa Wahrnehmungstäuschung, veröffentlicht durch
Gaetano Kanizsa
1979 in Form eines Dreiecks, sog.
Kanizsa-Dreieck).
Die meisten Menschen sehen im linken Bild nur
Rechtecke. Im rechten Bild sind die darin versteckten Kreise hervorgehoben.
Nach Betrachtung des rechten Bildes sieht man auch im linken Bild Kreise
(Coffer-Illusion,
Anthony
Norcia 2006)
In Erinnerung an den französischen Maler
Kunstvolle geometrische Form eines
Zurück Zurück zur Startseite |