|
Keplerscher Dodekaeder- und Ikosaederstern
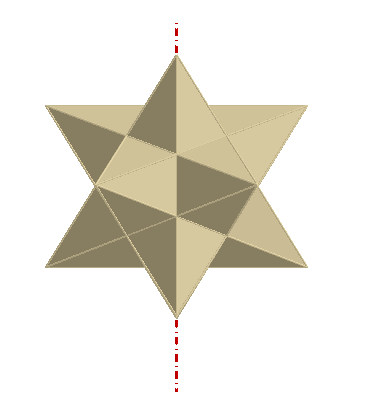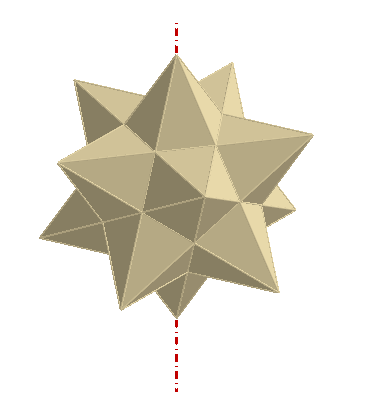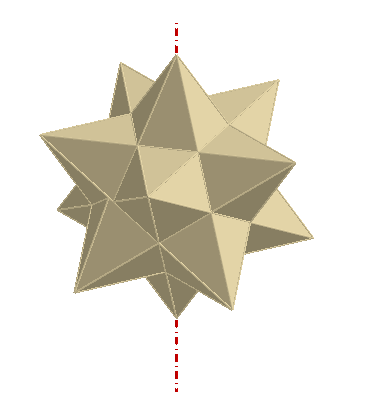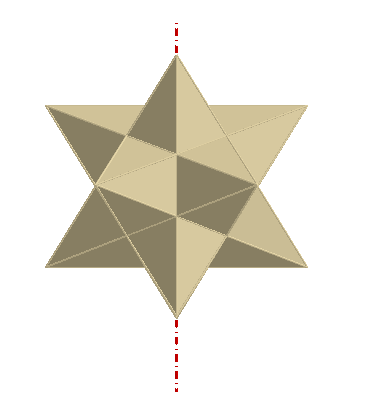
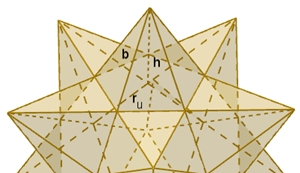
Der Dodekaederstern 
Johannes Kepler
(1571 – 1630) hat diesen Stern in seinem II. Buch der
Harmonices Mundi
1619 beschrieben. Der Stern besteht aus einem
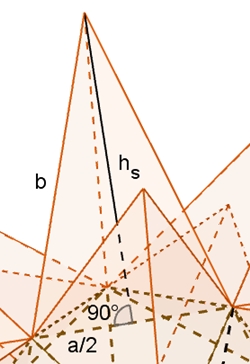
Dodekaeder, dem 12 fünfseitige Pyramiden aufgesetzt sind, wie nebenstehend zu sehen ist. Die Kantenlänge des Dodekaeders sei a.
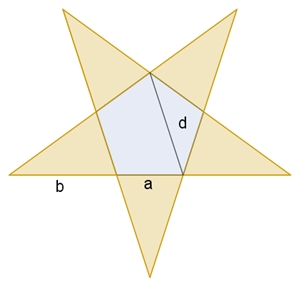
Berechnung von b
mit d = a (1 +
√5)
/ 2 = a
τ
(goldene Schnittzahl):
(a + b) / b = d
/ a (Strahlensatz)
a/b = d/a – 1
b = a² / (d – a)
und d eingesetzt ergibt:
b = a / ((1 +
√5)/2 – 1)
b = a (1 +
√5) / 2 =
a
τ
Berechnung der
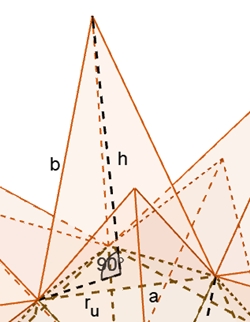
Höhe h der aufgesetzten Pyramide:
h² = b² – ru² (Pythagoras);
ru
= a/10
√(50 + 10√5) (ru
=
Radius des Umkreises des regulären Fünfecks)
h² = a² (6 + 2√5) / 4 – a²/100
(50 + 10√5)
h² = a² ( 1 +
2/5
√5)
h = a/5
√(25 + 10√5)
Berechnung des
Pyramidenvolumens VP:
VP = 1/3 A5 h;
A5
= a²/4
√(25 + 10√5)
(Flächeninhalt des regulären Fünfecks) VP = a²/12 √(25 + 10√5) · a/5 √(25 + 10√5)
VP
= a³/12 (5 + 2√5)
Berechnung des
Volumeninhalts V des Dodekaedersterns:
V = VD + 12 VP;
VD
= 1/4 (15 + 7√5) a³ (Volumeninhalt des Dodekaeders)
V = 1/4 (15 +
7√5) a³ + (5 + 2√5) a³
V = 1/4 (35 + 15√5) a³ ≈
17,14 a³ 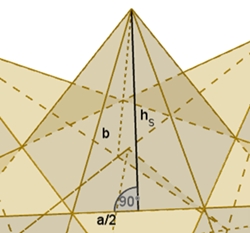
Berechnung des
Oberflächeninhalts O des Dodekaedersterns:
hs² = b² – (a/2)²
hs² = a² (6 + 2√5) / 4 – a² / 4
hs² = a²/4 (5 + 2√5)
hs = a/2
√(5 + 2√5)
Inhalt der
Dreiecksfläche mit Grundlinie a und Höhe hs:
A△
= 1/2 a hs
= a²/4
√(5 + 2√5)
O = 60
· a²/4
√(5 + 2√5)
Oberflächeninhalt O des Dodekaedersterns O = 15
√(5
+ 2√5)
a² ≈ 46,17 a²
Die
Symmetrieeigenschaften des Dodekaedersterns entsprechen den
Symmetrieeigenschaften des
Dodekaeders.
Der
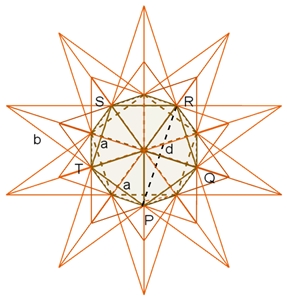
Ikosaeder-Stern 
Johannes Kepler (1571 –
1630) hat diesen Stern in seinem II. Buch der Harmonices Mundi 1619
beschieben. Der Stern besteht aus einem Ikosaeder, dem 20 dreiseitige Pyramiden
aufgesetzt sind, wie nebenstehend zu sehen ist.
Die Kantenlänge des Ikosaeders sei a.
PQRST ist ein
reguläres Fünfeck (s. Ikosaeder) und es ergibt sich wie in obiger Berechnung
für b:
b = a (1 +
√5) / 2 =
a
τ
Berechnung der
Höhe h der aufgesetzten Pyramide:
h² = b² – ru²;
ru
= a/3
√3
(
ru
=
Radius des Umkreises des gleichseitigen Dreiecks)
h² = a² (6 + 2√5) / 4 – a²/ 3
h² = a²/6 (7 + 3√5)
h = a/6 (3√3 +
√15)
Berechnung des
Pyramidenvolumens VP:
VP = 1/3 A3 h;
A3
= a²
√3 /4
(Flächeninhalt des gleichseitigen Dreiecks)
VP = a²
√3 /12
· a/6 (3√3 +
√15)
VP = a³/24 (3 +
√5)
Berechnung des
Volumeninhalts V des Ikosaedersterns:
V = VI + 20 VP;
VI
= 5/12 (3 + √5) a³ (VI
= Volumeninhalt des Ikosaeders)
V = 5/12 (3
+ √5) a³ + 20· a³/24 (3 +
√5)
V = 1/4 (15 + 5√5) a³ ≈
6,55 a³
Berechnung des
Oberflächeninhalts O des Ikosaedersterns:
hs² = b² – (a/2)²
hs² = a² (6 + 2√5) / 4 – a²/4
hs² = a² (5 + 2√5)/4
hs = a/2
√(5 + 2√5)
Inhalt der
Dreiecksfläche mit Grundlinie a und Höhe hS:
A△
= 1/2 a hs
= a²/4
√(5
+ 2√5)
O = 60
· a²/4
√(5 + 2√5)
Oberflächeninhalt O des Ikosaedersterns O = 15
√(5
+ 2√5)
a² ≈ 46,17 a²
Die
Symmetrieeigenschaften des Ikosaedersterns entsprechen den
Symmetrieeigenschaften des
Ikosaeders.
Bemerkungen:
Die Kantenlängen
von der Spitze zum Polyeder sind jeweils das
τ-fache
der Kantenlänge des Polyeders. Der Oberflächeninhalt des Dodekaedersterns ist gleich dem Oberflächeninhalt des Ikosaedersterns.
Die 12 Zacken
des Dodekaedersterns bilden die 12 Eckpunkte eines Ikosaeders und die 20
Zacken des Ikosaedersterns bilden die 20 Eckpunkte eines
Dodekaeders.
|